机器学习笔记——从手写数字识别开始
文章目录
- 前言
-
- 关于这篇博客(预计八月下旬全部完成)
- 关于项目实现
- 监督学习
-
- ANN全连接神经网络的实现
-
- 1.总述
- 2.初始化
- 3.传播及损失
- 4.反向传播
- 决策树以及随机森林的实现
-
- 1.总述
- 2.单棵决策树的实现
- 3.随机森林的实现
- PCA(SVD)主成分分析+自适应距离度量+KNN近邻算法的实现
-
- 1.总述
- 2.PCA主成分分析
- 3.KNN近邻算法
- 4.自适应距离度量
- CNN卷积神经网络的实现
-
- 1.总论
- 2.卷积层
- 3.激励层
- 4.池化层
- 5.全连接层(接ANN或者DNN)
- 6.反向传播
-
- 1.反池化
- 2.反卷积
- SVM支持向量机的实现
- 朴素贝叶斯的实现
-
- 1.总论
- 2.视作连续型数值预处理以及先验概率计算(效果较差)
- 3.视作离散型数值预处理以及先验概率计算
- 无监督学习
-
- K-means聚类的实现
-
- 1.总论
- 2.K-means的实现
- 分析总结及一些思考
-
- 手写数字识别的总结
- 一些感想
前言
- Ozymandias
Percy Bysshe Shelley
I met a traveller from an antique land
Who said: Two vast and trunkless legs of stone
Stand in the desert. Near them, on the sand,
Half sunk, a shattered visage lies, whose frown,
And wrinkled lip, and sneer of cold command,
Tell that its sculptor well those passions read
Which yet survive, stamped on these lifeless things,
The hand that mocked them and the heart that fed:
And on the pedestal these words appear:
‘My name is Ozymandias, king of kings:
Look on my works, ye Mighty, and despair!’
Nothing beside remains. Round the decay
Of that colossal wreck, boundless and bare
The lone and level sands stretch far away.
——盖世功业,皆归尘土。然而我们依然为了现世的梦想奋斗!
关于这篇博客(预计八月下旬全部完成)
这是作者人生中第一篇博客,作为初学者将自己大一下学期进行的机器学习的学习内容进行一个简单的整理,不可避免有很多知识上的错误以及疏漏。作者同时尝试使用多种方法实现手写minst数字识别项目。本文仅供参考,不建议学习。
作者自2021年4月,根据本校一位老师的学习指导,至7月假期,课余进行了一些基本机器学习算法的学习,从最基础的线性回归开始,直至后续的随机决策森林,朴素贝叶斯以及简单的CNN等。由于均系课余时间学习,算法的学习与实现并不系统,更多还是以简单了解为目的。对于每种算法的数学原理也尝试进行了理解,然而其中疏漏固然也不可避免。对于每一种算法,尽量采取了了解的态度,即不进行算法优化更深层次的研究,而是注重基础代码的实现,以及基本原理的理解。本文略去了一些基本的梯度下降等内容,主要对比已经学习的几种机器学习算法(包括最基本的DNN、CNN)对于minst手写数字识别的学习效果。部分模型明显不适合于手写数字识别的实现(根据我目前的理解)但是我仍然使用它们进行了同样的操作。
小学时代有一篇被《达芬奇画鸡蛋》的课文(此处不考虑故事的真实性),这种多个观察角度、多种绘画方法、多次对同一个事件进行尝试的方法,对于知识的掌握有着一定的功效。希望以这种“达芬奇画鸡蛋式精神”,凭借自己的兴趣,来完成这样一件我认为有意义的事情。
关于项目实现
关于代码实现部分,由于作者在最开始的几种算法实现部分,就读于大一,仅仅有少许高中竞赛经历,没有进行系统的python学习,所以部分算法仍然使用了具备OI风格的C++代码进行实现,后期假期完成的算法使用python实现。并且根据我怂恿某同学刚刚开始进行学习,就向老师询问实验室搭建框架类型而被他的导师批评“急于求成”、“浮躁”的经历,在python实现部分代码时,初学阶段不使用pytorch、TensorFlow等框架进行编写,尽量在底层也使用自己编写的框架。
关于minst经典手写数字数据集,MNIST是一个手写体数字的图片数据集,该数据集来由美国国家标准与技术研究所(National Institute of Standards and Technology (NIST))发起整理,一共统计了来自250个不同的人手写数字图片,其中50%是高中生,50%来自人口普查局的工作人员。该数据集的收集目的是希望通过算法,实现对手写数字的识别。其中本次使用的是从和鲸社区下载的一个数据集,包含已经进行分类的60000个训练集样本,以及10000个测试集样本。每个图片为一个 28 × 28 28\times28 28×28的图片矩阵。Kaggle上有一个基础项目就是mnist手写数据集识别,可以在上面进行测试。
在Heywhale.com数据集链接如下:
和鲸社区手写数字识别minst数据集链接
数据集样例(转成TXT形式)
1
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 124 253 255 63 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 96 244 251 253 62 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 127 251 251 253 62 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 68 236 251 211 31 8 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 60 228 251 251 94 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 155 253 253 189 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 20 253 251 235 66 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 32 205 253 251 126 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 104 251 253 184 15 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 80 240 251 193 23 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 32 253 253 253 159 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 151 251 251 251 39 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 48 221 251 251 172 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 234 251 251 196 12 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 253 251 251 89 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 159 255 253 253 31 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 48 228 253 247 140 8 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 64 251 253 220 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 64 251 253 220 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 24 193 253 220 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
3
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 42 118 219 166 118 118 6 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 103 242 254 254 254 254 254 66 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 18 232 254 254 254 254 254 238 70 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 104 244 254 224 254 254 254 141 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 207 254 210 254 254 254 34 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 84 206 254 254 254 254 41 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 24 209 254 254 254 171 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 91 137 253 254 254 254 112 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 40 214 250 254 254 254 254 254 34 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 81 247 254 254 254 254 254 254 146 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 110 246 254 254 254 254 254 171 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 73 89 89 93 240 254 171 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 128 254 219 31 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 7 254 254 214 28 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 138 254 254 116 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 19 177 90 0 0 0 0 0 25 240 254 254 34 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 164 254 215 63 36 0 51 89 206 254 254 139 8 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 57 197 254 254 222 180 241 254 254 253 213 11 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 140 105 254 254 254 254 254 254 236 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 7 117 117 165 254 254 239 50 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
5
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 31 40 129 234 234 159 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 68 150 239 254 253 253 253 215 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 156 201 254 254 254 241 150 98 8 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 19 154 254 236 203 83 39 30 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 144 253 145 12 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 10 129 222 78 79 8 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 134 253 167 8 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 255 254 78 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 201 253 226 69 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 55 6 0 18 128 253 241 41 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 25 205 235 92 0 0 20 253 253 58 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 231 245 108 0 0 0 132 253 185 14 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 121 245 254 254 254 217 254 223 50 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 116 165 233 233 234 180 39 3 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
关于实验设备,仅仅使用PC进行,故仅仅做了一些小的实验,部分算法由于时间复杂度太高,数据集都无法跑完。准确性的计算,根据数据集的特点仅仅使用训练集训练,测试集测试的简单形式(这种方式本身十分不合理,测试集应该一直处于黑箱状态的,但是这里仅仅是一种测试,所有没有考虑)。
关于训练目的,仅作为初学者对于一些基本机器学习算法进行实现,拒绝使用trick增加实践效果,并且仅仅使用有限的计算资源达到一个较好的训练效果。重在细节呈现以及对于多种测试模型进行一个简单的比对分析。
监督学习
ANN全连接神经网络的实现
第一个算法我尝试使用全连接神经网络进行实现,由于这是再2021年5月左右进行的,所以只能使用C++进行实现。而C++无法处理minst数据集那种文件格式(大概率只是我不会而已),所以使用python将minst手写数据集改写为TXT文档进行实现。
1.总述
此处使用的sigmoid型随机梯度下降法全连接神经网络进行实现(此处梯度下降、sigmoid函数讲解略去)。神经网络本质上使用了一个黑箱,近似在理论上可以近似模拟任何形式的函数。关于这一点,一种解释是从傅里叶变换出发,我目前没有非常搞懂,另一种是从三中普通类型的函数:带有逻辑运算的函数、分段函数和普通函数,这种更适合初学者理解。可以将每一种输入视为一个高维的点,而我们的算法则需要以一种特定的分类方式将这些数据进行分类。而根据今年的研究成果,使用隐藏层层数较多的神经网络模型对于这种黑箱函数的拟合效果非常优秀。全连接神经网络本质上应该是效果最好的一种NN模型,然而由于其包含过多的参数,所需要的巨大时间学习成本,并且在图像处理方面将每一个像素点一视同仁,实际上失去了各个像素点之间的连接特征,所以在实际操作中无法替代其他形式的神经网络。
这里神经网络分为三个部分:输入层、隐藏层和输出层。在手写数字识别时,输入层可以设置为 28 × 28 28\times28 28×28个特征(利用图像转化为一个 1 × ( 28 × 28 ) 1\times(28\times28) 1×(28×28)的输入矩阵),每个特征为图像的一个像素点。隐藏层每一层的个数以及设计的层数可以在后续进行参数调整。在输出层的每一个输入神经元与全连接层第一层的每一个神经元都进行连接。并且全连接层每一层的每一个神经元,都与下一层的每一个神经元进行连接。最终全连接层最后一层神经元与输出层连接。输出层这里设置为10个神经元,表示数字0~9。最终在这里使用一个max函数,取这10个神经元得到最大值的那一个神经元作为结果。
2.初始化
由于这里使用了sigmoid函数,所以需要规范化每一个神经元的数值。在输入层处将每一个输入参数除以350左右,使得每一个输入数值属于(0,1)区间。对于连接权值和偏置初始值的设定,大致也在 1 0 2 10^2 102的数量级左右,便于后续收敛。初始值不可以设置为0,否则后续可能出现“镜像”连接的情况,即每个连接权值、偏置都相同。
3.传播及损失
神经元传播公式如下: l a y e r n , t = s i g m o i d ( ∑ i = 1 n u m l a y e r n − 1 , i × w n − 1 , i , t + b i a s n , t ) layer_{n,t}=sigmoid(\sum_{i=1}^{num}layer_{n-1,i}\times w_{n-1,i,t}+bias_{n,t}) layern,t=sigmoid(i=1∑numlayern−1,i×wn−1,i,t+biasn,t) 对于每一个图像的输入函数,以及已有的神经网络,根据它的标签,可以将输出函数设计为如下形式: l a b e l = ( 0 , 0 , ⋯ 1 , ⋯ 0 , 0 ) label=(0,0,\cdots1,\cdots0,0) label=(0,0,⋯1,⋯0,0) 仅仅将其标签项设置为1,其余置0。根据神经网络计算出的输出层,可以构造输出向量 l a y e r 3 layer_{3} layer3,则损失loss可以设计为: l o s s = ∥ l a b e l − l a y e r 3 ∥ 2 loss=\Vert label-layer_{3} \Vert_{2} loss=∥label−layer3∥2 即两个向量作差的二范数形式。而神经网络的作用即是将神经网络训练得对于每一个训练集样本的损失最小。这个loss function也可以用其他方式设计,比如使用l-1范数或者其他范数形式。
4.反向传播
想做到使得loss更小,需要运用偏导的方法,即使用loss对于每一个神经元的偏置或者连接权值进行求导,再结合梯度下降的方式对新求得的偏置与权值进行计算。根据链式法则,根据输入到输出的形式,每一层顺序计算,求导的时候需要从较后的层数向较前的参数进行反向计算。这种形式即为反向传播: ∂ l o s s ∂ w n − 1 , i , t = ∂ l o s s ∂ l a y e r n , t × ∂ l a y e r n , t ∂ w n − 1 , i , t \frac{ \partial loss}{\partial w_{n-1,i,t}}=\frac{\partial loss}{\partial layer_{n,t}} \times \frac{ \partial layer_{n,t}}{\partial w_{n-1,i,t}} ∂wn−1,i,t∂loss=∂layern,t∂loss×∂wn−1,i,t∂layern,t
∂ l o s s ∂ b i a s n , t = ∂ l o s s ∂ l a y e r n , t × ∂ l a y e r n , t ∂ b i a s n , t \frac{ \partial loss}{\partial bias_{n,t}}=\frac{\partial loss}{\partial layer_{n,t}} \times \frac{ \partial layer_{n,t}}{\partial bias_{n,t}} ∂biasn,t∂loss=∂layern,t∂loss×∂biasn,t∂layern,t 这种形式进行传播,可以得到损失函数对于每一个权值以及偏置的偏导。再次使用梯度下降法: w n , i , t = w n , i , t − s t e p × ∂ l o s s w n , i , t w_{n,i,t}=w_{n,i,t}-step\times\frac{ \partial loss}{w_{n,i,t}} wn,i,t=wn,i,t−step×wn,i,t∂loss b i a s n , t = b i a s n , t − s t e p × ∂ l o s s b i a s n , t bias_{n,t}=bias_{n,t}-step\times\frac{\partial loss}{bias_{n,t}} biasn,t=biasn,t−step×biasn,t∂loss 这样就可以得到神经网络对于一次模型的学习结果。设置学习轮数,以及设置学习步长等参数,在每一轮学习过程中对每一个个体进行学习,最终可以得到较好的一组权值、偏置参数,使得对于每一个个体,得到尽可能小的损失值。
C++代码如下:
#include 最终获得的模型,在联想think book4核轻薄本上进行运行,调整2层全连接层,仅仅学习3000代的情况下,对于测试集可以达到91%的正确率。在vs code平台运行时间接近20分钟,在有限计算资源的情况下,效果是非常显著的。
对于全连接神经网络,可以发现,它将每一个像素点进行了完全的连接,这种连接方式失去了对于一些特征位置关系的判断。后续卷积神经网络卷积核的引入可以引入位置特征,但是将会失去全连接神经网络的精度。
决策树以及随机森林的实现
1.总述
单棵决策树已经被时代淘汰,然而随机森林却依然在机器学习领域拥有极高的地位,并且有着极大的实践意义。决策树或随机森林的时间空间复杂度确实太高,并且很难通过参数的调控使得复杂度降低。对于单棵决策树或者随机森林中的单棵决策树常常使用限制决策树层数的方式来进行复杂度的降低,以及过拟合的消除。但是考虑到个人的有限计算资源,对于60000个样本,每个样本拥有784个特征,如果控制决策树层数至可接受的范围,可预计最终呈现的效果十分糟糕;若使用随机森林建立完整的N课决策树,那么时间空间复杂度完全无法接受。故此处使用类似于卷积神经网络卷积核类似的方式或者PCA主成分分析法对每一个图片样本进行降维。此处使用了类似于卷积核的方式对图像样本进行降维处理。即将相邻的像素块用一定的方式表示为同一个特征元素。最终将 28 × 28 28\times28 28×28的特征降低为 10 × 10 10\times10 10×10进行处理。
2.单棵决策树的实现
注:这里采用的是最基本的未加入任何优化的ID3决策树模型。单棵决策树的实现,本质上是一个递归的过程。将所有的样本,按照二叉树的形式进行迭代分类直至叶子节点(如果进行剪枝规定了决策树最大深度,可能最终没有到达严格的叶子节点)。根节点包含了所有的测试集样本;而在这个巨大二叉树上的每一个节点,如果这个节点包含的样本标签统一,即说明这个节点已经成为了叶子节点;如果这个节点上样本标签并不统一,则需要进行一次二分,将这些样本分别分配到左右子节点上去。
分配的规则则一般有两种形式确定:信息熵与基尼系数。由于宿舍五楼挂了一张冯.诺依曼的照片,朝夕相处,他发明的信息熵对于我来说更加亲切,这里就使用信息熵作为进行分类的标准。
对于信息熵(infromation entropy)的理解,可以理解为一个信息以一种特定形式编码所需要占用的信编码量。通俗的解释,对于一个事件可能引申出的不同情况,存在 ∑ i = 1 n p i = 1 \sum_{i=1}^{n}p_{i}=1 ∑i=1npi=1的关系,不同情况发生的概率可能不同。对于一个确定概率的事件,对于某个传达了它确定发生的信息,它传达的信息量则可以根据它的概率进行大致的估计。这个事件原本发生的概率低,则其发生这个信息的信息量较大;其原本发生的概率高,则其发生这个信息的信息量较低。将信息熵使用en函数进行估计,则可以将一个事件所有情况的期望信息熵写作: e n t r o p y = ∑ i = 1 n p i × e n ( 1 p i ) entropy=\sum_{i=1}^{n}p_i\times en(\frac{1}{p_{i}}) entropy=i=1∑npi×en(pi1) 而若规定二进制编码表达信息,则公式引申为: e n t r o = − ∑ i = 1 n p i × log 2 p i entro=-\sum_{i=1}^{n}pi\times\log_{2}p_i entro=−i=1∑npi×log2pi个人感觉这个视频比较通俗易懂。信息熵基本原理视频链接
可以发现,这个信息熵的概率,实际上表达了一个事件的“混乱程度”。对于不同结果概率分布越均匀的事件,它的信息熵越低,反之越高。而回到决策树分类标准的部分,对于一个节点,每次只选取一种特征将他分为两类,而如果选取信息熵最大的特征则对于分类是最有效的,代表着这个特征最能区分两个类别的“特殊性”。
首先考虑基础情况:在某个节点只有两类样本,0和1,对于某个特征根据某个界限分类后,有 p 1 p_1 p1个样本的这种特征小于界限,而 p 2 p_2 p2样本的这种特征大于界限。那么对于这个特征以及这个界限进行分类,可以计算得到信息熵增益。
以这种形式对每一种特征以及每一个可能的分界点进行遍历,可以得到哪一种特征在哪一个位置进行划分是最适合进行分类的。对于可能的分界点,则采取对于所有样本进行排序并且哈希到 [ 0 , n ] [0,n] [0,n]的区间,可以使用0.5,1.5,2.5等中间值进行分界点的遍历。
其次考虑复杂情况,即这种多标签类型。在手写数字识别中存在0到9一共十种标签,而同样采取多标签归一为二分类问题:每一次再多加一层遍历,将每一个标签单独提出,再将其余八种标签视作一种标签。按照上面的方法,得到根据某一个标签和其余所有标签、某一种特征的某一个临界值进行二分类。
不考虑剪枝,对于有n个样本、m种特征,决策树的空间复杂度为 O ( n log n ) O(n\log n) O(nlogn),时间复杂度则为 O ( n log n × m n ( n log n ) ) O(n\log n \times mn(n\log n)) O(nlogn×mn(nlogn))这样的时间复杂度就十分的惊人了。在具体实现的过程中则需要尽可能减小n与m。在实际手写数字识别的操作中,尝试使用尽量少的样本,并且将图像进行了模糊处理,及采用取均值形式将图片转化为 10 × 10 10\times 10 10×10的矩阵(后面学习了CNN才知道这是一种池化方式,虽然比较容易想到,但是这里自己悟出来了还是很兴奋),即仅仅保留100个特征。而考虑剪枝,则大致可以控制最深的层数,到达最深的控制层数,若节点仍不为叶子,则取其中包含最多的那种样本作为叶子节点的分类。这个参数的调整事关过拟合或精度不够,需反复测试。在代码中前端的define部分可以自行调整参数。
原图示例:
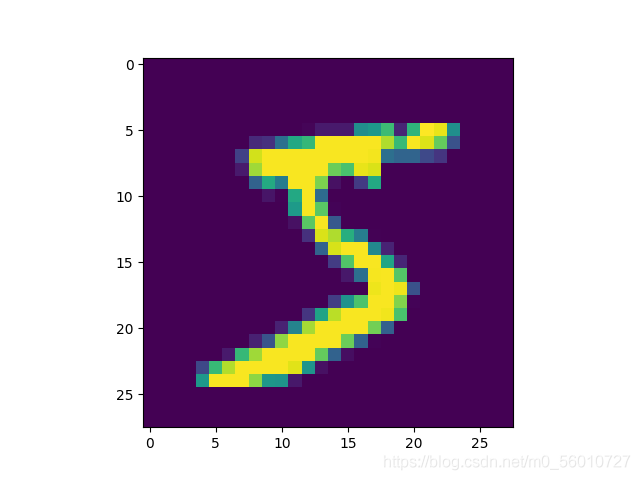
模糊化图像示例(模糊化为 10 × 10 10\times 10 10×10矩阵):

决策树虽然思路简单,但是实现难度较大。C++,ID3代码如下:
#include 限于设备,将图像模糊化到 16 × 16 16\times16 16×16,并且仅仅学习5000个样本,达到了34%的正确率。然而我尝试学习10000个样本的时候,从傍晚6点跑到晚上10点都没跑出来,所以就没有进行尝试了。如果使用60000个样本或许有着更高的准确率,然而确实证明ID3算法的时间复杂度实在太高了。如果为了更好的节约空间,上述的代码实现其实有很大的缺陷,如果动态建树可以节约大量的空间。上述仅仅是一个比较简单的模拟。
3.随机森林的实现
本质上即多棵决策树同时建立,但是每一棵决策树都使用了不同的建树规则,即随机建树。在每一棵树建立的过程中,大致流程与普通决策树相同,然而在每一个节点选择相应分类特征时,使用了随机挑选部分特恒的建树模式。由于这一随机性,导致每一棵决策树的结构并不相同,并且最终得到对于同一个样本的预测结果也不相同。然而使用较多的决策树,组成随机森林,最终使用投票的方式来决定某一个图像对于所有的树分类最多的那一种,降低过拟合,并且也增大了单棵决策树由于特征选取不合理导致误差较大的情况。
C++代码如下,ID3决策树组成决策森林:
#include 决策森林的效果明显比单棵决策树好太多了,当数图像降低到256个特征时,仅仅使用了10棵ID3决策树进行了1000个数据,1分钟内出结果,得到准确率已经超过决策树仅仅只有36%(500个样本多次测试,能达到大约24%到28%区间的正确率,由于随机性每次不同)。发现决策树时间复杂度的主要降低点可以借鉴随机森林的随机选择部分特征。如果每一层仅仅使用十分之一的特征,每一层都会降低一个数量级,最终算法复杂度大大降低,并且对最终的准确率影响不大。仍然限于设备问题,进一步的增大学习样本的测试并没有做,随机森林的复杂度仍然在一个较高的层次。
但是稍稍调整参数,调整参数为:学习3000个样本,决策树深度调整到14,图像降维到100个特征,建立30棵树,准确率竟然高达82%!无意中发现对图像进行降维处理,识别成功率反而增加了很多,并且仅仅使用单棵决策树也能达到63%。根据分析,猜测可能是由于我限于空间复杂度的考虑,将树的深度限制在15以内,当特征较多的时候,大多数情况并没有到达纯叶子节点。而将图像维度降低,反而准确率提升了很多。如此可以发现调节参数的一些特性。
用sklearn,Python跑的比CPP还快几十倍(应该是我手搓代码设计的问题)就不用降低维度了,直接784个维度直接跑60000个学习样本。速度快而且准确率还有96%
from sklearn.ensemble import RandomForestClassifier
import numpy as np
feature_num = 784 # 总特征数
learning_num = 60000 # 学习样本数
testing_num = 1000 # 测试样本数
N = 60000 # 总样本数
data = np.load("mnist.npz")
x_train = np.array(data['x_train']) # 学习集集图像
y_train = np.array(data['y_train']).flatten() # 学习集标签
x_test = np.array(data['x_test']) # 测试集图像
y_test = np.array(data['y_test']).flatten() # 测试集标签
X_train = []
for sample in x_train:
X_train.append(sample.flatten())
X_test = []
for sample in x_test:
X_test.append(sample.flatten())
rf = RandomForestClassifier(n_estimators=20, criterion="entropy", max_depth=20)
rf.fit(X_train, y_train)
print(rf.score(X_test, y_test))
PCA(SVD)主成分分析+自适应距离度量+KNN近邻算法的实现
1.总述
斯坦福cs231n课程明确提出:KNN以及K-means不适合于对于图像进行处理。(原话是"never used")但是从kaggle上看对于mnist数据集某些范数形式效果还是很不错的。
对于KNN一级下文中使用的K-means聚类方法,在实际操作的过程中,发现这两种算法的理解以及代码实现属于最简单的类型,但是直接使用l-p范数对图像距离进行度量,效果极差。可以得出实际KNN以及K-means这类算法的关键在于距离度量的形式。有了好的距离度量方式,才可以谈及后续的项目实现。后面K-means部分,作者提到在实现K-means的时候简单使用了l-2范数来进行手写数字样本的距离测算,最终发现同一种数字样本仅仅因为位置移动、大小不同或者写法风格不同,距离差异反而极其巨大。
在KNN以及K-means的研究中,作者首先尝试仅仅从距离度量方式入手,使用了一些极其复杂的方法进行实验,但是效果均不是非常理想。所以这里先尝试使用PCA对数据进行降噪处理,然后再进行KNN或者K-means的实现。
2.PCA主成分分析
此处一般使用PCA主成分分析方法,对样本进行主成分的分解,并且尽量投影到2D或者3D图上可视化,观察样本是否可分。关于PCA有两种方式,一种是基于特征值分解,另外一种是基于奇异值分解,不过实际上大同小异(sklearn携带的PCA标准库使用的SVD方法)。
PCA一个形象的入门讲解
Stanford CS231 CV基础 KNN
PCA的本质,实际上通过上面的视频可以得出,将样本集进行减去均值的处理得到X矩阵,再得到协方差矩阵 X X T XX^T XXT后,进行特征值分解(或者奇异值分解),得到的特征向量对应的这个特征值,即是样本在这个方向的方差。而样本在这个方向上的方差越大,也意味着所有样本到达这个方向轴的距离平方和最小。意味着某个特征值越大,其对应的特征向量所代表的的方向作为基向量,进行表示的效果越好。最终可以取新的基向量空间表示所有的样本,并且可以仅仅保留前K组向量,可以达到降噪、便于计算储存以及可视化的作用。
Python3代码如下,PCA降维并可视化
import numpy as np
from random import *
import matplotlib.pyplot as plt
feature_num=784 # 总特征数
learning_num = 3000 # 学习样本数
N = 60000 # 总样本数
data = np.load("mnist.npz")
label = [0 for i in range(N)]
x_train = data['x_train'] # 学习集集图像
y_train = data['y_train'] # 学习集标签
x_test = data['x_test'] # 测试集图像
y_test = data['y_test'] # 测试集标签
X=np.zeros((feature_num,learning_num))
for i in range(learning_num): # 遍历样本
for j in range(feature_num): # 遍历特征
X[j][i]=x_train[i][j//28][j%28]
mean = np.array([np.mean(X[:,i]) for i in range(learning_num)])
X=X-mean
T=np.dot(X,X.T)
aa,values,vectors=np.linalg.svd(T)
eig_pairs = [(np.abs(values[i]), vectors[:, i]) for i in range(feature_num)] # 将特征值和特征向量提出
eig_pairs.sort(key=lambda tup: tup[0],reverse=True) # 对特征值进行排序
x_axis=np.dot(X.T,eig_pairs[0][1]) # 取p1
y_axis=np.dot(X.T,eig_pairs[1][1]) # 取p2
for i in range(learning_num):
if y_train[i]==0:
plt.scatter(x_axis[i],y_axis[i],s=15,color="red")
if y_train[i]==1:
plt.scatter(x_axis[i],y_axis[i],s=15,color="orange")
if y_train[i]==2:
plt.scatter(x_axis[i],y_axis[i],s=15,color="purple")
if y_train[i]==3:
plt.scatter(x_axis[i],y_axis[i],s=15,color="blue")
if y_train[i]==4:
plt.scatter(x_axis[i],y_axis[i],s=15,color="green")
if y_train[i]==5:
plt.scatter(x_axis[i],y_axis[i],s=15,color="grey")
if y_train[i]==6:
plt.scatter(x_axis[i],y_axis[i],s=15,color="black")
if y_train[i]==7:
plt.scatter(x_axis[i],y_axis[i],s=15,color="brown")
if y_train[i]==8:
plt.scatter(x_axis[i],y_axis[i],s=15,color="deeppink")
if y_train[i]==9:
plt.scatter(x_axis[i],y_axis[i],s=15,color="darkred")
plt.show()
以下是使用PCA分解到2维平面对mnist数据集1000个样本的降维效果。
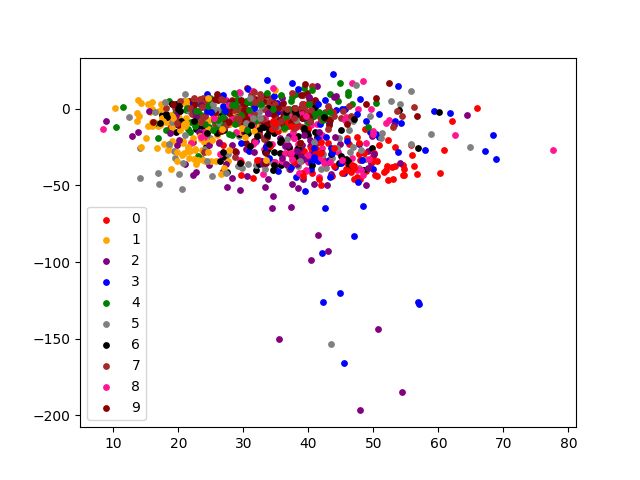
对于前15个奇异值的碎石图:

可以看到,从第十个奇异值开始,对于总体方差的贡献就比较小了。主成分大约保留K=100左右预计效果比较好。并且有较好的降噪效果。
3.KNN近邻算法
KNN几乎是计算开销最小的一种分类器算法。主要思路也较为简单,在拥有含有标签的数据集的情况下,确定K值,对于测试数据进行与每个学习样本的距离测算。找出最近的K个(对于不同标签的样本数量不同,可能考虑在这个距离基础上进行一些操作)最终将这个测试样本划分到被选中样本计算值最大的一类。这种简单算法的关键在于K值的确定以及距离的度量方式。
4.自适应距离度量
经过PCA主成分分解之后,先尝试大致取前k个主成分。尝试进行KNN的计算。在K-means实现过程中已经了解到,直接使用范数对于图像距离度量效果较差。此时需要学习距离度量方式。
CNN卷积神经网络的实现
1.总论
卷积神经网络早在上个世纪即被提出,然而直到21世纪10年代才成为学术界主流研究方向,这种模型被证明对于图像处理有着极其优秀的效果。正如上文ANN提到,ANN全连接对于计算造成了巨大的损耗,比如手写数字识别是784个特征,第一层使用20个神经元,则需要 784 × 20 784\times 20 784×20次连接。如果是RGB格式的图像,并且每一层有更高的位数,仅仅第一层的参数可能就会达到 1 0 4 10^4 104级别,后面每层神经元如果数量设置更多的话,可能造成参数过多计算量过大的问题。
可以得出,生物视觉在识别一个图像时,实际上并没有把整个图像的每一个细节都进行观测,而是进行主要特征的提取。
斯坦福的一个CS231n的演示网站:CNN演示网站
2.卷积层
个人认为,卷积提取特征是一种较为“玄学”的方法。在Pytorch等框架下,卷积核甚至在某些设置下是随机生成的。每一次卷积运算,可以提取图像的某一种特征。卷积的模式是使用滑动窗口,将特定的卷积核进行扫描并且按元素位置相乘,最终求元素和,将得到的值放入新的图像位(需要加入偏置调节像素点值)。
关于几种常用卷积核的测试结果:
原图:
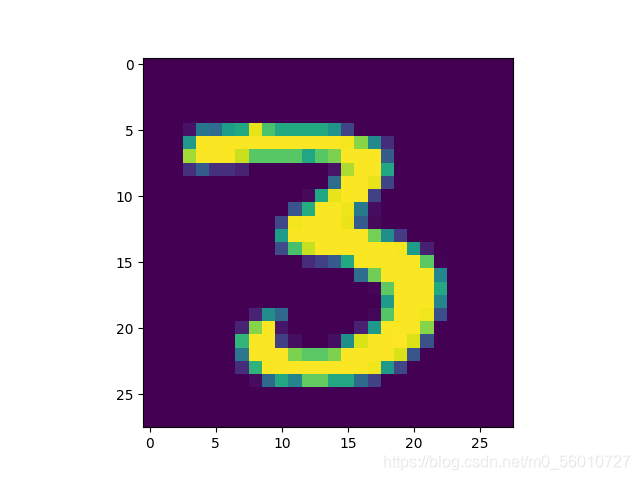
均值卷积核: [ 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9 1 9 ] \left[ \begin{matrix} \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \\ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{matrix} \right] ⎣⎡919191919191919191⎦⎤

锐化卷积核(加强边界特征): [ − 1 − 1 − 1 − 1 9 − 1 − 1 − 1 − 1 ] × 1 16 \left[ \begin{matrix} -1 & -1 &-1 \\-1 &9 & -1 \\ -1 & -1 & -1 \end{matrix} \right] \times \frac{1}{16} ⎣⎡−1−1−1−19−1−1−1−1⎦⎤×161
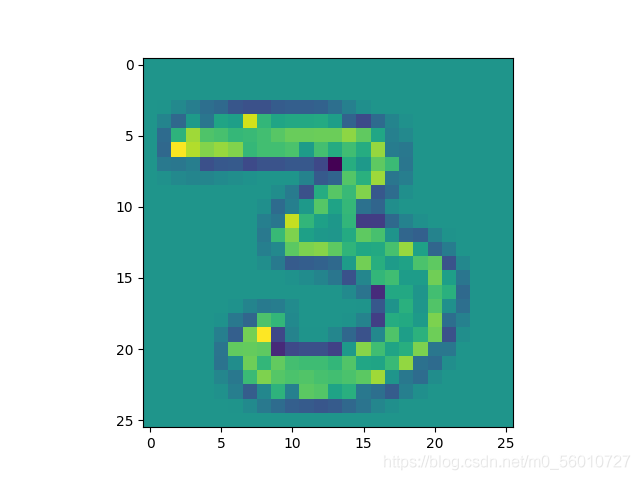
Laplace算子卷积核(提取边缘特征): [ 0 1 0 1 − 4 1 0 1 0 ] \left[ \begin{matrix} 0 & 1 &0 \\1 &-4 &1 \\ 0 & 1 & 0 \end{matrix} \right] ⎣⎡0101−41010⎦⎤

水平卷积核(水平边缘检测):
[ 1 1 1 0 0 0 − 1 − 1 − 1 ] \left[ \begin{matrix} 1 & 1 &1 \\0 &0 &0\\ -1 & -1 & -1 \end{matrix} \right] ⎣⎡10−110−110−1⎦⎤
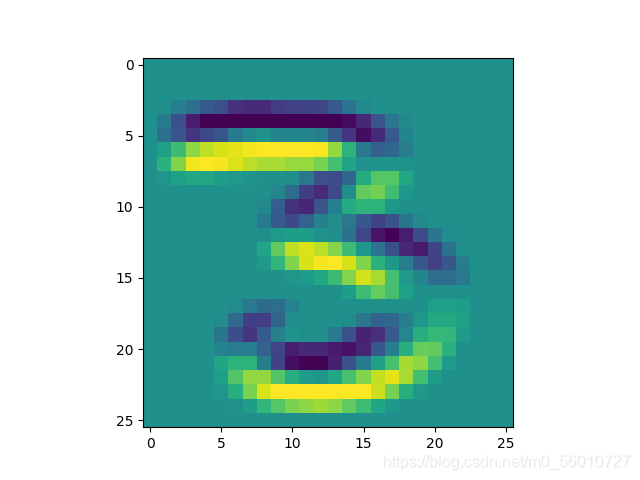
可以看出,使用不同的卷积核(滤波器),得到的图像特征是不同的。对于不同的图像,使用卷积化可以减少特征的同时减少参数的使用。
3.激励层
此处使用RELU激活函数。 R E L U ( x ) = m a x ( 0 , α x ) RELU(x)=max(0,\alpha x) RELU(x)=max(0,αx)

保留0以上特征,消除负特征。
4.池化层
池化大致分为三种类型:均值池化,最大值池化和随机池化。
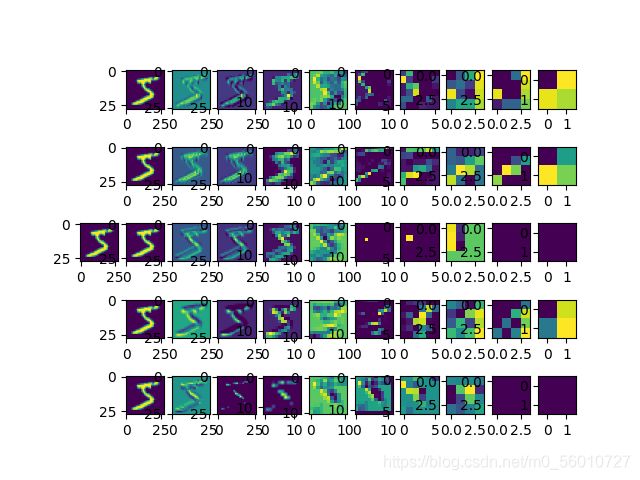
CNN卷积部分效果图:取5个特征通道,使用con+relu+pool形式,一共三次组合。
5.全连接层(接ANN或者DNN)
全连接层直接可以接ANN或DNN模板。此时经过前期的预处理,图像的特征已经大致保留并且减少。这种情况下,可以大大减少使用全连接神经网络的计算量。这一点在手写数字识别体现的并不明显,因为特征本来就少,使用CNN确实是杀鸡用牛刀。
6.反向传播
CNN的反向传播需要一些特殊的处理,对于池化层(max和average两种情况需要分别作不同的处理)。
1.反池化
(1)max池化反池化: p o o l i n g : [ 1 2 3 4 ] t o [ 4 ] pooling:\left[ \begin{matrix} 1 & 2 \\3 & 4 \end{matrix} \right]to\left[\begin {matrix}4\end {matrix}\right] pooling:[1324]to[4] a n t i p o o l i n g : [ 4 ] t o [ 0 0 0 4 ] antipooling:[4]to\left[\begin{matrix}0&0\\0&4\end{matrix}\right] antipooling:[4]to[0004]
(2)均值池化反池化: p o o l i n g : [ 1 2 3 4 ] t o [ 2.5 ] pooling:\left[ \begin{matrix} 1 & 2 \\3 & 4 \end{matrix} \right]to\left[\begin {matrix}2.5\end {matrix}\right] pooling:[1324]to[2.5] a n t i p o o l i n g : [ 2.5 ] t o [ 2.5 2.5 2.5 2.5 ] antipooling:[2.5]to\left[\begin{matrix}2.5&2.5\\2.5&2.5\end{matrix}\right] antipooling:[2.5]to[2.52.52.52.5]
后续根据反池化得到的矩阵进行反向传播即可。
2.反卷积
Python代码如下:
my_layers.py
import numpy as np
def affine_forward(x, w, b): # (batch_size,n1) (n1,n2) (n2)
out = np.dot(x, w) + b # (batch_size,n2)
cache = (x, w, b)
return out, cache
def affine_backward(dout, cache): # (batch_size,n2)
x, w, b = cache
dx, dw, db = np.dot(dout, w.T), np.dot(x.T, dout), np.sum(dout, axis=0)
return dx, dw, db
def relu_forward(x): # (batch_size,n)
cache = x
out = x
out[x < 0] = 0
return out, cache
def relu_backward(dout, cache):
dcache = dout
dcache[cache <= 0] = 0
return dcache
def softmax_loss(x, y): # y: (batch_size) the label
loss = 0
p = np.exp(x)
p /= np.sum(p)
dx = p
for i in range(x.shape[0]):
loss += -np.log(p[i][y[i]])
dx[i][y[i]] = p[i][y[i]] - 1
return loss, dx
def dropout_forward(x, dropout_param):
if dropout_param['mode'] == 'test' or dropout_param['p'] == 1:
return x, dropout_param
mask = np.ones(np.shape(x))
p, mode = dropout_param['p'], dropout_param['mode']
if 'seed' in dropout_param:
np.random.seed(dropout_param['seed'])
mask = np.random.random(np.shape(x)) / p
mask.where(mask < 1, 0, 1)
out = x * mask
cache = (mask, dropout_param)
return out, cache
def dropout_backward(dout, cache):
mask, dropout_param = cache
dx = dout
if dropout_param['mode'] == 'train':
dx = dout * mask
return dx
def batchnorm_forward(x, gamma, beta, bn_param):
mode = bn_param['mode']
eps = bn_param.get('eps', 1e-5)
momentum = bn_param.get('momentum', 0.9)
N, D = x.shape
running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))
out, cache = None, None
if mode == 'train':
sample_mean = np.mean(x, axis=0, keepdims=True) # [1,D]
sample_var = np.var(x, axis=0, keepdims=True) # [1,D]
x_normalized = (x - sample_mean) / np.sqrt(sample_var + eps) # [N,D]
out = gamma * x_normalized + beta
cache = (x_normalized, gamma, beta, sample_mean, sample_var, x, eps)
running_mean = momentum * running_mean + (1 - momentum) * sample_mean
running_var = momentum * running_var + (1 - momentum) * sample_var
elif mode == 'test':
x_normalized = (x - running_mean) / np.sqrt(running_var + eps)
out = gamma * x_normalized + beta
else:
raise ValueError('Invalid forward batchnorm mode "%s"' % mode)
bn_param['running_mean'] = running_mean
bn_param['running_var'] = running_var
return out, cache
def batchnorm_backward(dout, cache):
x_normalized, gamma, beta, sample_mean, sample_var, x, eps = cache
N, D = x.shape
dx_normalized = dout * gamma # [N,D]
x_mu = x - sample_mean # [N,D]
sample_std_inv = 1.0 / np.sqrt(sample_var + eps) # [1,D]
dsample_var = -0.5 * np.sum(dx_normalized * x_mu, axis=0, keepdims=True) * sample_std_inv ** 3
dsample_mean = -1.0 * np.sum(dx_normalized * sample_std_inv, axis=0, keepdims=True) - \
2.0 * dsample_var * np.mean(x_mu, axis=0, keepdims=True)
dx1 = dx_normalized * sample_std_inv
dx2 = 2.0 / N * dsample_var * x_mu
dx = dx1 + dx2 + 1.0 / N * dsample_mean
dgamma = np.sum(dout * x_normalized, axis=0, keepdims=True)
dbeta = np.sum(dout, axis=0, keepdims=True)
return dx, dgamma, dbeta
def conv_forward_naive(x, w, b, conv_param): # b:(F)
stride, pad = conv_param['stride'], conv_param['pad']
N, C, H, W = np.shape(x) # pictures
F, C, HH, WW = np.shape(w) # filters
h = 1 + (H + 2 * pad - HH) / stride
w = 1 + (W + 2 * pad - WW) / stride
new_x = np.pad(x, (pad), "constant", constant_values=(0))
out = np.zeros((N, F, h, w))
for i in range(N):
for f in range(F):
for j in range(h):
for k in range(w):
out[i, f, j, k] = np.sum(
new_x[i, :, j * stride:j * stride + HH, k * stride:k * stride + WW] * w[f, :, :, :] + b[f])
cache = (x, w, b, conv_param)
return out, cache # out:(N, F, h, w)
def conv_backward_naive(dout, cache): # dout:(N, F, h, w)
x, w, b, conv_param = cache
stride, pad = conv_param['stride'], conv_param['pad']
N, C, H, W = np.shape(x) # pictures
F, C, HH, WW = np.shape(w) # filters
h = 1 + (H + 2 * pad - HH) / stride
w = 1 + (W + 2 * pad - WW) / stride
new_x = np.pad(x, (pad), "constant", constant_values=(0))
dw = np.zeros_like(w)
db = np.zeros_like(b)
dx = np.zeros_like(new_x)
for i in range(N):
for f in range(F):
for j in range(h):
for k in range(w): # (j,k)->(j*stride:j*stride+HH, k*stride:k*stride+WW)
dx[i, :, j * stride:j * stride + HH, k * stride:k * stride + WW] += w[f] * dout[i, f, j, k]
db[f] += dout[i, f, j, k]
dw[f] += new_x[i, :, j * stride:j * stride + HH, k * stride:k * stride + WW] * dout[i, f, j, k]
dx = dx[:, :, pad:pad + H, pad:pad + W]
return dx, dw, db
def max_pool_forward_naive(x, pool_param): # tacit consent that it could be divided with no remainder
N, C, H, W = np.shape(x)
stride, HH, WW = pool_param['stride'], pool_param['pool_height'], pool_param['pool_width']
hh = 1 + (H - HH) / stride
ww = 1 + (W - WW) / stride
out = np.zeros((N, C, hh, ww))
for i in range(N):
for c in range(C):
for j in range(hh):
for k in range(ww):
out[i, c, j, k] = np.max(x[i, c, j * stride:j * stride * HH, k * stride:k * stride + WW])
cache = (x, pool_param)
for i in range(N):
for c in range(C):
for j in range(hh):
for k in range(ww):
out[i, c, j, k] = np.max(x[i, c, j * stride:j * stride + HH, k * stride:k * stride + WW])
return out, cache
def max_pool_backward_naive(dout, cache):
x, pool_param = cache
N, C, H, W = np.shape(x)
stride, HH, WW = pool_param['stride'], pool_param['pool_height'], pool_param['pool_width']
hh = 1 + (H - HH) / stride
ww = 1 + (W - WW) / stride
dx = np.zeros(np.shape(x))
for i in range(N):
for c in range(C):
for j in range(hh):
for k in range(ww):
max_val = np.max(x[i, c, j * stride:j * stride + HH, k * stride:k * stride + WW])
for l in range(j * stride, j * stride + HH):
for m in range(k * stride, k * stride + WW):
if x[i, c, l, m] == max_val:
dx[i, c, l, m] = dout[i, c, j, k]
return dx
CNN.py
from my_layers import *
import cv2
import matplotlib.pyplot as plt
# conv1-relu1-pool1-conv2-relu2-pool2-conv3-relu3-conv3-
# layer1-dropout1-relu1-layer2-dropout2-relu2-layer3-dropout3-relu3-softmax
def unpickle(file):
import pickle
with open(file, 'rb') as fo:
dict = pickle.load(fo, encoding='bytes')
return dict
def show_picture(x): # show a picture
image_m = np.reshape(x, (3, 32, 32))
r = image_m[0, :, :]
g = image_m[1, :, :]
b = image_m[2, :, :]
img23 = cv2.merge([r, g, b])
plt.figure()
plt.imshow(img23)
plt.show()
length = 3072
# 加载测试集
dict_data = []
dict_data.append(unpickle("data_batch_1"))
dict_data.append(unpickle("data_batch_2"))
dict_data.append(unpickle("data_batch_3"))
dict_data.append(unpickle("data_batch_4"))
dict_data.append(unpickle("data_batch_5"))
for i in range(5):
for j in range(len(dict_data[i][b'data'])):
dict_data[i][b'data'][j] = np.array(dict_data[i][b'data'][j]) # 3072
class FullyConnectedNet(object): # layer1-dropout1-relu1-layer2-dropout2-relu2-layer3-dropout3-relu3-softmax
def __init__(self, input_dim, num_classes=10, dropout_keep_ratio=1, normalization=None,
reg=0.0, weight_scale=1e-2, seed=None,
):
self.input_dim = input_dim
self.num_classes = num_classes
self.normalization = normalization
self.reg = reg
self.weight_scale = weight_scale
self.params = {
}
self.params['W1'] = weight_scale * np.random.random((self.input_dim, 30))
self.params['b1'] = np.zeros(30)
self.params['W2'] = weight_scale * np.random.random((30, 30))
self.params['b2'] = np.zeros(30)
self.params['W3'] = weight_scale * np.random.random((30, 10))
self.params['b3'] = np.zeros(10)
self.dropout_param = {
}
self.dropout_param['seed'] = seed
self.dropout_param['p'] = dropout_keep_ratio
def forward(self, X, mode='test', dropout_ratio=1):
self.dropout_param['mode'] = mode
self.dropout_param['p'] = dropout_ratio
self.input = X
self.layer1, self.cachelayer1 = affine_forward(self.input, self.params['W1'], self.params['b1'])
self.drop1, self.cachedrop1 = dropout_forward(self.layer1, self.dropout_param)
self.relu1, self.cacherelu1 = relu_forward(self.drop1)
self.relu2, self.cachelayer2 = affine_forward(self.relu1, self.params['W2'], self.params['b2'])
self.drop2, self.cachedrop2 = dropout_forward(self.relu2, self.dropout_param)
self.layer3, self.cachelayer3 = affine_forward(self.drop2, self.params['W3'], self.params['b3'])
self.drop3, self.cachedrop3 = dropout_forward(self.layer3, self.dropout_param)
self.relu3, self.cacherelu3 = relu_forward(self.drop3)
return np.argmax(self.relu3)
def backward(self, mode='test', learning_rate=0.01):
self.dropout_param['mode'] = mode
drelu3 = relu_backward(self.dout, self.cachelayer3)
ddrop3 = dropout_backward(drelu3, self.cachedrop3)
dlayer3 = affine_backward(ddrop3, self.cachelayer3)
self.params['W3'] -= learning_rate * dlayer3[1]
self.params['b3'] -= learning_rate * dlayer3[2]
drelu2 = relu_backward(dlayer3[0], self.cachelayer2)
ddrop2 = dropout_backward(drelu2, self.cachedrop2)
dlayer2 = affine_backward(ddrop2, self.cachelayer2)
self.params['W2'] -= learning_rate * dlayer2[1]
self.params['b2'] -= learning_rate * dlayer2[2]
drelu1 = relu_backward(dlayer2[0], self.cachelayer2)
ddrop1 = dropout_backward(drelu1, self.cachedrop1)
dlayer1 = affine_backward(ddrop1, self.cachelayer1)
self.params['W1'] -= learning_rate * dlayer1[1]
self.params['b1'] -= learning_rate * dlayer1[2]
def loss(self, X, y, mode='test'):
self.forward(X, mode)
loss, self.dout = softmax_loss(self.relu3, y)
return loss
class ConvNet(object): # conv1-relu1-pool1-conv2-relu2-pool2-conv3-relu3-conv3-FullConnectedLayer
def __init__(self, input_dim=(3, 32, 32), connect_conv=0, use_batchnorm=False,
weight_scale=1e-3, reg=0.0):
self.use_connect_conv = connect_conv > 0
self.use_batchnorm = use_batchnorm
self.input_dim = input_dim
self.reg = reg
self.W1 = weight_scale * np.random.random((10, self.input_dim[0], 3, 3))
self.b1 = np.zeros(10)
self.W2= weight_scale * np.random.random((10, self.input_dim[0], 3, 3))
self.b2 = np.zeros(10)
self.W3= weight_scale * np.random.random((10, self.input_dim[0], 3, 3))
self.b3 = np.zeros(10)
self.convparam = {
} # 'stride' 'pad'
self.convparam['stride'] = 1
self.convparam['pad'] = 1
self.poolparam = {
} # stride height width
def forward(self, X):
self.input = X # 3*32*32
self.conv1, self.cacheconv1 = conv_forward_naive(self.input, self.W1, self.b1, self.convparam) # 10*32*32
self.relu1, self.cacherelu1 = relu_forward(self.conv1) # 10*32*32
self.poolparam['stride']=16
self.poolparam['height']=16
self.poolparam['width']=16
self.pool1, self.cachepool1 = max_pool_forward_naive(self.relu1, self.poolparam) # 10*16*16
self.conv2, self.cacheconv2 = conv_forward_naive(self.input, self.W1, self.b1, self.convparam) # 10*16*16
self.relu2, self.cacherelu2 = relu_forward(self.conv1) # 10*16*16
self.poolparam['stride'] = 8
self.poolparam['height'] = 8
self.poolparam['width'] = 8
self.pool2, self.cachepool2 = max_pool_forward_naive(self.relu1, self.poolparam) # 10*8*8
self.conv3, self.cacheconv3 = conv_forward_naive(self.input, self.W1, self.b1, self.convparam) # 10*8*8
self.relu3, self.cacherelu3 = relu_forward(self.conv1) # 10*8*8
self.poolparam['stride'] = 4
self.poolparam['height'] = 4
self.poolparam['width'] = 4
self.pool3, self.cachepool3 = max_pool_forward_naive(self.relu1, self.poolparam) # 10*4*4
self.out = self.pool3.flatten() # 160
return self.out
def backward(self, dout, learning_rate = 0.01):
dout=dout.reshape((10,4,4))
dpool3= max_pool_backward_naive(dout, self.cachepool3)
drelu3= relu_backward(dpool3, self.cacherelu3)
dconv3= conv_backward_naive(drelu3, self.cacheconv3)
self.W3-=learning_rate * dconv3[1]
self.b3-=learning_rate * dconv3[2]
dpool2 = max_pool_backward_naive(dconv3, self.cachepool3)
drelu2 = relu_backward(dpool2, self.cacherelu3)
dconv2 = conv_backward_naive(drelu2, self.cacheconv3)
self.W2 -= learning_rate * dconv2[1]
self.b2 -= learning_rate * dconv2[2]
dpool1 = max_pool_backward_naive(dconv2, self.cachepool3)
drelu1 = relu_backward(dpool1, self.cacherelu3)
dconv1 = conv_backward_naive(drelu1, self.cacheconv3)
self.W1 -= learning_rate * dconv1[1]
self.b1 -= learning_rate * dconv1[2]
class NeuralNetwork():
def __init__(self):
self.cnn=ConvNet()
self.ann=FullyConnectedNet(160)
def forward(self, X):
ann_input= self.cnn.forward(X)
return self.ann.forward(ann_input)
def loss(self, X, y=None, mode='train'):
self.forward(X)
return self.ann.loss(X, y)
def backward(self):
dann = self.ann.backward()
self.cnn.backward(dann)
def train(self, X, y, iter_times=1000, batch_size=100):
num = X.shape[0]
for i in range(iter_times):
select = np.random.choice(num, batch_size, replace=False, detype='int')
x_batch = X[select]
y_batch = y[select].astype(np.int32)
self.loss(x_batch, y_batch)
self.backward()
def score(self, X, Y):
ans= self.forward(X)
num = X.shape[0]
return np.sum(ans==y)/num
nn = NeuralNetwork()
SVM支持向量机的实现
我实在是看不懂SVM背后的一些数学原理,手搓部分留到大二上半期的《最优化导论》课程上完了来吧……先用sklearn凑合写一写。参数调了一下,大致默认的高斯核函数效果比较好,惩罚项调成默认的1。
import numpy as np
import matplotlib.pyplot as plt
import sklearn.svm as svc
feature_num = 784 # 总特征数
learning_num = 60000 # 学习样本数
testing_num = 1000 # 测试样本数
N = 60000 # 总样本数
data = np.load("mnist.npz")
x_train = np.array(data['x_train']) # 学习集集图像
y_train = np.array(data['y_train']).flatten() # 学习集标签
x_test = np.array(data['x_test']) # 测试集图像
y_test = np.array(data['y_test']).flatten() # 测试集标签
X_train=[]
for sample in x_train:
X_train.append(sample.flatten())
X_test=[]
for sample in x_test:
X_test.append(sample.flatten())
svc1=svc.SVC(C=1, kernel="rbf")
svc1.fit(X_train,y_train)
print(svc1.score(X_test,y_test))
最后得到的准确率是97.2%……确实库比自己造的车轮好用……
朴素贝叶斯的实现
1.总论
朴素贝叶斯是一种非常简单且容易理解的机器学习算法,代码量也比较小,且在实际操作中效果也比较好。对于朴素贝叶斯基本仅仅基于简单的概率论方面的推导,可解释性较强。
对于mnist手写数字集,可以直接使用784个特征进行计算,也可以先进行PCA主成分分解或者简单的pooling操作。对于每一个图像,可以得到n个处理过的特征值组成的集合K,对于m个样本,则有集合 K i K_i Ki表示每一个样本。有 K i = { K i , 1 , K i , 2 , ⋯ , K i , n } K_i=\{K_{i,1},K_{i,2},\cdots ,K_{i,n}\} Ki={ Ki,1,Ki,2,⋯,Ki,n}。存在这样一个基本定理: P ( A ∣ C ) × P ( C ) = P ( C ∣ A ) × P ( A ) = P ( A , C ) P(A|C)\times P(C)=P(C|A)\times P(A)=P(A,C) P(A∣C)×P(C)=P(C∣A)×P(A)=P(A,C) 可以推出: P ( A ∣ C ) = P ( C ∣ A ) × P ( A ) P ( C ) P(A|C)=\frac{P(C|A)\times P(A)}{P(C)} P(A∣C)=P(C)P(C∣A)×P(A) 即后验概率可以由先验概率得出。而先验概率在通常意义下可以视为已知条件推出某个结果的概率,而后验概率则为已知某个结果已经发生,出现某些条件的概率。对于手写数字识别而言,本质上则是对于每一个学习样本,将这个图像所有特征视为某个条件,需要验证它对于 1 , 2 ⋯ 9 1,2\cdots9 1,2⋯9这几种分类结果谁拥有最大的可能性。则将集合 { 1 , 2 , 3 ⋯ 9 } \{1,2,3\cdots9\} { 1,2,3⋯9}记为T。则对于一个样本K_i,将其归类为D,则 D = arg max t P ( t ∣ K i ) = arg max t P ( K i ∣ t ) × P ( t ) P ( K i ) = arg max t ∏ r = 1 n P ( K i , r ∣ t ) × P ( t ) ∏ r = 1 n P ( K i , r ) D=\argmax_{t}{P(t|K_i)}=\argmax_{t}{\frac{P(K_i|t)\times P(t)}{P(K_i)}}=\argmax_{t}{\frac{\prod _{r=1}^{n}P(K_{i,r}|t)\times P(t)}{\prod _{r=1}^{n}P(K_{i,r})}} D=targmaxP(t∣Ki)=targmaxP(Ki)P(Ki∣t)×P(t)=targmax∏r=1nP(Ki,r)∏r=1nP(Ki,r∣t)×P(t) 所有的先验概率都是可以使用训练集求得的,将训练集得到的所有概率参数视为整体参数,则对于测试集的每一个样本得到D就比较简单了。
2.视作连续型数值预处理以及先验概率计算(效果较差)
对于每一个像素点,均为0-255的整数值。则此处对于数值应该有一个划分。需要预处理得到所有的 P ( K i , r ∣ t ) P(K_{i,r}|t) P(Ki,r∣t)以及 P ( t ) P(t) P(t)和 P ( K i , r ) P(K_{i,r}) P(Ki,r)。对于特定的测试样本 K i K_{i} Ki,考虑分子部分。使用训练集的概率来进行计算,则可以得到 P ( t ) = ∣ K t ∣ ∑ 0 9 ∣ K i ∣ P(t)=\frac{|K_t|}{\sum^{9}_{0}|K_i|} P(t)=∑09∣Ki∣∣Kt∣ 对于 P ( K i , r ∣ t ) P(K_{i,r}|t) P(Ki,r∣t),由于其属于连续性变量,使用概率密度函数对其进行分布,对于r特征,t类别, K i , r K_{i,r} Ki,r大小可能的概率为: P ( K i , r ∣ t ) = 1 2 π σ t , r × e − ( K i , r − μ t , r ) 2 2 σ 2 t , r P(K_{i,r}|t)=\frac{1}{\sqrt {2\pi}\sigma_{t,r}}\times e^{-\frac{(K_{i,r}-\mu_{t,r})^2}{2\sigma^2{t,r}}} P(Ki,r∣t)=2πσt,r1×e−2σ2t,r(Ki,r−μt,r)2 同理,分母部分同样使用正态分布进行估计。此时,对于t类别r特征,则需要提前预处理得出所有的概率因子。
使用正态分布估计先验概率的失败代码:
import numpy as np
feature_num=784 # 总特征数
learning_num = 1000 # 学习样本数
testing_num = 100 # 测试样本数
K = 10 # 总类别数
N = 60000 # 总样本数
pca_num = 3 # 压缩特征维度
data = np.load("mnist.npz")
x_train = data['x_train'] # 学习集集图像
y_train = data['y_train'] # 学习集标签
x_test = data['x_test'] # 测试集图像
y_test = data['y_test'] # 测试集标签
# 读入训练集与测试集样本
x=np.zeros((learning_num,feature_num)) # 学习样本
for i in range(learning_num):
for j in range(feature_num):
x[i][j]=x_train[i][j//28][j%28] # 样本向量化
y=np.zeros((testing_num,feature_num)) # 测试样本
for i in range(testing_num):
for j in range(feature_num):
y[i][j] = x_test[i][j // 28][j % 28] # 样本向量化
# 初始化先验概率
total=np.zeros((K,1)) # 每种标签数量
P_t=np.zeros((K,1)) # 10个类别的样本数目概率
aver=np.zeros((K,feature_num)) # 对于每种样本每个特征的平均值
sigma=np.zeros((K,feature_num)) # 对于每种样本每个特征的标准差
total_aver=np.zeros((feature_num,1)) # 对于所有样本每个特征的平均值
total_sigma=np.zeros((feature_num,1)) # 对于所有样本每个特征的标准差
for i in range(learning_num):
label=y_train[i]
total[label]+=1
for j in range(feature_num):
aver[label][j]+=x[i][j]
total_aver[j]+=x[i][j]
for j in range(feature_num): # 求特征均值
total_aver[j]/=learning_num
for label in range(K):
P_t[label]=total[label]/learning_num # 求先验概率
for j in range(feature_num):
aver[label][j]/=total[label] # 求每种样本的特征均值
for i in range(learning_num): # 计算样本标准差
label=y_train[i]
for j in range(feature_num):
sigma[label][j]+=(aver[label][j]-x[i][j])**2
total_sigma[j]+=(total_aver[j]-x[i][j])**2
for j in range(feature_num):
total_sigma[j]=(total_sigma[j]/learning_num)**(0.5) # 得到所有样本的某个特征的标准差
for label in range(K):
for j in range(feature_num):
sigma[label][j]=(sigma[label][j]/total[label])**(0.5) # 得到对于每种样本的标准差
# 对测试集进行验证
def pro(i,t,r): # 概率分布函数,对于第i个测试样本t类别r特征
global aver, sigma
if sigma[t][r]<10**(-16): # 注意这里的精度问题
if aver[t][r]-y[i][r]<10**(-16):
return 1
else:
return 0
if ((np.sqrt(2*np.pi)*sigma[t][r])*np.exp(-(y[i][r]-aver[t][r])/(2*(sigma[t][r]**2))))<10**(-50):
if aver[t][r] - y[i][r] < 10 ** (-16):
return 1
else:
return 0
else:
return 1/(np.sqrt(2*np.pi)*sigma[t][r])*np.exp(-(y[i][r]-aver[t][r])/(2*(sigma[t][r]**2))) # 服从正态分布
def Pro(i,r): # 概率分布函数,对于第i个测试样本所有样本r特征
global total_aver, total_sigma
if total_sigma[r]<10**(-16): # 注意这里的精度问题
if total_aver[r]-y[i][r] < 10**(-16):
return 1
else:
return 0
if (np.sqrt(2*np.pi)*total_sigma[r])*np.exp(-(y[i][r]-total_aver[r])**2/(2*(total_sigma[r]**2)))<10**(-50):
if total_aver[r] - y[i][r] < 10 ** (-16):
return 1
else:
return 0
else:
return 1/(np.sqrt(2*np.pi)*total_sigma[r])*np.exp(-(y[i][r]-total_aver[r])**2/(2*(total_sigma[r]**2))) # 服从正态分布
acc=0 # 精确度
for i in range(testing_num): # 测试集遍历
_class=0 # 最终分裂结果
max_D=1.0 # 最大分类概率
max_D_digit=-10000000 # 手动科学计数法 实际是 D*10^(D_digit)
for label in range(K): # 每一个特类别
D=1 # 实数位
D_digit=0 # 暂存位数
D*=P_t[label]
for r in range(feature_num): # 每一个特征
D*=pro(i,label,r) # 分子的累乘正态分布部分
# D/=Pro(i,r) # 分母的累乘正态分布部分
while D<1 and D!=0: # 由于精度问题手动改为科学计数法
D*=10
D_digit-=1
while D>=10 and D!=0:
D/=10
D_digit+=1
if D_digit>max_D_digit or (D_digit==max_D_digit and D>max_D): # argmax_label D
max_D=D
max_D_digit=D_digit
_class=label
print(label,"->",D,"*10^",D_digit)
print(y_test[i]," : ",_class)
if _class==y_test[i]: # 标签分类正确
acc+=1
print("")
print(acc/testing_num*100,end="%") # 计算准确率
这里最终的所有的数据都被归类为了1。经过分析,1 所占的面积最小,而均值一般也是一个比较小的数字,所以0对于任意特征的先验概率都属于一个比较大的值,最终所有的测试样本都被归为了1。这里是没有经过数值可视化观察就直接照抄书本范的错误。
对于60000个样本的某个特征像素值分布如下:
label=2 feature=155 一般的图像中间值情况

label=8 feature=555 一般的图像外边情况

label=3 feature=425 一般的图像边缘情况
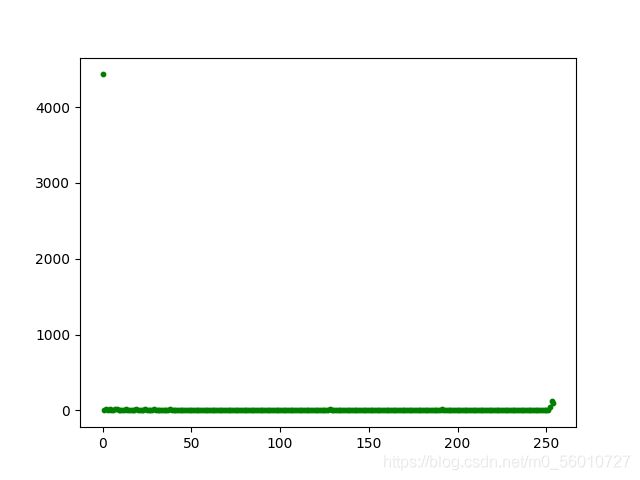
根据上面对于某一个特征可视化后,可以看出强行正态分布是多么愚蠢。所以不要强行正态分布!不要强行正态分布!不要强行正态分布!
3.视作离散型数值预处理以及先验概率计算
经过上面的特征可视化,其实大部分的特征基本可以确定数值几乎都是在0与255周围,所以简单的视作离散型变量。分成三个类别:0,(0,125],(125,255]就足够了。先验概率的计算简单的进行三种情况的归类即可。
经过了所有的预处理,则很容易就可以实现朴素贝叶斯手写数字识别的代码了。此处可以添加一个PCA降维方法进行降维,但是784个特征60000个样本实际上在可以接受的范围内,所以此处不降维。另一个降维的方法均值池化可能减少一些位置差异造成的信息损失。但是这里就不讨论了。
Python3代码如下,朴素贝叶斯
import numpy as np
feature_num=784 # 总特征数
learning_num = 60000 # 学习样本数
testing_num = 1000 # 测试样本数
K = 10 # 总类别数
N = 60000 # 总样本数
pca_num = 3 # 压缩特征维度
data = np.load("mnist.npz")
x_train = data['x_train'] # 学习集集图像
y_train = data['y_train'] # 学习集标签
x_test = data['x_test'] # 测试集图像
y_test = data['y_test'] # 测试集标签
# 读入训练集与测试集样本
x=np.zeros((learning_num,feature_num)) # 学习样本
for i in range(learning_num):
for j in range(feature_num):
x[i][j]=x_train[i][j//28][j%28] # 样本向量化
y=np.zeros((testing_num,feature_num)) # 测试样本
for i in range(testing_num):
for j in range(feature_num):
y[i][j] = x_test[i][j // 28][j % 28] # 样本向量化
# 初始化先验概率
total=np.zeros((K,1)) # 每种标签数量
P_t=np.zeros((K,1)) # 10个类别的样本数目概率
pro=np.zeros((3,K,feature_num)) # 对于三种情况,对于10个样本,每个特征出现的概率
for i in range(learning_num):
label=y_train[i]
total[label]+=1
for j in range(feature_num): # 三种情况分别处理
if x[i][j]==0:
pro[0][label][j]+=1
elif x[i][j]<=125:
pro[1][label][j]+=1
else :
pro[2][label][j]+=1
for i in range(3):
for label in range(K):
for j in range(feature_num):
pro[i][label][j]/=total[label] # 求先验概率
for label in range(K):
P_t[label]=total[label]/learning_num # 求先验概率
# 对测试集进行验证
acc=0 # 精确度
for i in range(testing_num): # 测试集遍历
_class=0 # 最终分裂结果
max_D=1.0 # 最大分类概率
max_D_digit=-10000000 # 手动科学计数法 实际是 D*10^(D_digit)
for label in range(K): # 每一个特类别
D=1 # 实数位
D_digit=0 # 暂存位数
D*=P_t[label]
for r in range(feature_num): # 每一个特征
if y[i][r]==0:
D*=pro[0][label][r] # 分情况讨论
elif y[i][r]<=125:
D*=pro[1][label][r]
else:
D*=pro[2][label][r]
while D<1 and D!=0: # 由于精度问题手动改为科学计数法
D*=10
D_digit-=1
while D>=10 and D!=0:
D/=10
D_digit+=1
if D==0:
D_digit=-10000000
break
if D_digit>max_D_digit or (D_digit==max_D_digit and D>max_D): # argmax_label D
max_D=D
max_D_digit=D_digit
_class=label
if _class==y_test[i]: # 标签分类正确
acc+=1
print(acc/testing_num*100,end="%") # 计算准确率
最终依靠这套参数可以跑出83%左右的正确率,且运行开销也比较小,时间复杂度较低,思路比较简单,优于其他分类器的一点是最终可以给出一个明确的概率。
无监督学习
K-means聚类的实现
一次失败的教训:高中的一个午后,我在学校旁边的新华书店找到了一本机器学习算法的书籍。当时就很容易的学习了简单的K-means聚类算法。开始跟随自己的老师学习写周报的时候,自以为已经完全掌握了K-means的原理,随即想当然的使用了图像样本直接做差求矩阵二范数的方式来表示距离,进行K-means的求解。最终效果极差,而这也是因为直接使用l-2范数没有进行其它操作,或l-p范数并不适合图像处理的结果。
直接转化为0-1图像使用二范数进行图像距离对比的失败案例,Python3代码如下:
import numpy as np
from random import *
learning_num = 60000 # 学习样本数
K = 10 # 分类
N = 60000 # 总样本
data = load("mnist.npz")
x_train = data['x_train'] # 60000数据集
belong = [0 for i in range(N)]
# 0->5 1->0 2->4 3->1 4->9 5->2 6->1 7->3 8->1 9->4 10->3 11->5 12->3 13->6 14->1 15->7
y_train = data['y_train'] # 60000数据集
x_test = data['x_test'] # 10000数据集
y_test = data['y_test'] # 10000数据集
def classification(): # 归类并判断是否归类成功
global centre
finish = True
for i in range(0, learning_num): # 确定归属
previous_belong = belong[i] # 保存之前的归属
min_i = 100000
for j in range(0, 10):
distance = dis(fig[i], centre[j])
if distance > min_i:
belong[i] = j
min_i = distance
if belong[i] != previous_belong: # 归属有变,说明未归类完成
finish = False
if finish == True: # 迭代结束
return finish
num = [0 for k in range(0, 10)] # 每个簇的个体数
centre = [[0 for k in range(28 * 28)] for k in range(0, 10)] # 每个簇清零
for i in range(learning_num): # 重新确定聚类中心
num[belong[i]] += 1
for j in range(28 * 28):
centre[belong[i]][j] += fig[i][j]
for i in range(10):
for j in range(28 * 28):
centre[i][j] /= num[i]
return finish # 迭代继续
def init_centre(): # 初始化中心点
for i in range(K):
for j in range(0, 28 * 28):
centre[i].append(randint(0, 1)) # 随机初始化起始点
def print_centre(): # 打印中心点
for i in range(10):
print("1")
show_fig(centre[i])
print("")
def dis(a, b): # 距离函数
sum = 0
for i in range(0, 28 * 28):
sum += (a[i] - b[i]) ** 2
return sum
def show_fig(a): # 在编译器中展示数据
p = 0
for i in range(0, 28):
for j in range(0, 28):
if (a[p] >= 0.5):
print('*', end=' ')
else:
print(' ', end=' ')
p += 1
print("\n")
def belong_to(a): # 判断新数据属于哪个簇
c = 0
res = [0 for i in range(28 * 28)] # 图像格式化
for i in range(0, 28):
for j in range(0, 28):
r = int(a[i][j]) # 将图像转为黑白
if (r):
res[c] = 1
else:
res[c] = 0
c += 1
c = 1
for i in range(10):
if dis(centre[i], res) < dis(centre[c], res):
c = i
return res, c
fig = [[0 for col in range(28 * 28)] for num in range(0, N)]
p = -1
for k in x_train: # 学习x_train 中内容
p += 1 # 先训练四千个试试
if p > learning_num:
break
c = 0
for i in range(0, 28):
for j in range(0, 28):
r = int(k[i][j]) # 将图像转为黑白
if (r):
fig[p][c] = 1
else:
fig[p][c] = 0
c += 1
centre = [[] for i in range(K)]
init_centre()
while classification() == False:
continue
out_file = open("ResultOfKNN.txt", "w")
for belong_num in range(10):
print("group " + str(belong_num), end='\n\n\n', file=out_file)
for i in range(100):
k = x_train[i]
res, b = belong_to(k)
if b == belong_num:
p = 0
for i in range(0, 28):
for j in range(0, 28):
if (res[p] >= 0.5):
print('*', end=' ', file=out_file)
else:
print(' ', end=' ', file=out_file)
p += 1
print("\n", file=out_file)
print("\n\n", file=out_file)
out_file.close()
虽然正确使用了K-means的框架,但是由于对于图像距离度量的方式有严重问题,最终的正确率几乎为10%(即此模型完全无效)。调试了多次参数,最终将K设置为16的时候大约能达到15%的正确率,证明图形度量方式并非完全无效。
经过分析,样本矩做差求矩阵二范数有着严重的缺陷:假设同一个图像,仅仅图像有少许位置偏移,或者大小改变,则算出来的结果甚至比不同数字的样本间差距极其巨大。而且最后发现得到的结果基本都被归为了0这一类。假设我在盲目代码实现之前进行这样一个小小的测试,就不会出现这样的错误了。但是这样的经历也是对于科研精神培养有着较好的促进作用。
1.总论
K-means是最简单的一种无监督学习方法,其本质是通过不断的迭代找寻K个簇,将所有样本分配到其中。对于手写数字识别,确立基本的K=10,即最终需要将所有数字样本分类到10个簇中。随机初始化这是个簇的中心点,然后对于每一个样本到每个中心点的距离进行计算,求出距离最近的点并且归入这个簇。完成所有样本的分类后,每个簇重新计算中心点均值。按照上述方式进行迭代,直至每个簇的中心点不再移动,即迭代收敛。可以证明对于任意的样本最终簇的中心一定收敛。K-means的基本思想较为简单,关键点在于样本的预处理以及距离度量的方式选取。
2.K-means的实现
已经证明,矩阵做差求l-p范数方式由于不同手写图像风格极大的差异,效果并不理想。在斯坦福CS231公开课找到了这样一种解决模式,实际上是CV的基础部分。下面的链接粗略引入KNN在图像处理中的应用,也提到了此处K-means同样遇到的图像距离估计的一些模式问题,但是没有给出具体的解答。上文中KNN已经提出了PCA方法进行降噪处理,并且尽量可视化以及尝试保留主成分观察是否可分,并且求得自适应距离度量方式。此处不做与上文重复的工作,仅仅使用l-1范数(效果稍好)对K-means进行一个参数K调试的观察。
l-1范数的K-means代码如下:
分析总结及一些思考
手写数字识别的总结
根据某位数学老师引用的某位AI大师的话:一切AI算法都是函数拟合。对这句话的理解在上述的算法中也有着体现:神经网络是将数据点使用任意形式的高维曲面进行拟合;SVM是将低维度的数据点投射到更高维度,然后在更高维度使用超平面进行拟合;决策树以及随机森林本质上是使用了无数的高维立方体一样的区间,将不同标签的数据进行分割;K-means和KNN在一定程度上都是找到一些中心点,根据适应与数据集的距离定义方式进行中心点各自占领离它们最近的空间……其余的一些算法或许略有差异,然而本质上都与函数拟合有着一定的关联。
关于几种算法的实验结果如下:
| 算法名称 | 学习样本数 | 特征数 | 控制参数 | 环境及耗时 | 准确率 |
|---|---|---|---|---|---|
| ANN | 10000 | 784 | 3000轮 隐藏层 2 × 20 2\times20 2×20个神经元 | CPP:20min | 92% |
| CNN | |||||
| Naive-Bayes | 60000 | 784 | 分界点为0,125,255 | Python3:3min | 83% |
| KNN+PCA | 5000 | 100 | 自适应图像距离度量 | ||
| SVM(sklearn) | 60000 | 784 | 高斯核函数 | Python:8min | 98% |
| Decision-Tree | 1500 | 100 | 15层 信息熵规划 | CPP:3min | 32% |
| Random-Forest | 2000 | 100 | 15层 信息熵规划 20棵树 | CPP:3min | 83% |
| Random-Forest(sklearn) | 60000 | 784 | 20层 信息熵规划 20棵树 | Python:1min | 96% |
| K-means | 60000 | 784 | l-2范数 0-1图像形式 K=16 | Python3::5min | 15% |
很悲伤,我被sklearn和Torch完美的暴打了。自己造的三轮车怎么比得上全球顶级科学家一起造的F-1方程式啊……
一些感想
我很幸运得以生活在这样一个科技飞速发展的时代,并且对AI这一具备伟大发展潜力的领域拥有天然的极大的兴趣。我看到身边的同学或对未来充满无限的憧憬,期待着有一天能够去到国内外顶级名校实现人生梦想,亦看到早在大一就因为近年算法岗竞争太过激烈从此转向前端开发、软件工程等的同学;我看到有诸多如我自己一般由于怀揣巨大的面向世界野心,却并未拥有与之相匹配的能力而痛苦者,也看到诸多追求平凡,仅仅希望不那么拼命而将人生以慢节奏方式度过而悠然者。每个人自然有他们的选择,多年后回首,或许今天诸多选择的差异也并没有那么巨大的影响,不过每个人在自己选择的道路上不断前行,实践着自己对人生的理解。
正如雪莱的《奥西曼提斯》中描绘的一切功业皆归为尘土,然而为现世的为“万王之王”的野心并不因此改变。今日我们前行的路,通向所不可预见的远方,但是我们依然坚定的走下去,凭着青春的野心与无限的热爱!