算法学习—利用Python解决多元线性回归数据统计
由于准备参加数学建模比赛,最近在CSDN上看了不少关于利用Python来完成对数据多元线性回归的资料,想利用这篇博客进行一下总结与回顾:
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。事实上,一种现象常常是与多个因素相联系的,由多个自变量的最优组合共同来预测或估计因变量,比只用一个自变量进行预测或估计更有效,更符合实际。因此多元线性回归比一元线性回归的实用意义更大。
在进行数据导入之前需要导入的包:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
其中NumPy(Numerical Python)是Python的一种开源的数值计算扩展。这种工具可用来存储和处理大型矩阵,比Python自身的嵌套列表(nested list structure)结构要高效的多(该结构也可以用来表示矩阵(matrix)),支持大量的维度数组与矩阵运算,此外也针对数组运算提供大量的数学函数库。
pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。Pandas 纳入了大量库和一些标准的数据模型,提供了高效地操作大型数据集所需的工具。pandas提供了大量能使我们快速便捷地处理数据的函数和方法。
Matplotlib 是一个 Python的2D绘图库,它以各种硬拷贝格式和跨平台的交互式环境生成出版质量级别的图形,在我之前的博客中也多次用到过它。
seaborn是在matplotlib基础上进行封装,Seaborn就是让困难的东西更加简单。用Matplotlib最大的困难是其默认的各种参数,而Seaborn则完全避免了这一问题。
接着,我们利用数据集 Advertising.csv,其数据描述了一个产品的销量与广告媒体的投入之间影响。这个数据集在很多关于利用Python完成多元线性回归的帖子中都被用到:
首先,我们利用pandas的pd.read()来读取数据:
#通过read_csv来读取我们的目的数据集
adv_data = pd.read_csv('Advertising.csv')
然后对数据进行相关性分析,以此来查找数据中特征值与标签值之间的关系:
![]()
print(adv_data.corr())#对数据进行相关性分析,以此来查找数据中特征值与标签值之间的关系
可以从corr表中看出,TV特征和销量是有比较强的线性关系的,而Radio和Sales线性关系弱一些但是也是属于中等程度相关的,而Newspaper和Sales线性关系更弱(0~0.3 弱相关,0.3~0.6 中等程度相关,0.6~1 强相关):
在建立模型的第一步我们将建立训练集与测试集,会使用train_test_split函数来创建(train_test_split是存在与sklearn中的函数):
X_train,X_test,Y_train,Y_test = train_test_split(adv_data.iloc[:,:3],adv_data.sales,train_size=.80)
print("原始数据特征:",adv_data.iloc[:,:3].shape,
",训练数据特征:",X_train.shape,
",测试数据特征:",X_test.shape)
print("原始数据标签:",adv_data.sales.shape,
",训练数据标签:",Y_train.shape,
",测试数据标签:",Y_test.shape)
建立初步的数据集模型之后将训练集中的特征值与标签值放入LinearRegression()模型中且使用fit函数进行训练,在模型训练完成之后会得到所对应的方程式(线性回归方程式),需要利用函数中的intercept_与coef_:
model = LinearRegression()
model.fit(X_train,Y_train)
a = model.intercept_#截距
b = model.coef_#回归系数
print("最佳拟合线:截距",a,",回归系数:",b)
输出为:
即所得的多元线性回归模型的函数为 : y = 2.813 + 0.045 * tv + 0.192 * Radio + 0.001 * Newspaper。就是说,对于给定了Radio和Newspaper的广告投入,如果在tv广告上每多投入1个单位,对应销量将增加0.045个单位,以此类推。
接下来对模型进行测评。使用score函数来获取所需要的模型得分:
#对模型进行测评
score = model.score(X_test,Y_test)
print(score)
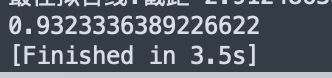
从输出可看出该模型的得分:
还可以使用predict函数来获取所需要的预测值:
#对线性回归进行预测
Y_pred = model.predict(X_test)
print(Y_pred)
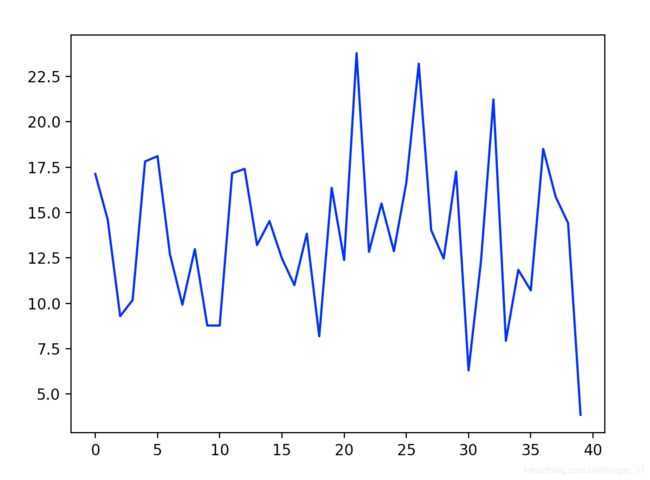
plt.plot(range(len(Y_pred)),Y_pred,'b',label="predict")
#显示图像
plt.savefig("predict.jpg")
plt.show()
可以看到输出为:
下面是整个程序的代码:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from pandas import DataFrame,Series
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
#通过read_csv来读取我们的目的数据集
adv_data = pd.read_csv('Advertising.csv')
print(adv_data.corr())#对数据进行相关性分析,以此来查找数据中特征值与标签值之间的关系
'''在建立模型的第一步我们将建立训练集与测试集,会使用train_test_split函数来创建(train_test_split是存在与sklearn中的函数)'''
X_train,X_test,Y_train,Y_test = train_test_split(adv_data.iloc[:,:3],adv_data.sales,train_size=.80)
print("原始数据特征:",adv_data.iloc[:,:3].shape,
",训练数据特征:",X_train.shape,
",测试数据特征:",X_test.shape)
print("原始数据标签:",adv_data.sales.shape,
",训练数据标签:",Y_train.shape,
",测试数据标签:",Y_test.shape)
#建立初步的数据集模型之后将训练集中的特征值与标签值放入`LinearRegression()`模型中且使用`fit`函数进行训练,在模型训练完成之后会得到所对应的方程式(线性回归方程式),需要利用函数中的`intercept_`与`coef_
model = LinearRegression()
model.fit(X_train,Y_train)
a = model.intercept_#截距
b = model.coef_#回归系数
print("最佳拟合线:截距",a,",回归系数:",b)
#对模型进行测评
score = model.score(X_test,Y_test)
print(score)
#对线性回归进行预测
Y_pred = model.predict(X_test)
print(Y_pred)
plt.plot(range(len(Y_pred)),Y_pred,'b',label="predict")
#显示图像
plt.savefig("predict.jpg")
plt.show()