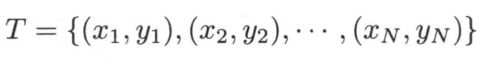统计学习方法第二版 李航

前言

《统计学习方法》和《机器学习》这两本书，大概是做科研的小伙伴都避不开的必读书吧。笔者在很久前就已经学过该书了，但是因为先前学完没有做一个详细的整理总结。然后最近实验室招新，需要带一带小朋友学习这本书，故重温该书且在此整理记录，望对大家有所帮助！

第一章 统计学习及监督学习概论

这一章主要都是些概念，所以我可能更多的内容是会直接照搬原文的内容。

统计学习或机器学习一般包括监督学习、无监督学习、强化学习。有时还包括半监督学习、主动学习。

监督学习与无监督学习可以简单理解为训练时有无label，训练数据x对应有一个label那就是监督学习，无则是无监督学习。

监督学习

监督学习分为学习和预测两个过程，由学习系统与预测系统完成。在学习过程中，学习系统利用给定的训练数据集，通过学习(或训练)得到一个模型，表示为条件概率分布 P(YIX) 或决策函数 = f(X) 。条件概率分布 P(YIX) 或决策函数 f(X)描述输入与输出随机变量之间的映射关系。在预测过程中，预测系统对于给定的测试样本集中的输入XN+l’ 由模型
给出相应的输出 YN+l。

学习系统(也就是学习算法)试图通过训练数据集中的样本 (Xi Yi) 带来的信息学习模型。具体地说，对输入叭，一个具体的模型 f(x) 可以产生 个输出 f(Xi)'而训练数据集中对应的输出是仇。如果这个模型有很好的预测能力，训练样本输出 Yi和模型输出 f(Xi) 之间的差就应该足够小。学习系统通过不断地尝试，选取最好的模型，以便对训练数据集有足够好的预测，同时对未知的测试数据集的预测也有尽可能好的推广。

无监督学习

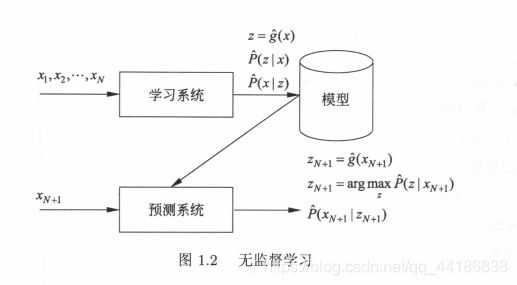
无监督学习可以用于对己有数据的分析，也可以用于对未来数据的预测。分析时使用学习得到的模型，即函数 = g(x) 条件概率分布户(z x) 或者条件概率分布 P(xlz) 。预测时，和监督学习有类似的流程 由学习系统与预测系统完成，如图1. 3所示。在学习过程中，学习系统从训练数据集学习，得到→个最优模型，表示为函数 Z=g(x) 条件概率分布户(zlx) 或者条件概率分布户(xlz) 。在预测过程中，预测系统对于给定的输入 XN+l
给出相应的输出 ZN+l’进行聚类或降维，或者由模型户(xlz) 给出输入的概率P(xN+1 | ZN+1) 进行概率估计。

强化学习

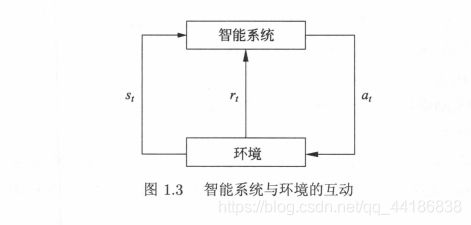
智能系统与环境的互动如图1. 所示。在每 智能系统从环境中观测到状态 （state) St 个奖励 (reward) ru 采取 1个动作 (action) 句。环境根据智能系统选择的动作，决定下 t+l 的状态 t+1 与奖励 rt+l 要学习的策略表示为给定的状态下采取的动作。智能系统的目标不是短期奖励的最大化，而是长期累积奖励的最大化 强化学习过程中，系统不断地试错 (trial and error) ，以达到学习最优策略的目的。

感觉自己强化学习这一块估计会很少接触，所以看得时候也只是看个大概。

按模型分类

上面是统计学习的基本分类，按模型分类的话，可以分成概率模型和非概率模型，线性模型和非线性模型，以及参数模型和非参数模型。

按算法分类

按算法分类的话，可以分为在线学习 (online learning) 与批量学习 (batch learning) 。

在线学习是指每次接受 个样本，进行预测，之后学习模型，并不断重复该操作的机器学习。与之对应，批量学习 次接受所有数据，学习模型，之后进行预测。

在线学习通常比批量学习更难，很难学到预测准确率更高的模型，因为每次模型更新中，可利用的数据有限。

按技巧分类

1.贝叶斯学习

贝叶斯学习 CBayesian learning) ，又称为贝叶斯推理 CBayesian inference) ，是统计学、机器学习中重要的方法。其主要想法是，在概率模型的学习和推理中，利用贝叶斯定理，计算在给定数据条件下模型的条件概率，即后验概率，并应用这个原理进行模型的估计，以及对数据的预测。将模型、未观测要素及其参数用变量表示，使用模型的先验分布是贝叶斯学习的特点。贝叶斯学习中也使用基本概率公式(图1.4)。朴素贝叶斯、潜在狄利克雷分配的学习属于贝叶斯学习。

贝叶斯估计与极大似然估计在思想上有很大的不同，代表着统计学中频率学派和贝叶斯学派对统计的不同认识。其实，可以简单地把两者联系起来，假设先验分布是均匀分布，取后验概率最大，就能从贝叶斯估计得到极大似然估计。

2. 核方法

核方法 (kernel method) 是使用核函数表示和学习非线性模型的一种机器学习方法，可以用于监督学习和无监督学习。有一些线性模型的学习方法基于相似度计算，更具体地，向量内积计算。核方法可以把它们扩展到非线性模型的学习，使其应用范围更广泛。

核函数支持向量机，以及核 PCA 、核 均值属于核方法。

把线性模型扩展到非线性模型，直接的做法是显式地定义从输入空间(低维空间)到特征空间(高维空间)的映射，在特征空间中进行内积计算。

统计学习方法三要素

统计学习方法都是由模型、策略和算法构成的，即统计学习方法由 要素构成，可以简单地表示为:

方法=模型+策略+算法

这里的话我就简单说明一下就好了。

模型：选啥模型，简单理解就是选择什么样的函数，比方说感知机用的就是 f(x) = sign(ω*x + b)，knn用的是求取欧式度量，进而建立树来回溯。

策略：简单来说，就是建立模型的时候，怎么表示我预测的和真实的之间的误差大小。比方说0-1损失函数，你预测对了为1，错了为0，我损失了多少这个时候看的就是我有多少个0。（当然了，一般也不用这个损失函数，下文会讲）

算法：存在的作用就是用来求出，什么时候（模型参数为多少时）给的策略给的损失最小。对应上面说的0-1损失函数，那就是求出啥时候0最少，1最多。

模型评估与模型选择

这一部分我想着重讲一下！

1. 训练误差与测试误差

统计学习的目的是使学到的模型不仅对己知数据而且对未知数据都能有很好的预测能力。不同的学习方法会给出不同的模型。当损失函数给定时，基于损失函数的模型的训练误差 Ctraining error) 和模型的测试误差 test error) 就自然成为学习方法评估的标准。注意，统计学习方法具体采用的损失函数未必是评估时使用的损失函数（不过一般都是）。

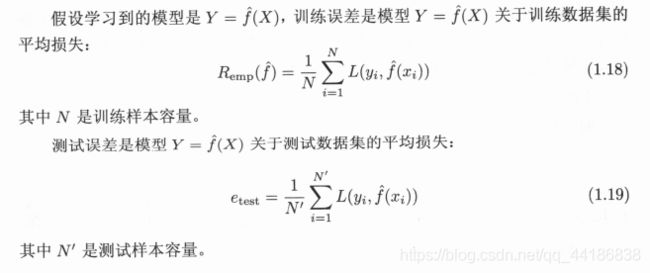
训练误差的大小，对判断给定的问题是不是 个容易学习的问题是有意义的，但本质上不重要。测试误差反映了学习方法对未知的测试数据集的预测能力，是学习中的重要概念。显然，给定两种学习方法，测试误差小的方法具有更好的预测能力，是更有效的方法。通常将学习方法对未知数据的预测能力称为泛化能力 (generalization ability)。

2. 过拟合与模型选择

过拟合简单来说就是此时的模型对于你自己的训练数据的预测结果极好，但是往往对于未知的数据效果不太行。

当假设空间含有不同复杂度(例如，不同的参数个数)的模型时，就要面临模型选择(model selection) 的问题。我们希望选择或学习 个合适的模型。如果在假设空间中存在"真"模型，那么所选择的模型应该逼近真模型。具体地，所选择的模型要与真模型的参数个数相同，所选择的模型的参数向量与真模型的参数向量相近。

如果一味追求提高对训练数据的预测能力，所选模型的复杂度则往往会比真模型更高。这种现象称为过拟合 Cover-fitting) 。过拟合是指学习时选择的模型所包含的参数过多，以至出现这 模型对己知数据预测得很好，但对未知数据预测得很差的现象。可以说模型选择旨在避免过拟合并提高模型的预测能力。

具体避免模型过拟合的方法可以参考：https://www.cnblogs.com/june0507/p/7600924.html

正则化与交叉验证

1. 正则化

模型选择的典型方法是正则化 (regularization) 。正则化是结构风险最小化策略的实现，是在经验风险上加 个正则化项 (regularizer )或罚项 (penalty term) 。正则化项 般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。比如，正则化项可以是模型参数向量的范数。

正则化的作用是选择经验风险与模型复杂度同时较小的模型。

2. 交叉验证

交叉验证，其实本质就是用来求取模型给的超参数，可用于降低模型的过拟合效果。

如果给定的样本数据充足，进行模型选择的一种简单方法是随机地将数据集切分成三部分，分别为训练集 (training set) 、验证集 (validation set) 和测试集 (testset) 。训练集用来训练模型，验证集用于模型的选择，而测试集用于最终对学习方法的评估。在学习到的不同复杂度的模型中，选择对验证集有最小预测误差的模型。由于验证集有足够多的数据，用它对模型进行选择也是有效的。

但是，在许多实际应用中数据是不充足的。为了选择好的模型，可以采用交叉验证方法。交叉验证的基本想法是重复地使用数据; 把给定的数据进行切分，将切分的数据集组合为训练集与测试集，在此基础上反复地进行训练、测试以及模型选择。

1.简单交叉验证
简单交叉验证方法是:首先随机地将己给数据分为两部分， 部分作为训练集，另一部分作为测试集(例如， 70% 的数据为训练集， 30% 的数据为测试集) ;然后用训练集在各种条件下(例如，不同的参数个数)训练模型，从而得到不同的模型:在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

2 . S折交叉验证
应用最多的是S折交叉验证，方法如下：首先随机地将已给数据切分为互不相交、大小相同的子集；然后利用 S-1个子集的数据训练模型，利用 余下的子集测试模型 ；将这一过程对可能的选择重复进行；最后选出S次评测中平均测试误差最小的模型。

3.留一交叉验证
S折交叉验证的特殊情形是S = N, 称为留一交叉验证 (leave-one-out cross validation) ，往往在数据缺乏的情况下使用。这里 N是给定数据集的容量。

泛化能力

学习方法的泛化能力 (generalization ability) 是指由该方法学习到的模型对未知数据的预测能力，是学习方法本质上重要的性质。现实中采用最多的办法是通过测试误差来评价学习方法的泛化能力。但这种评价是依赖于测试数据集的。因为测试数据集是有限的，很有可能由此得到的评价结果是不可靠的。统计学习理论试图从理论上对学习方法的泛化能力进行分析。

泛化误差

泛化误差反映了学习方法的泛化能力，如果 种方法学习的模型比另 种方法学习的模型具有更小的泛化误差，那么这种方法就更有效。事实上，泛化误差就是所学习到的模型的期望风险。

泛化误差上界

学习方法的泛化能力分析往往是通过研究泛化误差的概率上界进行的，简称为泛化误差上界（generalization error bound) 。具体来说，就是通过比较两种学习方法的泛化误差上界的大小来比较它们的优劣。泛化误差上界通常具有以下性质:它是样本容量的函数，当样本容量增加时，泛化上界趋于 0; 它是假设空间容量 （capacity)函数，假设空间容量越大，模型就越难学，泛化误差上界就越大。

生成模型与判别模型

监督学习方法又可以分为生成方法 Cgenerative approach) 和判别方法 discriminative approach) 所学到的模型分别称为生成模型 (generative model)和判别模型(discriminative model)

在监督学习中，生成方法和判别方法各有优缺点，适合于不同条件下的学习问题。

生成方法的特点：生成方法可以还原出联合概率分布 P(X Y) 而判别方法则不能:生成方法的学习收敛速度更快，即当样本容量增加的时候，学到的模型可以更快地收敛于真实模型:当存在隐变量时，仍可以用生成方法学习，此时判别方法就不能用。

判别方法的特点：判别方法直接学习的是条件概率 P(YIX) 或决策函数 f(X)直接面对预测，往往学习的准确率更高:由于直接学习 P(YIX) f(X) 可以对数据进行各种程度上的抽象、定义特征并使用特征，因此可以简化学习问题。

监督学习的应用

监督学习的应用主要是三个方面：分类问题、回归问题和标注问题。

具体可以参考：https://www.cnblogs.com/kklalala-kaly/p/12169652.html

模型评估的各项指标

模型好不好，就看它预测未知数据准不准咯。那就不多bb，直接介绍。

以一个二分类问题为例，样本有正负两个类别。

那么模型预测的结果和真实标签的组合就有4种：TP，FP，FN，TN。

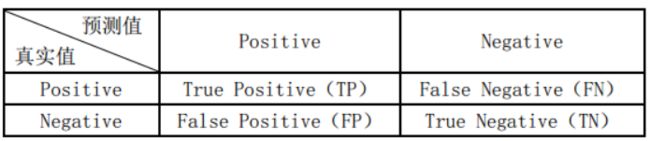
TP实际为正样本，预测为正样本；
FN实际为正样本，预测为负样本；
FP实际为负样本，预测为正样本；
TN实际为负样本，预测为负样本。
（其实T就是true，F就是false，P就是positive，N就是negative）

Accuracy(准确率)

简单讲，就是预测对的样本数占样本总数的比例。正确的样本数是TP,TN；总体的样本数就是：TP+FN+FP+TN。
所以根据定义，可以得到Acc的计算公式：

Accuracy = TP+TN / (TP+TN+FP+FN)

Precision(精确率)
精确率又称查准率，简单讲就是预测为正的样本中有多少是真正的正样本。

公式：
Precision = TP / (TP+FP)

召回率(Recall)
召回率又叫查全率，简单讲就是样本中的正例有多少被预测正确了。

公式：
Recall = TP / (TP+FN)

F1-score
考虑了两种指标的值，用来权衡precision和recall的值。

公式：
F1score = 2∗Precision∗Recall / (Precision+Recall)

第二章 感知机

导论

感知机 (perceptron) 是二类分类的线性分类模型,其输入为实例的特征向量,输 出为实例的类别，取 +1 和-1值.感知机对应于输入空间(特征空间)中将实例划分为正负两类的分离超平面,属于判别模型。感知机学习旨在求出将训练数据进行线性划分的分离超平面，为此，导入基于误分类的损失函数，利用梯度下降法对损失函 数进行极小化，求得感知机模型。感知机学习算法具有简单而易于实现的优点，分为原始形式和对偶形式 。感知机预测是用学习得到的感知机模型对新的输入实例进行分类。感知机1957 年由 Rosenblatt 提出，是神经网络与支持向量机的基础。

定义

感知机是根据输入实例的特征向 对其进行 类分类的线性分类模型： f(x) = sign(ω*x + b)

其中，ω和b为感知机模型参数， ωεR 叫作权值 (weight) 或权值向量( weight vector ), 叫作偏值( bias )， ω*x表示ω和x的内积，sign 是符号函数，当x>=0，sign(x) = 1，当x<0，sign(x) = -1。

感知机模型对应于输入空间(特征空间)中的分离超平面 w*x+b=0

感知机有如下几何解释：线性方程 ω*x + b = 0
对应于特征空间Rn 中的一个超平面， 其中ω是超平面的法向量，b是超平面的截距。这个超平面将特征空间划分为两个部分。位于两部分的点(特征向量)分别被分为正、负两类。因此，超平面S被称为分离超平面 (separating hyperplane) ，如图 2.1 所示。

学习策略

感知机学习的策略是极小化损失函数：minL(w, b) = -\Sigma{y_{i}(ω*x_{i} + b)}

损失函数对应于误分类点到分离超平面的总距离。

学习算法

感知机学习算法是基于随机梯度下降法的对损失函数的最优化算法，有原始形式和对偶形式。算法简单且易于实现 。原始形式中，首先任意选取一个超平面，然后用梯度下降法不断极小化目标函数。在这个过程中一次随机选取一个误分类点使其梯度下降。

收敛性

当训练数据集线性可分时，感知机学习算法是收敛的。感知机算法在训练数据集上的误分类次数 满足不等式:

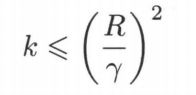
当训练数据集线性可分时，感知机学习算法存在无穷多个解，其解由于不同的初值或不同的迭代顺序而可能有所不同。

实现代码

class Model:
    def __init__(self):
        self.w = np.ones(len(data[0])-1, dtype=np.float32)
        self.b = 0
        self.l_rate = 0.1
        # self.data = data

    def sign(self, x, w, b):
        y = np.dot(x, w) + b
        return y

    # 随机梯度下降法
    def fit(self, X_train, y_train):
        is_wrong = False
        while not is_wrong:
            wrong_count = 0
            for d in range(len(X_train)):
                X = X_train[d]
                y = y_train[d]
                if y * self.sign(X, self.w, self.b) <= 0:
                    self.w = self.w + self.l_rate*np.dot(y, X)
                    self.b = self.b + self.l_rate*y
                    wrong_count += 1
            if wrong_count == 0:
                is_wrong = True
        return 'Perceptron Model!'

    def score(self):
        pass

下载训练数据：

import pandas as pd
import numpy as np
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target

df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
df.label.value_counts()

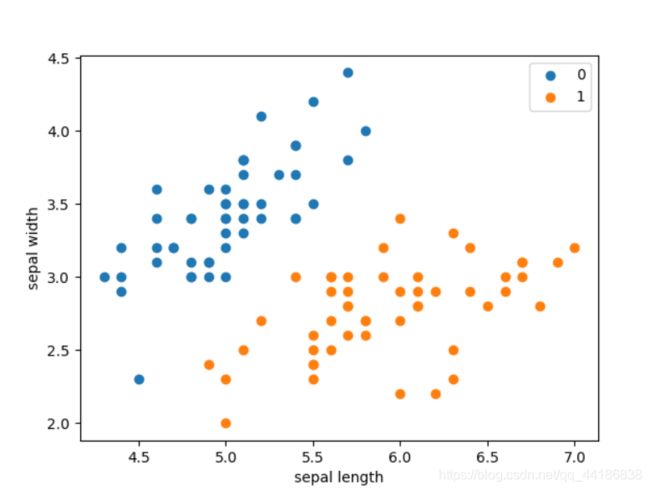
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

data = np.array(df.iloc[:100, [0, 1, -1]])

X, y = data[:,:-1], data[:,-1]

y = np.array([1 if i == 1 else -1 for i in y])

perceptron = Model()
perceptron.fit(X, y)

测试：

x_points = np.linspace(4, 7,10)
y_ = -(perceptron.w[0]*x_points + perceptron.b)/perceptron.w[1]
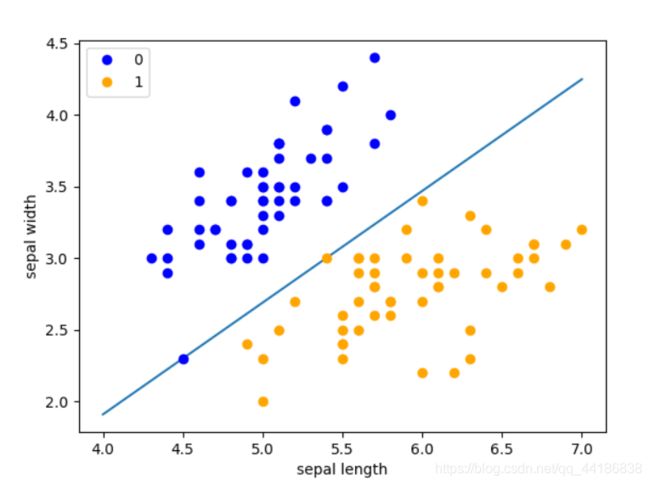
plt.plot(x_points, y_)

plt.plot(data[:50, 0], data[:50, 1], 'bo', color='blue', label='0')
plt.plot(data[50:100, 0], data[50:100, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

第三章 k近邻法

定义

近邻法 (k-nearest neighbor,k -NN) 种基本分类与回归方法。本书只讨论分类问题中的 k近邻法。 近邻法的输入为实例的特征向量，对应于特征空间的点:输出为实例的类别，可以取多类。 近邻法假设给定 个训练数据集， 其中的实例类别己定。分类时，对新的实例，根据其 个最近邻的训练实例的类别，通过多数表决等方式进行预测 因此 近邻法不具有显式的学习过程。

多数表决简单理解即为哪种类别数量多对应的分类结果就是哪种。

而不显式学习简单理解即为，不像感知机等方法需要预先训练好一个模型，k近邻是每次分类就利用一遍训练集里的数据，

k近邻算法

大致理解的话，先是输入训练集：

输出即为实例x所属的类别。

算法流程大致如下：
（1）先是计算x与训练集中给定数据的距离度量最小的k个数据（这里的距离度量通常是求lp距离，一般为l2，即欧式距离）
（2）根据决策方法即多数表决方法来求出实例x所属类别：

k值的选择

大家肯定都能想到k值的选择必然会对结果产生极大影响，那么k值取大取小对应的会有什么影响呢？
选小了：学习的近似误差会减小，但是估计误差会增大。什么意思呢？就是我对于距离实例x的近似点会非常敏感，那如果刚好我的近似点就是误差点的话，那么我的结果就会出错。这样的话便容易出现过拟合。

选大了：对应的可以减小我的估计误差，但是相对的那些原本不那么近似的点也会被我纳入考量，使得发生错误。同时相对的模型也会变得简单。往极端了想，k值等于我训练集的大小，那岂不是巨简单，直接给出我训练集里面类别占比最大的最可以了，但这样肯定是有很大问题的。

在应用中 一般取 比较小的数值，且通常采用交叉验证法来选取最优的k值。

kd树

书本里面最开始讲得非常生硬，这里我打算结合具体题目来讲。

先附一下题目：


上图其实还没有画完整，我先给它补全。

下面介绍解题步骤：
（1）先建立一个kd树，注意这里的kd树是二叉树。
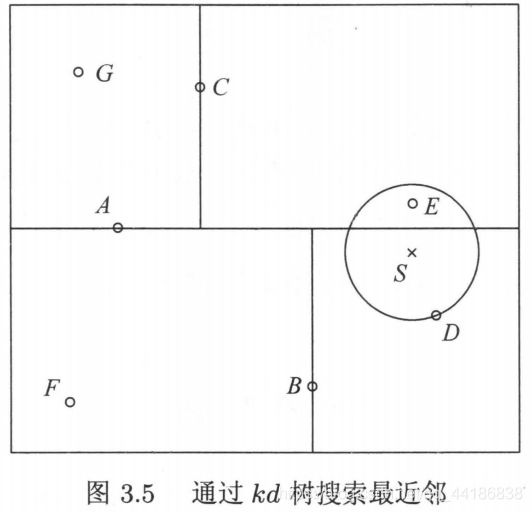
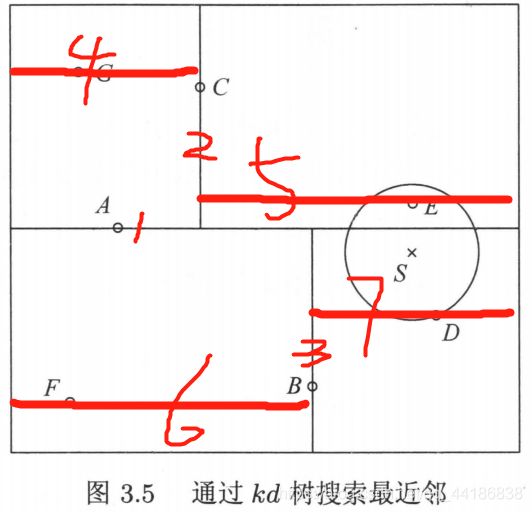
最开始选哪一个作为根节点呢？聪明的小朋友可以发现A是上述的根节点，选它作为根节点的原因是因为它的y坐标大小是所有y坐标大小的中位数。所以我们每次分割的时候都是选其中位数的点（如果中位数的点有两个的话就任一都可）。同样的道理，为啥第二条线不是经过的G或者E，而是经过C（即选C点为子结点），因为C的横坐标大小是在gce点中的中位数。以此类推。
提醒一下啊，我们可以先往x轴方向分割，也可以往y轴方向切割，然后x和y轴方向交替切割。
（2）选择一个叶节点作为“当前最近点”，叶节点上图一共有四个，分别是g、e、f和d点。那为啥选d呢？
是这样子的，实例s点是不是比根节点a的纵坐标要小（之所以比纵坐标是因为这里是从纵坐标开始切割的），既然小的话那我们就选A下面这块区域，这块区域显然是由点B总管的，那这个时候同理再与点B比较一下横坐标，是不是要比点B大，那大的话就选右边这块区域，这个时候显然就只剩下点D了，所以确定点D为当前最近点。
（3）确定完某一个叶节点为当前最近点后，开始递归向上回退，退到父节点B，看看父节点B会不会更近，好的不会，那再看看父节点B它的另一个子区域有没有点比当前最近点还近。具体怎么检查呢，我们以实例点S与当前最近点D的距离为半径画个圆，看看这个区域会不会跟这个圆相交，不会的话就直接放弃，会的话移动到该结点检查是否需要更新当前最近点。
好的，经过上述我们发现点B管的区域也没有用了，那我们再回退到点B的父节点，重复上述工作：即看点A会不会更近，不会，那就看点A的另一个子结点C有没有跟我相交，有，那移动到点C，看看与其相交的右区域有无点包含在圆里面，即距离更近，有，ok，完事。

附原文解释

实现代码

附下实现kd树实现代码：

import numpy as np
from math import sqrt
import pandas as pd
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split

iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']

data = np.array(df.iloc[:100, [0, 1, -1]])
train, test = train_test_split(data, test_size=0.1)
x0 = np.array([x0 for i, x0 in enumerate(train) if train[i][-1] == 0])
x1 = np.array([x1 for i, x1 in enumerate(train) if train[i][-1] == 1])


def show_train():
    plt.scatter(x0[:, 0], x0[:, 1], c='pink', label='[0]')
    plt.scatter(x1[:, 0], x1[:, 1], c='orange', label='[1]')
    plt.xlabel('sepal length')
    plt.ylabel('sepal width')


class Node:
    def __init__(self, data, depth=0, lchild=None, rchild=None):
        self.data = data
        self.depth = depth
        self.lchild = lchild
        self.rchild = rchild


class KdTree:
    def __init__(self):
        self.KdTree = None
        self.n = 0
        self.nearest = None

    def create(self, dataSet, depth=0):
        if len(dataSet) > 0:
            m, n = np.shape(dataSet)
            self.n = n - 1
            axis = depth % self.n
            mid = int(m / 2)
            dataSetcopy = sorted(dataSet, key=lambda x: x[axis])
            node = Node(dataSetcopy[mid], depth)
            if depth == 0:
                self.KdTree = node
            node.lchild = self.create(dataSetcopy[:mid], depth+1)
            node.rchild = self.create(dataSetcopy[mid+1:], depth+1)
            return node
        return None

    def preOrder(self, node):
        if node is not None:
            print(node.depth, node.data)
            self.preOrder(node.lchild)
            self.preOrder(node.rchild)

    def search(self, x, count=1):
        nearest = []
        for i in range(count):
            nearest.append([-1, None])
        self.nearest = np.array(nearest)

        def recurve(node):
            if node is not None:
                axis = node.depth % self.n
                daxis = x[axis] - node.data[axis]
                if daxis < 0:
                    recurve(node.lchild)
                else:
                    recurve(node.rchild)

                dist = sqrt(sum((p1 - p2) ** 2 for p1, p2 in zip(x, node.data)))
                for i, d in enumerate(self.nearest):
                    if d[0] < 0 or dist < d[0]:
                        self.nearest = np.insert(self.nearest, i, [dist, node], axis=0)
                        self.nearest = self.nearest[:-1]
                        break

                n = list(self.nearest[:, 0]).count(-1)
                if self.nearest[-n-1, 0] > abs(daxis):
                    if daxis < 0:
                        recurve(node.rchild)
                    else:
                        recurve(node.lchild)

        recurve(self.KdTree)

        knn = self.nearest[:, 1]
        belong = []
        for i in knn:
            belong.append(i.data[-1])
        b = max(set(belong), key=belong.count)

        return self.nearest, b


kdt = KdTree()
kdt.create(train)
kdt.preOrder(kdt.KdTree)

score = 0
for x in test:
    input('press Enter to show next:')
    show_train()
    plt.scatter(x[0], x[1], c='red', marker='x')  # 测试点
    near, belong = kdt.search(x[:-1], 5)  # 设置临近点的个数
    if belong == x[-1]:
        score += 1
    print("test:")
    print(x, "predict:", belong)
    print("nearest:")
    for n in near:
        print(n[1].data, "dist:", n[0])
        plt.scatter(n[1].data[0], n[1].data[1], c='green', marker='+')  # k个最近邻点
    plt.legend()
    plt.show()

score /= len(test)
print("score:", score)

结束语

正在不断更新中。。。

以后我会在博客记录自己学习《统计学习方法》第二版这本书的笔记，其实也就是我自己认为比较重要或者有用的内容，以及部分python代码的实现。

由于博主能力有限，博文中提及的信息，也难免会有疏漏之处。希望发现疏漏的朋友能热心指出其中的错误，以便下次修改时能以一个更完美更严谨的样子，呈现在大家面前。同时如果有更好的方法也请不吝赐教。

如果有什么相关的问题，也可以关注评论留下自己的问题，我会尽量及时发送！