❤️思维导图整理大厂面试高频数组12: 4种方法彻底解决接雨水问题, 力扣42❤️
此专栏文章是对力扣上算法题目各种方法的总结和归纳, 整理出最重要的思路和知识重点并以思维导图形式呈现, 当然也会加上我对导图的详解.
目的是为了更方便快捷的记忆和回忆算法重点(不用每次都重复看题解), 毕竟算法不是做了一遍就能完全记住的. 所以本文适合已经知道解题思路和方法, 想进一步加强理解和记忆的朋友, 并不适合第一次接触此题的朋友(可以根据题号先去力扣看看官方题解, 然后再看本文内容).
关于本专栏所有题目的目录链接, 刷算法题目的顺序/注意点/技巧, 以及思维导图源文件问题请点击此链接.
想进大厂, 刷算法是必不可少的, 欢迎和博主一起打卡刷力扣算法, 博主同步更新了算法视频讲解 和 其他文章/导图讲解, 更易于理解, 欢迎来看!
文章目录
- 0.导图整理
- 1.了解常规思想
- 2.动态规划 优化时间复杂度
- 3.双指针 优化空间复杂度
- 4.单调栈的思想
- 源码
- Python:
- java:
题目链接: https://leetcode-cn.com/problems/trapping-rain-water/solution/si-wei-dao-tu-zheng-li-4chong-fang-fa-xi-4uua/
0.导图整理
1.了解常规思想
对于本题而言, 首先要掌握最常规的思想, 因为下面的一系列方法大多都是在常规思想上进行的各种优化操作.
但其实本题的常规思想也不是那么容易想的, 看到那分布极不规则的接雨水情况, 对于怎么样将它们求和也并非一样容易的事.
常规思想中最重要的就是 接水量的计算方法 了, 我们采用对于每个下标 i, 分别计算它能够接到的水量, 最后将它们相加在一起.
接下来就是每个下标 i 接水量的计算过程了, 从图中我们可以看出, 一个位置要想接到雨水, 那么两边必然要有比它更高的柱子, 并且下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值, 而下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i].
这就是最重要的接水量的计算过程了, 明白了这个原理之后, 我们只需要分别向左和向右扫描并记录左边和右边的最大高度, 然后计算每个下标位置能接的雨水量.
这就是常规思想的全部思路了, 这个方法会用到两次循环, 时间复杂度就达到了 O ( n 2 ) O(n^2) O(n2), 接下来就是我们的优化过程了.
2.动态规划 优化时间复杂度
上述做法的时间复杂度较高是因为需要对每个下标位置都向两边扫描。如果已经知道每个位置两边的最大高度, 则可以在 O(n) 的时间内得到能接的雨水总量. 所以我们可以用动态规划的方法提前得到 每个位置两边的最大高度.
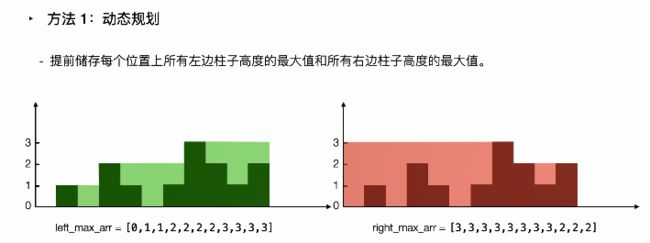
明白动态规划的作用之后, 其实动态规划规划的思想还是挺好理解的, 就是下面的经典的四个步骤. 动态规划最困难的地方在于 推导出递推公式, 但本题的递推公式还是比较容易推导的. 关于动态规划, 是个重中之重, 以后会专门写一个专题详解动态规划的.

一般来说, 动态规划的题目在遍历结束之后就能得到结果了, 但是本题还是需要对动态规划的结果进行进一步的处理才能得到最终的结果.
在得到数组 leftMax 和 rightMax 的每个元素值之后, 对于0≤i 最后总结了四个注意点, 其中三个是Python的语法问题, 和java还是有挺大差别的, 大家注意一下: 上面的动态规划方法虽然将时间复杂度优化到了O(n), 但同时也将空间复杂度由O(1)提升到了O(n), 典型的牺牲空间换取时间的做法, 接下来我们就使用双指针在保证时间复杂度不变的情况下, 将空间复杂度优化到O(1). 我们先来分析两个思想最大的不同之处. 由上面动态规划的图可以看出, 它对于每个位置都找到了两边的最大值, 但实际上, 接的水量是由两者中的较小值决定的, 所以只要找到较少的那个即可, 没必要找到较大的那个的最大值, 这就是我们能够使用双指针进行优化的原因, 可能比较难理解, 大家多思考一下. 同时h[left] < h[right] 的情况只会出现在:right 刚刚找到自己目前的最大值, left在寻找更大值的过程中。 所以此时必然有leftMax < rightMax, 这样就满足了我们寻找两者中较小者的要求. 明白了双指针思想优化的地方之后, 我们再来看双指针的思想就比较容易理解了. 在代码中有个小的注意点就是 左右指针最终并不需要相等, 满足小于的条件就可以了, 因为相等时, 表示它们同时指向最大值, 但是在最高点是不会有雨水的. 这个方法和上面几个就没太大关系了, 但也是一种很重要的算法, 也是有很多的应用场景的, 我们来了解下这个算法的思想. 从名字也可以看出, 它最大的特点就是单调, 也就是栈中的元素要么递增, 要么递降, 如果有新的元素不满足这个特点, 就不断的将栈顶元素出栈, 直到满足为止, 这就是它最重要的思想. 本题设计的是一个单调递减栈: 维护一个单调栈, 单调栈存储的是下标, 满足从栈底到栈顶的下标对应的数组 height 中的元素递减. 我们来分析下单调栈为什么可以满足此题的要求. 首先明确一点: 只有产生凹陷的地方才能存储雨水, 那么高度一定是先减后增, 所以当我们遍历到 增 这个位置的时候, 前面的减的地方(凹陷处)一定会存储雨水, 所以我们就将凹陷处出栈, 来计算它所能存储的雨水量. 用算法思想来表述就是: 从左到右遍历数组, 遍历到下标 i 时, 如果栈内至少有两个元素, 记栈顶元素为top, top 的下面一个元素是 left, 则一定有height[left]≥height[top]。如果height[i]>height[top], 则得到一个可以接雨水的区域. 接下来就是雨水量的计算了, 这里有个很大的区别, 之前的方法都是对于单独的 i 位置进行计算的, 但是单调栈在计算的时候是一个长方形的区域, 是按照长度为1,2,3,4分别来求的, 这是最大的不同点, 理解可能有点困难, 我会在视频中详解的. 该区域的宽度是i−left−1, 高度是min(height[left],height[i])−height[top], 根据宽度和高度即可计算得到该区域能接的雨水量. 在代码中有两个要注意的点: 一个是 弹出栈顶后判断栈是否为空, 因为当栈为空, 说明左边不存在最大值, 是无法接雨水的. 另一点就是在Python中一般都是利用列表来实现栈的, 并没有使用单独的数据结构, 所以在操作上和真正的栈是有点不同的, 具体操作如下: 我的更多精彩文章链接, 欢迎查看 各种电脑/软件/生活/音乐/动漫/电影技巧汇总(你肯定能够找到你需要的使用技巧) 力扣算法刷题 根据思维导图整理笔记快速记忆算法重点内容(欢迎和博主一起打卡刷题哦) 计算机专业知识 思维导图整理 最值得收藏的 Python 全部知识点思维导图整理, 附带常用代码/方法/库/数据结构/常见错误/经典思想(持续更新中) 最值得收藏的 C++ 全部知识点思维导图整理(清华大学郑莉版), 东南大学软件工程初试906科目 最值得收藏的 计算机网络 全部知识点思维导图整理(王道考研), 附带经典5层结构中英对照和框架简介 最值得收藏的 算法分析与设计 全部知识点思维导图整理(北大慕课课程) 最值得收藏的 数据结构 全部知识点思维导图整理(王道考研), 附带经典题型整理 最值得收藏的 人工智能导论 全部知识点思维导图整理(王万良慕课课程) 最值得收藏的 数值分析 全部知识点思维导图整理(东北大学慕课课程) 最值得收藏的 数字图像处理 全部知识点思维导图整理(武汉大学慕课课程) 红黑树 一张导图解决红黑树全部插入和删除问题 包含详细操作原理 情况对比 各种常见排序算法的时间/空间复杂度 是否稳定 算法选取的情况 改进 思维导图整理 人工智能课件 算法分析课件 Python课件 数值分析课件 机器学习课件 图像处理课件 考研相关科目 知识点 思维导图整理 考研经验–东南大学软件学院软件工程(这些基础课和专业课的各种坑和复习技巧你应该知道) 东南大学 软件工程 906 数据结构 C++ 历年真题 思维导图整理 东南大学 软件工程 复试3门科目历年真题 思维导图整理 最值得收藏的 考研高等数学 全部知识点思维导图整理(张宇, 汤家凤), 附做题技巧/易错点/知识点整理 最值得收藏的 考研线性代数 全部知识点思维导图整理(张宇, 汤家凤), 附带惯用思维/做题技巧/易错点整理 高等数学 中值定理 一张思维导图解决中值定理所有题型 考研思修 知识点 做题技巧 同类比较 重要会议 1800易错题 思维导图整理 考研近代史 知识点 做题技巧 同类比较 重要会议 1800易错题 思维导图整理 考研马原 知识点 做题技巧 同类比较 重要会议 1800易错题 思维导图整理 考研数学课程笔记 考研英语课程笔记 考研英语单词词根词缀记忆 考研政治课程笔记 Python相关技术 知识点 思维导图整理 Numpy常见用法全部OneNote笔记 全部笔记思维导图整理 Pandas常见用法全部OneNote笔记 全部笔记思维导图整理 Matplotlib常见用法全部OneNote笔记 全部笔记思维导图整理 PyTorch常见用法全部OneNote笔记 全部笔记思维导图整理 Scikit-Learn常见用法全部OneNote笔记 全部笔记思维导图整理 Java相关技术/ssm框架全部笔记 Spring springmvc Mybatis jsp 科技相关 小米手机 小米 红米 历代手机型号大全 发布时间 发布价格 常见手机品牌的各种系列划分及其特点 历代CPU和GPU的性能情况和常见后缀的含义 思维导图整理

3.双指针 优化空间复杂度

4.单调栈的思想

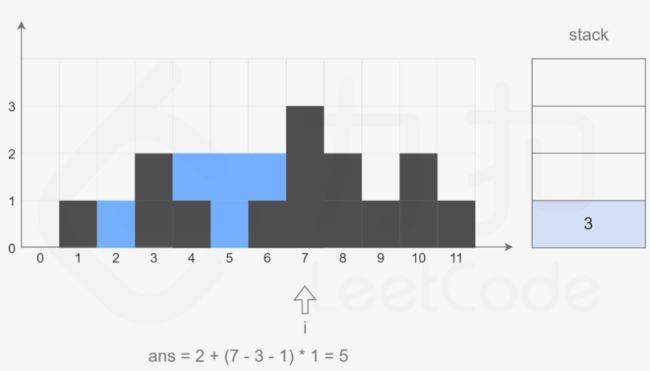
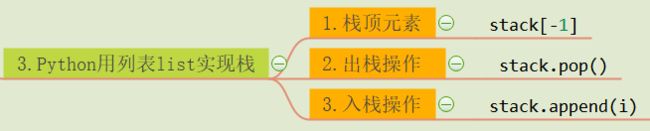
源码
Python:
# 动态规划
class Solution:
def trap(self, height: List[int]) -> int:
if not height:
return 0
n = len(height)
leftMax = [height[0]] + [0] * (n - 1) # 简化的连续赋值
# 正向遍历数组 height 得到数组 leftMax 的每个元素值
for i in range(1, n):
leftMax[i] = max(leftMax[i - 1], height[i])
# 反向遍历数组 height 得到数组 rightMax 的每个元素值
rightMax = [0] * (n - 1) + [height[n - 1]]
for i in range(n - 2, -1, -1): # 逆序遍历
rightMax[i] = max(rightMax[i + 1], height[i])
# 遍历每个下标位置即可得到能接的雨水总量
ans = sum(min(leftMax[i], rightMax[i]) - height[i] for i in range(n))
return ans
# 双指针
class Solution:
def trap(self, height: List[int]) -> int:
ans = 0
left, right = 0, len(height) - 1
leftMax = rightMax = 0
# 不需要相等,相等时,同时指向最大值,在最高点不会有雨水的
while left < right:
leftMax = max(leftMax, height[left])
rightMax = max(rightMax, height[right])
if height[left] < height[right]:
ans += leftMax - height[left]
left += 1
else:
ans += rightMax - height[right]
right -= 1
return ans
# 单调栈
class Solution:
def trap(self, height: List[int]) -> int:
ans = 0
stack = list() # 用列表来模拟实现栈
n = len(height)
for i, h in enumerate(height): # 同时获取下标和对应的高度
# height[i] > height[stack[-1]]得到一个可以接雨水的区域
while stack and h > height[stack[-1]]:
top = stack.pop()
if not stack: # 栈为空,左边不存在最大值,无法接雨水
break
left = stack[-1] # left成为新的栈顶元素
currWidth = i - left - 1 # 获取接雨水区域的宽度
currHeight = min(height[left], height[i]) - height[top]
ans += currWidth * currHeight
stack.append(i) # 在对下标i处计算能接的雨水量之后,将i入栈,继续遍历后面的下标
return ans
java:
# 常规思想
class Solution {
public int trap(int[] height) {
int ans = 0;
int size = height.length;
for (int i = 1; i < size - 1; i++) {
int max_left = 0, max_right = 0;
for (int j = i; j >= 0; j--) {
// 向左扫描记录左边最大值
max_left = Math.max(max_left, height[j]);
}
for (int j = i; j < size; j++) {
// 向右扫描记录右边最大值
max_right = Math.max(max_right, height[j]);
} // 下标i处能接到的水量
ans += Math.min(max_left, max_right) - height[i];
}
return ans;
}
}
# 动态规划
class Solution {
public int trap(int[] height) {
int n = height.length;
if (n == 0) {
return 0;
}
// 正向遍历数组 height 得到数组 leftMax 的每个元素值
int[] leftMax = new int[n];
leftMax[0] = height[0];
for (int i = 1; i < n; ++i) {
leftMax[i] = Math.max(leftMax[i - 1], height[i]);
}
// 反向遍历数组 height 得到数组 rightMax 的每个元素值
int[] rightMax = new int[n];
rightMax[n - 1] = height[n - 1];
for (int i = n - 2; i >= 0; --i) {
rightMax[i] = Math.max(rightMax[i + 1], height[i]);
}
// 遍历每个下标位置即可得到能接的雨水总量
int ans = 0;
for (int i = 0; i < n; ++i) {
ans += Math.min(leftMax[i], rightMax[i]) - height[i];
}
return ans;
}
}
# 双指针
class Solution {
public int trap(int[] height) {
int ans = 0;
int left = 0, right = height.length - 1;
int leftMax = 0, rightMax = 0;
// 不需要相等,相等时,同时指向最大值,在最高点不会有雨水的
while (left < right) {
leftMax = Math.max(leftMax, height[left]);
rightMax = Math.max(rightMax, height[right]);
if (height[left] < height[right]) {
ans += leftMax - height[left];
++left;
} else {
ans += rightMax - height[right];
--right;
}
}
return ans;
}
}
# 单调栈
class Solution {
public int trap(int[] height) {
int ans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
int n = height.length;
for (int i = 0; i < n; ++i) {
// height[i] > height[stack.peek()]得到一个可以接雨水的区域
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop(); // 获得接雨水位置的下标
if (stack.isEmpty()) {
// 栈为空,左边不存在最大值,无法接雨水
break;
}
int left = stack.peek(); // left成为新的栈顶元素
int currWidth = i - left - 1; // 获取接雨水区域的宽度
int currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i); // 在对下标i处计算能接的雨水量之后,将i入栈,继续遍历后面的下标
}
return ans;
}
}
![]()
