2021年暑假ACM集训队模拟赛第4场——题解
目录
- A 山峦叠嶂
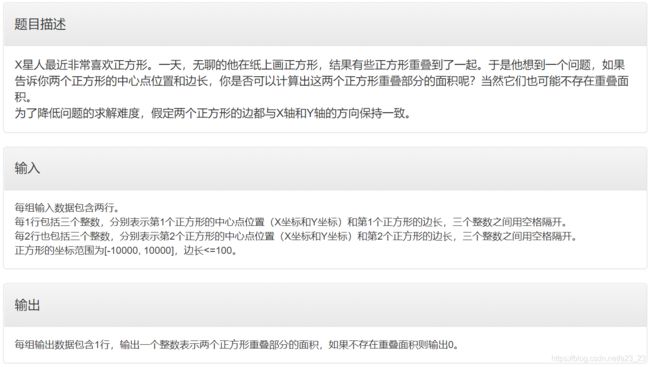
- B 重叠正方形
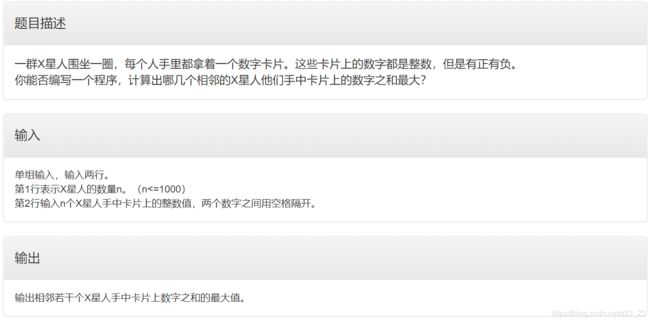
- C 一群X星人
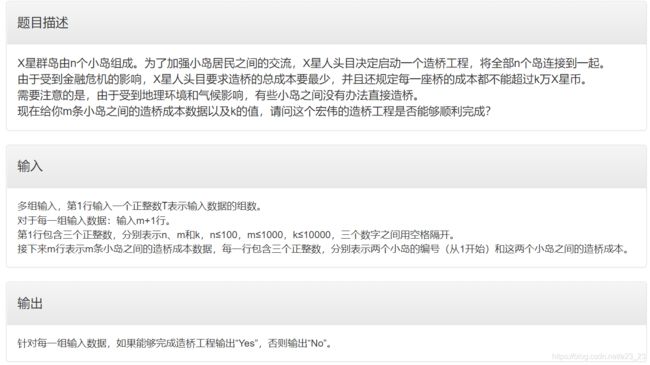
- D X星群岛 (MST,最小生成树模板题)
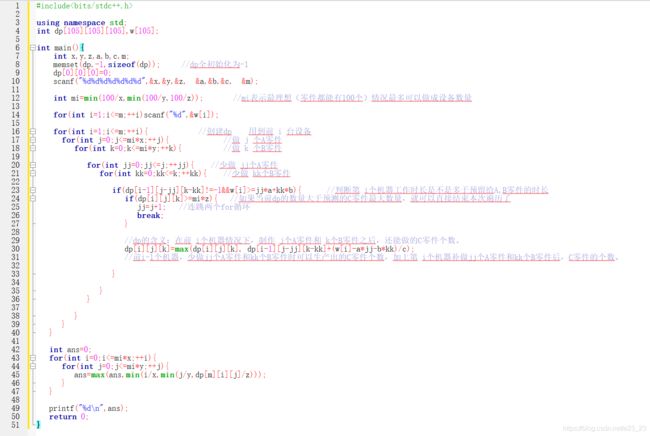
- E X星人的飞行设备(复杂一点的DP)
- F X星人的救援
- G 最长回文子串
- H DNA序列拼接
- I 防水板砖(搜索,DFS)
- J 黑白树(比较复杂一点的数据结构题,Tree 待补)
A 山峦叠嶂
样例输入 Copy
5
1265 2368 3474 2170 3982
样例输出 Copy
1
代码:
#include
//break;
}
}
}
cout<<n-ma<<endl;
return 0;
}
B 重叠正方形
样例输入 Copy
0 0 2
1 1 2
样例输出 Copy
1
代码:
#include
if(num<=0) num=0;
num*=min((r1+r2)/2.0-(double)fabs(y1-y2),mi);
//cout<<"y="<
if(num<=0) num=0;
double nu=(double)min(r1,r2);
num=min(nu*nu,num);
printf("%.0lf\n",num);
}
return 0;
}
C 一群X星人
样例输入 Copy
5
10 -5 8 -4 2
样例输出 Copy
16
代码:
#include
}
//cout<
num+=a[i];
}
for(int i=1;i<=n;i++){
for(int j=1;j<i;j++){
ma=max(dp[i][n]+dp[1][j],ma);
}
}
cout<<ma<<endl;
return 0;
}
D X星群岛 (MST,最小生成树模板题)
样例输入 Copy
2
3 3 400
1 2 200
1 3 300
2 3 500
3 3 400
1 2 500
1 3 600
2 3 700
样例输出 Copy
Yes
No
我这道题一直Wa,补题的时候才发现,m条路径,我居然用的n遍历的。。。哭了。。。
代码:
#include
cout<<"Yes"<<endl;
else
cout<<"No"<<endl;
}
return 0;
}
E X星人的飞行设备(复杂一点的DP)
样例输入 Copy
1 1 1
100 200 300
2
2000 3000
样例输出 Copy
8
思路:
看了大佬的代码,我觉得题意是:每条生产线可以制作A,B,C的零件,但是能制作多少是不确定的,我们得合理利用生产线时长,达到组合的设备数目最多的目的,当然其中每条生产线可能最后会浪费一些时间(剩余时间不足以生产任意一种零件的情况)
代码:
#includeF X星人的救援
样例输入 Copy
2
3 33 450
5 7 8
1 2 4
4 5 7
3 50 3
0 60 -1
60 0 100
-1 100 0
样例输出 Copy
Yes
No
代码:
#includeG 最长回文子串
样例输入 Copy
DABBACD
样例输出 Copy
6
代码:
#includeH DNA序列拼接
样例输入 Copy
4
AGCT
GCTAA
TAACG
CTAACGGCG
样例输出 Copy
11
提示
在样例中,“AGCT”和“GCTAA”可拼接为“AGCTAA”;“AGCTAA”和“CTAACGGCG”可拼接为“AGCTAACGGCG”,长度为11。
代码:
#include
continue;
}
int nu=3;
//cout<
if(a[j].find(b)<a[j].size()){
int le=a[j].find(b),k=2;
//cout<<"le="<
for(k=k+1;k+le<a[j].size()&&k<a[i].size();k++){
if(a[j][le+k]!=a[i][k]) break;
}
//cout<
if(k+le==a[j].size()){
dp[i][j]=k;
//cout<<" k="<
}
}
//cout<
}
//cout<
}
mi=0;
for(int i=0;i<n;i++){
m[i]=1;
bfs(i,a[i].size());
m[i]=0;
}
cout<<mi<<endl;
return 0;
}
I 防水板砖(搜索,DFS)
样例输入 Copy
4 4
2 3 5 1
4 1 2 3
1 5 4 2
1 2 2 2
样例输出 Copy
1
思路:
这一题我觉得最难的是读懂题意,虽然我说服了自己这个题的意思是这个,但是感觉还可以理解成其他意思
题目的意思就是找到有多少个水坑,但在寻找过程中,相邻(上下/左右相邻)的小水坑才能合并。这道题的思路就是先找到第一个小水坑,条件是上下左右的数量都大于它。再根据找到的小水坑去找可以合并的其他小水坑,这个时候其他小水坑的条件就是上下左右的数量有三边是大于它就可以了(因为第一个找到的小水坑是相邻并且小于第二个的),依次类推dfs
这个时候就发现有个测试数据是这样的:
4 5
0 5 6 5 0
5 2 2 3 5
5 2 2 4 5
0 6 6 5 0
输出是:0
是的,这个代码判断(2,2)(2,2)是不算水坑的。。我也不知道题目要求是算还是不算
但题目过了呀!那就不深究了
代码:
#includeJ 黑白树(比较复杂一点的数据结构题,Tree 待补)
样例输入 Copy
7
1 2 0
3 1 1
2 4 0
5 2 0
6 3 1
5 7 1
样例输出 Copy
1