【计量经济学导论】05. 异方差

异方差

在上一节的讨论中，完全共线性问题违背了基本假定 MLR.3 ，而多重共线性没有违背任何一个基本假定，因此 OLS 估计量仍然具有 BLUE 性质。这一篇笔记我们主要来讨论异方差问题，即如果违背了同方差假定 MLR.5 的情况。

异方差的含义

在介绍异方差之前，我们先回顾一下同方差的情况。方差是度量被解释变量的观测值围绕回归线的分散程度，因此同方差假定指的是所有观测值的分散程度相同。
$$\mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{u}|\mathbf{X})=\left[\begin{array}{cccc}{\sigma }^2& & & \\ & {\sigma }^2& & \\ & & \ddots & \\ & & & {\sigma }^2\end{array}\right]={\sigma }^2\left[\begin{array}{cccc}1& & & \\ & 1& & \\ & & \ddots & \\ & & & 1\end{array}\right]={\sigma }^2{\mathbf{I}}_n.$$
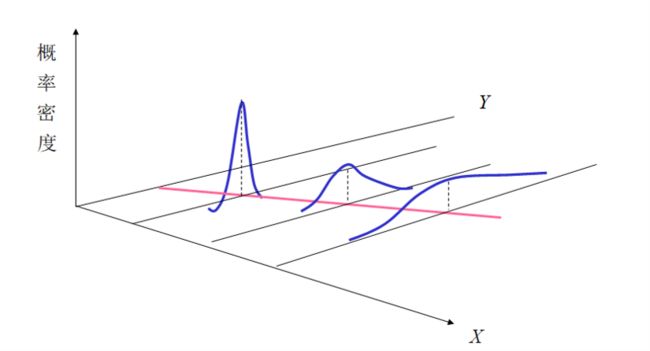
异方差指的是对于不同的样本点，随机干扰项的方差不再是常数，而是互不相同的。即如果 $u$ 的方差随 $x$ 变化，那么称随机干扰项是具有异方差的。当异方差发生的时候，随机干扰项的条件方差是关于解释变量的函数：
$$\mathrm{V}\mathrm{a}\mathrm{r}(u|X_1,X_2,...,X_k)=g(X_1,X_2,...X_k).$$
用协方差矩阵表示为：
$$\mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{u}|\mathbf{X})=\left[\begin{array}{cccc}{\sigma }_1^2& & & \\ & {\sigma }_2^2& & \\ & & \ddots & \\ & & & {\sigma }_n^2\end{array}\right]={\sigma }^2\left[\begin{array}{cccc}{\omega }_1& & & \\ & {\omega }_2& & \\ & & \ddots & \\ & & & {\omega }_n\end{array}\right]={\sigma }^2\mathbf{\Omega }.$$

这里的 $\mathrm{V}\mathrm{a}\mathrm{r}(u_i)={\sigma }_i^2$ ，下标 $i$ 表示非常数，违背了 MLR.5。

用图形表示为：

异方差的产生原因

(1) 模型中遗漏了某些重要的解释变量

举个例子比较容易理解。假设正确的计量模型是：
$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+u_i,$$
如果我们遗漏了解释变量 $X_{i2}$ ，估计的模型为：
$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+v_i,$$
当被遗漏的 $X_{2i}$ 与 $X_{i1}$ 具有呈现同方向或反方向的变化趋势时， $X_{2i}$ 随 $X_{i1}$ 的有规律的变化会体现在随机干扰项 $v_i$ 中。一般这种情况往往也会造成内生性的问题，我们在后面的章节进行介绍。

(2) 数据的测量误差

样本数据的观测误差有可能随研究范围的扩大而增加，或随时间的推移逐步积累，也可能随着观测技术的提高而逐步减小。

(3) 截面数据中总体各单位的差异

通常认为，截面数据较时间序列数据更容易产生异方差。这是因为同一时点不同对象的差异，一般说来会大于同一对象不同时间的差异。不过，在时间序列数据发生较大变化的情况下，也可能出现比截面数据更严重的异方差。

(4) 一个或多个回归解释变量的分布是偏态（skewness）

例如：收入、财富和受教育水平的总体分布都是不均匀的分布。具体体现在大部分的收入和财富被少数人所拥有，受高等教育的精英也是少数等等。

(5) 模型的函数形式存在设定误差

(6) 异常值

异方差的后果

• 不改变无偏性和一致性：参数估计的无偏性仅依赖于基本假定中的零均值假定，所以异方差的存在对无偏性的成立没有影响。

• 参数估计量非有效：同方差假定是 OLS 估计方差最小的前提条件，所以随机误差项是异方差时，将不能再保证最小二乘估计的方差最小。我们重新写一遍矩阵形式的推导过程就可以清楚的发现问题：

$$\begin{array}{rl}\mathrm{V}\mathrm{a}\mathrm{r}(\hat{\mathbf{\beta }}|\mathbf{X})& =\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathbf{\beta }+{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{\mu }\right)\\ & ={\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\cdot \mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{\mu }|\mathbf{X})\cdot \mathbf{X}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}\\ & ={\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\cdot {\sigma }^2\mathbf{\Omega }\cdot \mathbf{X}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}\\ & ={\sigma }^2{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\mathrm{T}}\cdot \mathbf{\Omega }\cdot \mathbf{X}{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}\\ & \ne {\sigma }^2{\left({\mathbf{X}}^{\mathrm{T}}\mathbf{X}\right)}^{-1}.\end{array}$$

• $\mathrm{V}\mathrm{a}\mathrm{r}(\widehat{{\beta }_j})$ 非有效会造成一系列的影响：
  • 不能用来构造置信区间和 $t$ 统计量，使用大样本容量也不能解决这个问题；
  • 变量的显著性检验失去意义；
  • 模型的预测失效。

在这里我们利用排除其他解释变量影响的方法简单回顾一下同方差条件下的 $t$ 统计量：
$$t=\frac{{\hat{\beta }}_j-{\beta }_j}{\mathrm{s}\mathrm{e}({\hat{\beta }}_j)}=\frac{{\hat{\beta }}_j-{\beta }_j}{\sqrt{\frac{{\hat{\sigma }}^2}{{\mathrm{S}\mathrm{S}\mathrm{T}}_j(1-R_j^2)}}}=\frac{{\hat{\beta }}_j-{\beta }_j}{\sqrt{\frac{{\hat{\sigma }}^2\cdot {\sigma }^2}{{\mathrm{S}\mathrm{S}\mathrm{T}}_j(1-R_j^2)\cdot {\sigma }^2}}}=\frac{\frac{{\hat{\beta }}_j-{\beta }_j}{\mathrm{s}\mathrm{d}({\hat{\beta }}_j)}}{\sqrt{\frac{{\hat{\sigma }}^2}{{\sigma }^2}}},$$

其中分子服从标准正态分布，分母的平方乘以 $n-k-1$ 服从自由度为 $n-k-1$ 的 ${\chi }^2$ 分布。

关于异方差下的 OLS 估计量的方差，我们也利用排除其他解释变量影响的方法，通过如下推导可以发现问题：
$$\mathrm{V}\mathrm{a}\mathrm{r}({\hat{\beta }}_j|\mathbf{X})=\mathrm{V}\mathrm{a}\mathrm{r}\left({\beta }_j+\frac{\sum _{i=1}^n{\hat{r}}_{ij}{u}_i}{\sum _{i=1}^n{\hat{r}}_{ij}^2}|\mathbf{X}\right)=\frac{\sum _{i=1}^n{\hat{r}}_{ij}^2\cdot \mathrm{V}\mathrm{a}\mathrm{r}\left(u_i|\mathbf{X}\right)}{{\left(\sum _{i=1}^n{\hat{r}}_{ij}^2\right)}^2}$$

由于违背了同方差假设， $\mathrm{V}\mathrm{a}\mathrm{r}\left({\hat{\beta }}_i|\mathbf{X}\right)$ 是一个很复杂的形式，无法得到准确的 OLS 估计量的方差。在这种情况下，原本用来计算 $t$ 统计量的分子也不再服从标准正态分布，使得 $t$ 检验失效。

异方差的检验方法

一般地，通过数理统计的方法检验异方差性，基本思路都是设原假设为不存在异方差性：
$$H_0:\mathrm{E}(u^2|x_1,x_2,...,x_k)={\sigma }^2.$$
这一点很容易理解，当我们构造检验统计量时，同方差原假设下的检验统计量往往具有良好的统计分布，便于进行假设检验。下面我们提出几种检验异方差的方法。

图示检验法

• 做 $Y$ 对 $X$ 的散点图：方差描述的是随机变量的取值相对于其均值的离散程度。因为被解释变量 $Y$ 与随机误差项 $u$ 有相同的方差，所以利用分析 $Y$ 与 $X$ 的相关图形，可以初略地看到 $Y$ 的离散程度与 $X$ 之间是否有相关关系。如果随着 $X$ 的增加，$Y$ 的离散程度为逐渐增大（或减小）的变化趋势，则认为存在递增型（或递减型）的异方差现象。
• 做残差 $e_i^2$ 对 $X$ 的散点图：适用于一元回归模型，
  • 如果 $e_i^2$ 的离散程度不随 $X_i$ 变化，则表明不存在异方差；
  • 如果 $e_i^2$ 的离散程度随 $X_i$ 变化，则表明存在异方差。

Breusch-Pagan 检验

B-P 检验是一种较为常见的异方差的检验方法。检验是否存在异方差，即检验随机误差项的方差是否与模型的解释变量相关。比较常见的就是和解释变量的一次项具有某种线性关系。

假设需要检验的模型为：
$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+\cdots +{\beta }_k{X}_{ik}+u_i,$$
B-P 检验的步骤如下：

将 $Y$ 对 $X_1,X_2,\cdots ,X_k$ 回归，得到估计值并计算拟合值 $\hat{Y}$ 和残差 $e_i$ ：
$${\hat{Y}}_i={\hat{\beta }}_0+{\hat{\beta }}_1{X}_{i1}+{\hat{\beta }}_2{X}_{i2}+\cdots +{\hat{\beta }}_k{X}_{ik},$$

$$e_i=Y_i-{\hat{Y}}_i.$$

将 OLS 估计后的 $e_i^2$ 对解释变量的一次项做辅助回归，得到估计值和可决系数 $R_{e^2}^2$ 。
$$e_i^2={\delta }_0+{\delta }_1{X}_{i1}+{\delta }_2{X}_{i2}+...+{\delta }_k{X}_{ik}+{\epsilon }_i,$$

检验联合假设 $H_0:{\delta }_1={\delta }_2=...={\delta }_k=0$ ，可通过在约束条件下的受约束回归检验或拉格朗日乘数检验进行：

计算 $F$ 统计量，检验 $p$ 值：
$$F=\frac{R_{e^2}^2/k}{(1-R_{e^2}^2)/(n-k-1)}\sim F(k,n-k-1),$$

计算 $LM$ 统计量，检验 $p$ 值：
$$LM=n\cdot R_{e^2}^2\sim {\chi }^2(k).$$

White 检验

White 检验可以看成 B-P 检验的一种拓展，不需要关于异方差的任何先验信息，只需要在大样本的情况下，将 OLS 估计后的残差平方 $e_i^2$ 对常数、解释变量、解释变量的平方项及其交叉项等所构成一个辅助回归，利用辅助回归建立相应的检验统计量来判断异方差性。 不仅能够检验异方差的存在性，同时在多变量的情况下，还能判断出是哪一个变量的何种函数形式引起的异方差。

我们以三元回归模型为例，设需要检验的模型为：
$$Y_i={\beta }_0+{\beta }_1{X}_{i1}+{\beta }_2{X}_{i2}+{\beta }_3{X}_{i3}+u_i,$$
将 $Y$ 对 $X_1,X_2,X_3$ 回归，得到估计值并计算拟合值 $\hat{Y}$ 和残差 $e_i$ 后，建立辅助回归模型：
$$\begin{array}{rl}{e}^2=& {\delta }_0+{\delta }_1{X}_1+{\delta }_2{X}_2+{\delta }_3{X}_3\\ & +{\delta }_4{X}_1^2+{\delta }_5{X}_2^2+{\delta }_6{X}_3^2\\ & +{\delta }_7{X}_1{X}_2+{\delta }_8{X}_1{X}_3+{\delta }_9{X}_2{X}_3+{\epsilon }_i.\end{array}$$

检验联合假设 $H_0:{\delta }_1={\delta }_2=...={\delta }_9=0$ ，

计算 $F$ 统计量，检验 $p$ 值：
$$F=\frac{R_{e^2}^2/h}{(1-R_{e^2}^2)/(n-h-1)}\sim F(h,n-h-1),$$
计算 $LM$ 统计量，检验 $p$ 值：
$$LM=n\cdot R_{e^2}^2\sim {\chi }^2(h)$$

其中 $n$ 为样本容量，$h$ 为辅助回归的解释变量个数（在三元回归模型中，$h=9$）。

简化的 White 检验

我们在做 White 检验的时候需要跑一个很长的回归，且随着解释变量的增多，自由度的损失严重，因此 While 检验可以做以下简化：
$$e_i^2={\delta }_0+{\delta }_1{\hat{Y}}_i+{\delta }_2{\hat{Y}}_i^2+{\epsilon }_i$$

将用拟合值及其多项式代替所有的解释变量，并检验联合假设 $H_0:{\delta }_1={\delta }_2=0$ ，同理可用 $F$ 统计量和 $LM$ 统计量进行假设检验。这样可以大大减少辅助回归的长度和自由度的损失。

Park 检验和 Glejser 检验

这两种检验的方式类似：由 OLS 法得到残差，分别取平方、绝对值以及绝对值的对数，然后将这些新的变量分别对某些解释变量回归，根据回归模型的显著性和拟合优度来判断是否存在异方差。

不仅能对异方差的存在进行判断，而且还能对异方差随某个解释变量变化的函数形式进行诊断。一旦发现异方差，即知道其形式。但缺点是计算量较大，且该检验要求变量的观测值为大样本。

Park 检验：
$$e_i^2=f(X_{ij})+{\epsilon }_i$$

Glejser 检验：
$$|e_i|=f(X_{ij})+{\epsilon }_i$$

$$\ln |e_i|=f(X_{ij})+{\epsilon }_i$$

这里的 $e_i$ 仍然是原始回归模型的残差，函数 $f(\cdot )$ 是部分解释变量 $X$ 的某种最佳函数形式。检验方式仍然是 $F$ 检验和 $LM$ 检验。

Goldfeld-Quanadt 检验

该检验的基本思想为：将样本分为两部分，然后分别对两个样本进行回归，并计算两个子样的残差平方和所构成的比值，以此为统计量来判断是否存在异方差。但这一检验需要满足两个前提条件：

• 要求变量的观测值为大样本；
• 除了同方差假定不成立外，其它假定均满足。

检验的具体做法如下：

1. 排序：假设随机扰动项的方差与某个解释变量正相关，把全部观测值按照此解释变量的取值从小到大排序。
2. 数据分组：将排列在中间的约 $1/4$ 的观察值删除掉，记为 $c$ ，再将剩余的分为两个部分，每部分观察值的个数为 $(n-c)/2$ 。
3. 分别 OLS 回归：用两个子样本分别估计回归直线，并计算残差平方和。分别用 $n_2$ 和 $n_1$ 表示两组样本，用 ${\mathrm{S}\mathrm{S}\mathrm{R}}_2=\sum _{i=1}^{n_2}{e}_{2i}^2$ 和 ${\mathrm{S}\mathrm{S}\mathrm{R}}_1=\sum _{i=1}^{n_1}{e}_{1i}^2$ 表示两组样本的残差平方和。这里的 $n_2=n_1=(n-c)/2$ 。
4. 构造 $F$ 统计量：在同方差假设下，两组样本方差应该相等，因此提出原假设 $H_0:{\sigma }_1^2={\sigma }_2^2$ ，并进行 $F$ 检验：

$$F=\frac{{\mathrm{S}\mathrm{S}\mathrm{R}}_2/(n_2-k-1)}{{\mathrm{S}\mathrm{S}\mathrm{R}}_1/(n_1-k-1)}=\frac{{\mathrm{S}\mathrm{S}\mathrm{R}}_2}{{\mathrm{S}\mathrm{S}\mathrm{R}}_1}\sim F(n_2-k-1,n_1-k-1).$$

该检验的缺点在于检验结果与选择数据删除的个数 $c$ 的大小有关，且只能判断异方差是否存在。

异方差的修正措施

异方差稳健的标准误法

这里是我们第一次提出稳健的标准误的概念，事实上稳健的标准误有很多种，这里指的是 White 提出的针对异方差的情况采用的稳健的标准误。主要思想是：仍采用 OLS 估计量，但修正其方差。

原理是当我们修正了 OLS 估计量的方差时，在大样本条件下有：
$$t=\frac{{\hat{\beta }}_j-{\beta }_j}{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{t}\_\mathrm{s}\mathrm{e}({\hat{\beta }}_j)}\stackrel{a}{\sim }N(0,1),$$
这里 $\stackrel{a}{\sim }$ 表示渐进服从，此时我们可以构造出合理的 $t$ 统计量。这里说明一下，$t$ 分布在自由度很大的时候可以近似看作标准正态分布。

那么如何来构造稳健的标准误呢？White 提出用 OLS 估计的残差的平方 $e_i^2$ 作为相应 ${\sigma }_i^2$ 的代表。具体操作如下：

在计算一元回归模型的时候，${\hat{\beta }}_1$ 的方差可以有如下的计算公式：
$$\mathrm{V}\mathrm{a}\mathrm{r}({\hat{\beta }}_1)=\frac{\sum _{i=1}^n{\left(X_i-\bar{X}\right)}^2{\sigma }_i^2}{{\left(\sum _{i=1}^n{\left(X_i-\bar{X}\right)}^2\right)}^2}.$$
在同方差假定下，${\sigma }_i^2={\sigma }^2$ ，我们可以用 ${\hat{\sigma }}^2$ 代替 ${\sigma }^2$ 计算标准误。当出现异方差的情况下，我们用用 $e_i^2$ 作为 ${\sigma }_i^2$ 的估计计算的到稳健的方差：
$$\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{u}\mathrm{s}\mathrm{t}\_\mathrm{V}\mathrm{a}\mathrm{r}({\hat{\beta }}_1)=\frac{\sum _{i=1}^n{\left(X_i-\bar{X}\right)}^2{e}_i^2}{{\left(\sum _{i=1}^n{\left(X_i-\bar{X}\right)}^2\right)}^2}.$$
进而开方得到即可得到稳健的标准误。多元回归模型中，我们可以使用排除其他变量影响的方法计算 OLS 估计量的方差，利用同样的处理方式也可以得到稳健的标准误。

一般地，在小样本下需要检验是否存在异方差性，在大样本下直接汇报稳健的标准误。

加权最小二乘法 WLS / 广义最小二乘法 GLS

笔记的开篇我们假设了出现异方差情况时，随机干扰项的方差-协方差矩阵的结构：
$$\mathrm{V}\mathrm{a}\mathrm{r}(\mathbf{u}|\mathbf{X})={\sigma }^2\left[\begin{array}{cccc}{\omega }_1& & & \\ & {\omega }_2& & \\ & & \ddots & \\ & & & {\omega }_n\end{array}\right]={\sigma }^2\mathbf{\Omega }.$$
若 $\mathbf{\Omega }$ 已知，我们可以对原模型进行变换，使之变成一个新的不存在异方差的模型，然后采用 OLS 估计其参数，变化过程如下：
$$\mathbf{W}={\mathbf{\Omega }}^{-1}=\left[\begin{array}{cccc}\frac{1}{{\omega }_1}& & & \\ & \frac{1}{{\omega }_2}& & \\ & & \ddots & \\ & & & \frac{1}{{\omega }_n}\end{array}\right]={\left[\begin{array}{cccc}\frac{1}{\sqrt{{\omega }_1}}& & & \\ & \frac{1}{\sqrt{{\omega }_2}}& & \\ & & \ddots & \\ & & & \frac{1}{\sqrt{{\omega }_n}}\end{array}\right]}^2={\mathbf{P}}^{\mathrm{T}}\mathbf{P},$$
其中 $\mathbf{W}$ 是 $\mathbf{\Omega }$ 的逆矩阵，是一个对称正定矩阵，因此存在一可逆矩阵 $\mathbf{P}$ 使得 $\mathbf{W}={\mathbf{P}}^{\mathrm{T}}\mathbf{P}$。利用该可逆矩阵 $\mathbf{P}$ 将模型变换为：
$$\mathbf{P}\mathbf{Y}=\mathbf{P}\mathbf{X}\mathbf{\beta }+\mathbf{P}\mathbf{\mu }⟶{\mathbf{Y}}^{\ast }={\mathbf{X}}^{\ast }\mathbf{\beta }+{\mathbf{\mu }}^{\ast }$$
用 OLS 估计新模型
$$\tilde{\mathbf{\beta }}=({{\mathbf{X}}^{\ast }}^{\mathrm{T}}{\mathbf{X}}^{\ast }{)}^{-1}{{\mathbf{X}}^{\ast }}^{\mathrm{T}}{\mathbf{Y}}^{\ast }=({\mathbf{X}}^{\mathrm{T}}{\mathbf{P}}^{\mathrm{T}}\mathbf{P}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{T}}{\mathbf{P}}^{\mathrm{T}}\mathbf{P}\mathbf{Y}=({\mathbf{X}}^{\mathrm{T}}\mathbf{W}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathrm{T}}\mathbf{W}\mathbf{Y}.$$
这就是原模型的 WLS 估计量， 是无偏且有效的估计量。

可行的广义最小二乘法 FGLS

若 $\mathbf{\Omega }$ 未知，需要先估计 ${\sigma }_i^2$ ，然后利用 ${\sigma }_i^2$ 的估计值 ${\hat{\sigma }}_i^2$ 建立加权的新模型，再用 OLS 估计新模型。假设部分解释变量造成异方差，记为 $Z_1,Z_2,\cdots ,Z_p$ ，我们一般设定如下可能的计量模型：

$${\sigma }_i^2={\alpha }_0+{\alpha }_1{Z}_{i1}+{\alpha }_2{Z}_{i2}+...+{\alpha }_p{Z}_{ip}+{\nu }_i,$$

$${\sigma }_i={\alpha }_0+{\alpha }_1{Z}_{i1}+{\alpha }_2{Z}_{i2}+...+{\alpha }_p{Z}_{ip}+{\nu }_i,$$

$$\ln {\sigma }_i^2={\alpha }_0+{\alpha }_1{Z}_{i1}+{\alpha }_2{Z}_{i2}+...+{\alpha }_p{Z}_{ip}+{\nu }_i,（常见）$$

用回归的残差 $e_i$ 代替 ${\sigma }_i$ 进行上述 OLS 估计，获得估计残参数并计算出拟合值，将 $e_i^2$ 的拟合值 ${\hat{e}}_i^2$ 作为 ${\sigma }_i^2$ 的估计值 ${\hat{\sigma }}_i^2$ ：
$${\hat{\sigma }}_i^2={\hat{\alpha }}_0+{\hat{\alpha }}_1{Z}_{i1}+{\hat{\alpha }}_2{Z}_{i2}+...+{\hat{\alpha }}_p{Z}_{ip},$$

$${\hat{\sigma }}_i^2={\left({\hat{\alpha }}_0+{\hat{\alpha }}_1{Z}_{i1}+{\hat{\alpha }}_2{Z}_{i2}+...+{\hat{\alpha }}_p{Z}_{ip}\right)}^2,$$

$${\hat{\sigma }}_i^2=\exp \left({\hat{\alpha }}_0+{\hat{\alpha }}_1{Z}_{i1}+{\hat{\alpha }}_2{Z}_{i2}+...+{\hat{\alpha }}_p{Z}_{ip}\right),$$

之后便可以利用 WLS 估计原模型的系数：
$$\frac{Y_i}{{\hat{\sigma }}_i}={\beta }_0\frac{1}{{\hat{\sigma }}_i}+{\beta }_1\frac{X_{i1}}{{\hat{\sigma }}_i}+{\beta }_2\frac{X_{i2}}{{\hat{\sigma }}_i}+...+{\beta }_k\frac{X_{ik}}{{\hat{\sigma }}_i}+u_i.$$