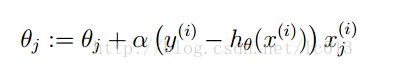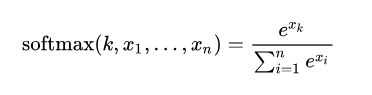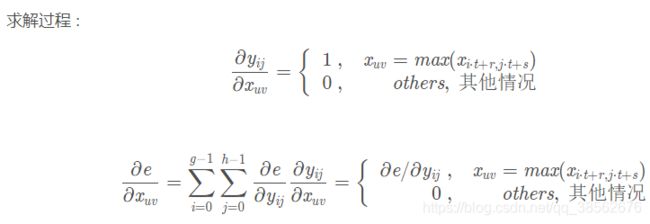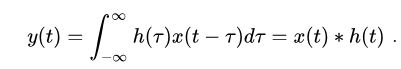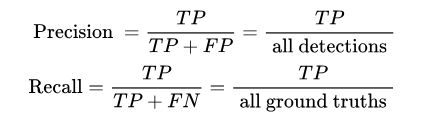机器学习、深度学习面试问题

1.Logistic Regression and Linear Regression 参考

线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。https://blog.csdn.net/out_of_memory_error/article/details/81262309

优点：结果易于理解，计算上不复杂。
缺点：对非线性数据拟合不好。
适用数据类型：数值型和标称型数据。
算法类型：回归算法

优化方法：

使用线性回归的数据符合高斯分布。缺乏实数上分布的先验知识, 不知选择何种形式时, 默认选择正态分布总是不会错的,因为中⼼极限定理告诉我们, 很多独立随机变量均近似服从正态分布。

Logistic regression:logistic回归会在线性回归后再加一层logistic函数的调用。

https://github.com/zergtant/pytorch-handbook/blob/master/chapter3/3.1-logistic-regression.ipynb

损失函数：

梯度优化：

优点：

1、实现简单；

2、分类时计算量非常小，速度很快，存储资源低；

缺点：

1、容易欠拟合，一般准确度不太高

2、只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分；

适用数据类型：数值型和标称型数据。
类别：分类算法。
试用场景：解决二分类问题。

LR分类为什么不使用MSE，因为分类中会使用非线性函数Sigmoid，且求导中会出现使得梯度消失的项（只有在深度较深的模型中才会存在梯度消失），其实主要因为任务的性质不同，一个是对连续数据做出预测，一个是对离散数据做出预测。下图是在模型较深的情况下：

使用逻辑回归的数据符合伯努利分布（0-1分布），适合对离散型随机变量建模。注二项分布指的是n重伯努利成功的次数的离散概率分布。

逻辑回归用于多分类：one vs rest方法，one vs one 方法，softmax。https://zhuanlan.zhihu.com/p/46599015

本质上讲，多分类 就是 logistic 回归进行多分类时的一种数学拓展，如果让分类数为 2 带入多分类，会发现其本质上和 logistic 回归是一样的。Softmax 适合处理一个样本尽可能属于一种类别的多分类问题。

反向传播中，在softmax层也是需要求导的，梯度在经过损失函数后，需要乘上损失softmax的求导项，得到损失函数对输入到softmax的数据的求导。https://blog.csdn.net/yiranlun3/article/details/78632752

#线性回归：
class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1, 1) # 输入和输出的维度都是1
    def forward(self, x):
        out = self.linear(x)
        return out
#逻辑回归：
class LR(nn.Module):
    def __init__(self):
        super(LR,self).__init__()
        self.fc=nn.Linear(24,2) # 由于24个维度已经固定了，所以这里写24
    def forward(self,x):
        out=self.fc(x)
        out=torch.sigmoid(out)
        return out

2.岭回归和Lasso 回归 https://blog.csdn.net/Joker_sir5/article/details/82756089

模型误差 = 偏差（Bias）+ 方差（Variance）+ 数据本身的误差。其中数据本身的误差，可能由于记录过程中的一些不确定性因素等导致，这个我们无法避免，能做的只有不断优化模型参数来权衡偏差和方差，使得模型误差尽可能降到最低。

偏差：导致偏差的原因有多种，其中一个就是针对非线性问题，使用线性方法去求解，当模型欠拟合时，就会出现较大的偏差。

方差：产生高方差的原因通常是由于模型过于复杂，即模型过拟合时，会出现较大的方差。

通常情况下，我们降低了偏差就会相应地使得方差提高，降低了方差就会相应地提高了偏差，所以在机器学习的模型中，我们总是希望找到一组最优的参数，这些参数能权衡模型的偏差和方差，使得模型性能达到最优。

针对高方差，即过拟合的模型，解决办法之一就是对模型进行正则化：限制参数大小。当线性回归过拟合时，权重系数wj就会非常的大，岭回归就是要解决这样的问题。岭回归（Ridge Regression）可以理解为在线性回归的损失函数的基础上，加,入一个L2正则项，来限制W不要过大。其中λ>0，通过确定λ的值可以使得模型在偏差和方差之间达到平衡，随着λ的增大，模型的方差减小，偏差增大。

Lasso回归和岭回归类似，不同的是，Lasso可以理解为在线性回归基础上加入一个L1正则项，同样来限制W不要过大。其中λ>0，通过确定λ的值可以使得模型在偏差和方差之间达到平衡，随着λ的增大，模型的方差减小，偏差增大。Lasso趋向于使得一部分w值变为0，所以可以作为特征选择用，因为这里的L1正则项并不是处处可导的，所以并不能直接使用基于梯度的方法优化损失函数。

3.深度学习模型初始化 参考

我们在线性回归，logistics回归的时候，基本上都是把参数初始化为0，我们的模型也能够很好的工作。然后在神经网络中，把w初始化为0是不可以的。这是因为如果把w初始化0，那么每一层的神经元学到的东西都是一样的（输出是一样的），而且在bp的时候，每一层内的神经元也是相同的，因为他们的gradient相同。

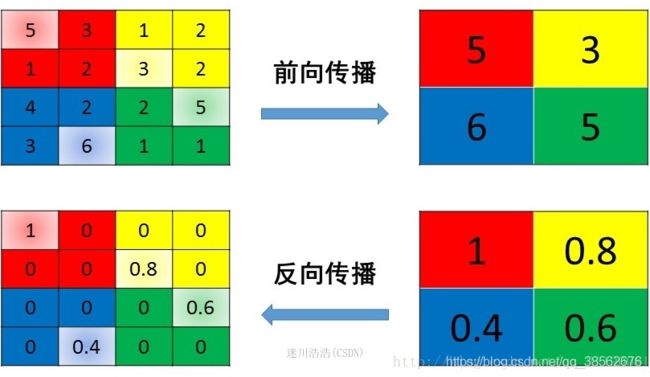
4.池化层的反向传播 参考 参考2

5.感受野计算 参考

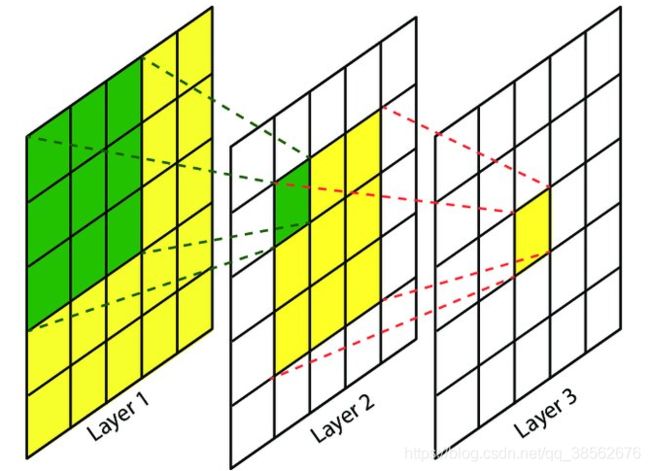
感受野（Receptive Field），指的是神经网络中神经元“看到的”输入区域。

1. 在卷积神经网络中，feature map上某个元素的计算受输入图像上某个区域的影响，这个区域即该元素的感受野。输入到第L层的特征图上的每个元素与第L层的kernel上的单个神经元的感受野一样。
2. 感受野是个相对概念，某层feature map上的元素看到前面不同层上的区域范围是不同的，通常在不特殊指定的情况下，感受野指的是看到输入图像上的区域。

3. 准确计算感受野，需要回答两个子问，即视野中心(感受野位置)在哪和视野范围多大(感受野大小)。

   a.只有看到”合适范围的信息”才可能做出正确的判断，否则就可能“盲人摸象”或者“一览众山小”；(感受野大小)b.目标识别问题中，我们需要知道神经元看到是哪个区域，才能合理推断物体在哪以及判断是什么物体。（感受野位置）

计算感受野的大小，r：receptive field size为r×r，这里假定感受野为方形；根据1，得到的递推公式中没有输入特征图的大小，只与第L层的kernel大小和L-1层卷积的stride(步长)有关。同样根据1，感受野的大小可以看成第L层的kernel上的某个神经元换算成第一层的神经元的大小。

 ，如下图，r1 = 1，r2 = r1+(3-1)*1=3，r3 = r2+(3-1)*1=5。由于后一层的一个神经元的感受野为前一层的K*K=rl-1，也是前一层一个kernel的大小，当前层kernel的单边除第一个元素以外，剩下kl-1个神经元，即kl-1步，如图Layer2的绿色前进一格，相应的输入图像上前进 jl-1格，总的加起来为Layer3单个神经元累计的感受野。注rl代表的是rl*rl的方格。jl-1是stride的累积，连乘。

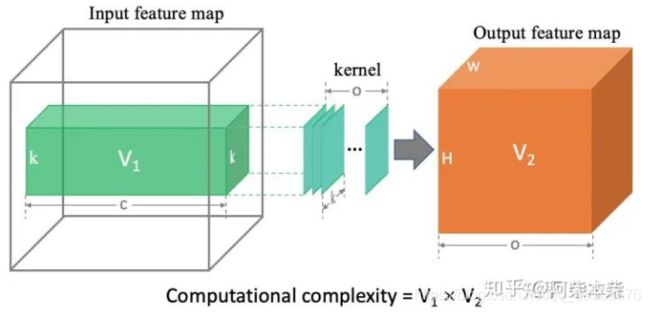
6.FLOPs的计算  https://zhuanlan.zhihu.com/p/137719986

某一层的计算消耗(定义一次flop为一次乘加时)=V1*V2(黄绿体积的乘积)，输出为O张特征图，每张特征图有H*W个点，这O*H*W中的每一个点都需要进行一定的计算获得，即通过一个过滤器进行一次卷积操作获得这样一个点。过滤器进行一次卷积操作即为：c*k*k次乘加。

7.pytorch 多GPU并行训练 参考参考2

单机多卡训练：使用torch.nn.DataParallel()和torch.nn.DistributedDataParallel()。推荐的是torch.nn.DistributedDataParallel()，因为torch.nn.DataParallel()存在负载不均衡的问题，也就是主显卡由于要汇集各个显卡梯度使得显存占用明显较多，使得多卡并行效果不是很好。

torch.nn.DataParallel()，这个类其中有一个module的变量用来保存传入的实际模型。保存的时候直接取出原始的model：

torch.save(model.module.state_dict(), path)

前向：将输入数据和模型分发道各个GPU上，并行前向，将结果汇聚到主线开GPU1上。

后向：计算loss关于输出的梯度，由于没有其他显卡的中间输出特征图，无法算出其他卡的需要的所有梯度。将各个loss关于输出的梯度分发下去,每个模型拿到后计算梯度，进行loss.backward()。然后每个显卡上的梯度汇集道主显卡上相加，进行优化器更新，optimizer.step()，更新主显卡上的梯度。主显卡的模型进行到下一状态，整个流程是将多卡并行来模仿单卡。下一个iteration时为了将其他GPU上的模型的状态进行更新，直接将模型主显卡上的模型replicate下去，这样要比将整个梯度分发下去节省显存

 torch.nn.DistributedDataParallel()对于显卡负载不均衡的问题要轻微一些，另外还可以支持分布式的模型(一个模型太大, 以至于无法放到一个GPU上运行, 需要分开到多个GPU上面执行).

对于多极多卡训练：在单机多gpu可以满足的情况下, 绝对不建议使用多机多gpu进行训练, 网络更不上的话多台机器之间传输数据的时间非常慢。

8.resnet的反向传播梯度推导 参考

9.简单卷积计算的代码实现：参考

def convolution(k, data):
    n,m = data.shape
    img_new = []
    for i in range(n-3):
        line = []
        for j in range(m-3):
            a = data[i:i+3,j:j+3]
            line.append(np.sum(np.multiply(k, a)))
        img_new.append(line)
    return np.array(img_new)

10.BN层的前向，后向python代码实现：参考

使用BN我们完全可以使用较大的学习率加快收敛速度，而且不会影响模型最终的效果。参考

11.知识蒸馏

知识蒸馏中是将教师网络输出的结果作为label给学生网络训练，让学生网络拟合教师网络的输出，实现是在算loss时，在正常的交叉熵后面加上P_师logP_学。还有的是对loss加上其他正则项，比如加上两个模型特征图之间的L2范数，使得产生相应特征图的权重在反向时受到一定约束。

为什么不直接用真实的one hot标签而是教师的预测结果呢，也就是知识蒸馏为什么work？

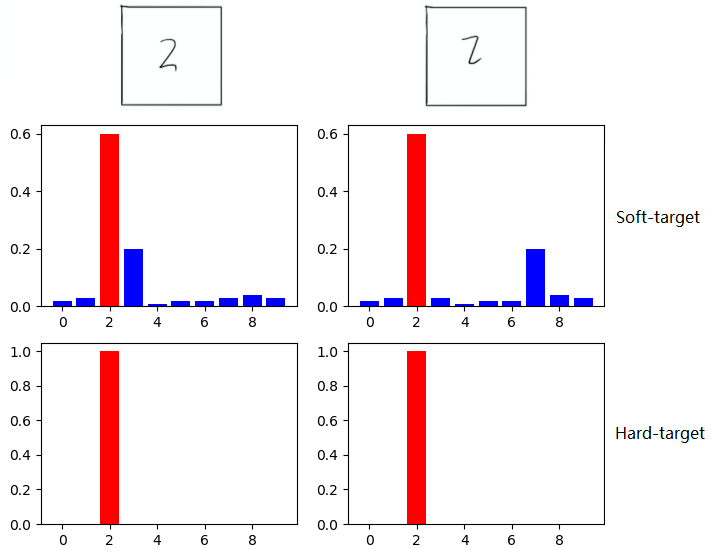
softmax层的输出，除了正例之外，负标签也带有Teacher模型归纳推理的大量信息，比如某些负标签对应的概率远远大于其他负标签，则代表 Teacher模型在推理时认为该样本与该负标签有一定的相似性。而在传统的训练过程(Hard-target)中，所有负标签都被统一对待。也就是说，知识蒸馏的训练方式使得每个样本给Student模型带来的信息量大于传统的训练方式。

如在MNIST数据集中做手写体数字识别任务，假设某个输入的“2”更加形似"3"，softmax的输出值中"3"对应的概率会比其他负标签类别高；而另一个"2"更加形似"7"，则这个样本分配给"7"对应的概率会比其他负标签类别高。这两个"2"对应的Hard-target的值是相同的，但是它们的Soft-target却是不同的，由此我们可见Soft-target蕴含着比Hard-target更多的信息。

在使用 Soft-target 训练时，Student模型可以很快学习到 Teacher模型的推理过程；而传统的 Hard-target 的训练方式，所有的负标签都会被平等对待。因此，Soft-target 给 Student模型带来的信息量要大于 Hard-target，并且Soft-target分布的熵相对高时，其Soft-target蕴含的知识就更丰富。同时，使用 Soft-target 训练时，梯度的方差会更小，训练时可以使用更大的学习率，所需要的样本也更少。这也解释了为什么通过蒸馏的方法训练出的Student模型相比使用完全相同的模型结构和训练数据只使用Hard-target的训练方法得到的模型，拥有更好的泛化能力。

软标签类似训练技巧Label smoothing，提供一种正则化策略，即在标签中加入噪声，减少预测的正标签在计算损失函数时的权重，最终起到拟制过拟合的效果，提升模型的泛化能力。

https://blog.csdn.net/qq_43211132/article/details/100510113

https://mp.weixin.qq.com/s/_Oa4ouuk4uxBK1FXK5NhKA

12.贝叶斯公式

https://blog.csdn.net/qq_31073871/article/details/81077386

13.什么是卷积

卷积：直白地说即是融合，是信号在某些维度（比如时间，空间）上的融合。卷积的三个重要点：同一信号在不同时域上的融合（多维卷积中）；同一信号在不同时域上的融合存在着倍率关系；得到的输出响应即是一个累加的信号。可以从其定义中也可以看出（一维卷积），输出响应是输入在时间上的累加：

扩展到图像中，即二维卷积，是输入图片在空间上的累加融合：

所以不难看出，图像中的卷积的目的即是特征的提取，其加权求和到达特征凸显的过程就是一个融合的过程，从而提取到特征。

14.Dropout层

在训练时，每个神经单元以概率p被保留(dropout丢弃率为1-p)；在测试阶段，每个神经单元都是存在的，权重参数w要乘以p，成为：pw。测试时需要乘上p的原因：考虑第一隐藏层的一个神经元在dropout之前的输出是x，那么dropout之后的期望值是E=px+(1−p)0E=px+(1−p)0 ，在测试时该神经元总是激活，为了保持同样的输出期望值并使下一层也得到同样的结果，需要调整x→pxx→px. 其中p是Bernoulli分布（0-1分布）中值为1的概率。示意图如下：参考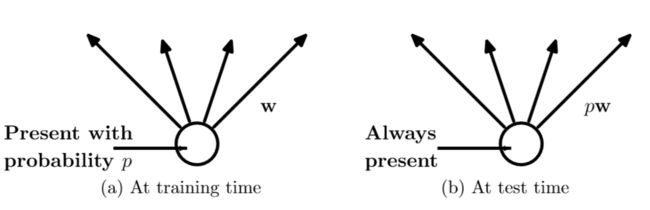

15.详解准确率、精确率、召回率、F1值等评价指标的含义

参考：https://blog.csdn.net/XiaoYi_Eric/article/details/86726284

https://zhuanlan.zhihu.com/p/90744501

首先要确定的是精确率和召回率是二分类算法的评价指标，即关注点在于正例（阳性），F1值是在一些场景下要兼顾两者而设置的，避免此消彼长，准确率的关注点在每个样本是否被预测正确（二类或多类，每个类别都关注）。精确率是针对的预测结果（预测的精确性），即预测结果为正例（目标数据）中有多少真正的正例。召回率关注的是原样本中的正例（目标数据）有多少被找出来了。

精确率高即是找到正例的结果是否精准，确保预测出来的结果尽可能都是TP（真正的正例），减少FP（假的正例），降低误报，比如疾病筛查。

召回率高即是正例有多少被找到，确保更多的TP被找到，减少FN（假的负例），降低漏报，比如要求搜索结果全面等场景下。

因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高。如果是做实验研究，可以绘制Precision-Recall曲线来帮助分析，或使用F1值。

16.YOLO中的置信度的作用

也就是说在train阶段，置信度处于被训练阶段，无实际意义，筛选框使用的是IOU，在test阶段，由于test是没有ground truth，置信度+IOU被用来筛选框即在NMS中。YOLO与two-stage的Faster rcnn这些的一个区别就是yolo设置了置信度这一概念来筛选框而faster rcnn 使用rpn网络来筛选提供框

17.目标检测中的AP，AR，和mAP怎么理解 https://zhuanlan.zhihu.com/p/399837729

其中 all detctions 代表该类别整个数据集中所有预测框的数量， all ground truths 代表该类别整个数据集中所有 GT 的数量，图中的TP/FP/FN为相应的数量，此时不是指代相应类。在划分TP/FP时，我们使用的是一个阈值（IOU或者置信度），因此precision不是一个绝对的东西，而是相对threshold而改变的东西， recall同理， 那么单个用precision来作为标准判断， 就不合适。 这是一场precision与recall之间的trade off， 用一组固定值表述不够全面， 因为我们根据不同的阈值， 可以取到不同（也可能相同）的precision recall值。这样想的话对于每个threshold，我们都有（precision， recall）的pair， 也就有了precision和recall之间的curve关系。

有了这么一条precision-recall curve， 他衡量着两个有价值的判断标准， precision和recall的关系， 那么不如两个一起动态考虑， 就有了鸭子这个class的Average Precision， 即curve下的面积， 他可以充分的表示在这个model中， precision和recall的总体优劣。参考：https://www.zhihu.com/question/53405779/answer/429585383

AP 是计算某一类 P-R 曲线下的面积，mAP 则是计算所有类别 P-R 曲线下面积的平均值，具体计算方式参考： https://www.zhihu.com/question/53405779/answer/993913699   注意：该回答中疏漏，计算AP时，在PR曲线上取每个点右侧最大的Precision作为该点处的Precision，阈值为0.3。

AP是识别的性能的指标，检测是预测框+分类，但这个指标并没有体现预测框的好坏（没有绝对的标准答案），只能计算识别的好坏（因为有绝对的标准答案），相对来说检测更偏向分类更为重要（因为有绝对标准答案）。

18.coco_detection_metrics ——COCO检测指标

Average Precision  (AP) @[ IoU=0.50:0.95 | area=   all | maxDets=100 ] = 0.025
 Average Precision  (AP) @[ IoU=0.50      | area=   all | maxDets=100 ] = 0.078
 Average Precision  (AP) @[ IoU=0.75      | area=   all | maxDets=100 ] = 0.005
 Average Precision  (AP) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000
 Average Precision  (AP) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.045
 Average Precision  (AP) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.018
 Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets=  1 ] = 0.043
 Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets= 10 ] = 0.047
 Average Recall     (AR) @[ IoU=0.50:0.95 | area=   all | maxDets=100 ] = 0.047
 Average Recall     (AR) @[ IoU=0.50:0.95 | area= small | maxDets=100 ] = -1.000
 Average Recall     (AR) @[ IoU=0.50:0.95 | area=medium | maxDets=100 ] = 0.070
 Average Recall     (AR) @[ IoU=0.50:0.95 | area= large | maxDets=100 ] = 0.038

1.Average Precision (AP)和Average Recall (AR)等等这些都是啥意思？

• IoU=0.50意味着IoU大于0.5被认为是检测到。
• IoU=0.50:0.95意味着IoU在0.5到0.95的范围内被认为是检测到。
• 越低的IoU阈值，则判为正确检测的越多，相应的，Average Precision (AP)也就越高。参考上面的第二第三行。
• small表示标注的框面积小于32 * 32；
• medium表示标注的框面积同时小于96 * 96；
• large表示标注的框面积大于等于96 * 96；
• all表示不论大小，我都要。
• maxDets=100表示最大检测目标数为100。
• AP50，AP60，AP70……等等指的是取detector的IoU阈值大于0.5，大于0.6，大于0.7……等等。可以看到数值越高，精确率越低，表明越难。

2. Average Precision (AP)和Average Recall (AR)值里面有-1是什么情况？

参考：https://github.com/cocodataset/cocoapi/blob/master/PythonAPI/pycocotools/cocoeval.py#L52

标注里面没有此类型的目标框，则Average Precision和Average Recall值为-1。

上面的例子中，area= small的Average Precision和Average Recall值为-1，说明验证集中的标注框面积没有小于32 * 32的。

19.IPM变换和相机标定

相机标定的目标是我们找一个合适的数学模型，求出这个模型的参数（将相机比作函数），这样我们能够近似三维场景到二维图像的过程，使这个三维到二维的过程的函数找到反函数。这个逼近的过程就是「相机标定」，我们用简单的数学模型来表达复杂的成像过程，并且求出成像的反过程。标定之后的相机（每个相机的标定参数不同），可以进行三维场景的重建，即深度的感知，这是计算机视觉的一大分支。https://zhuanlan.zhihu.com/p/30813733

IPM变换：在前视摄像头拍摄的图像中，由于透视效应的存在，本来平行的事物，在图像中确实相交的。而IPM变换就是消除这种透视效应，所以也叫逆透视。https://blog.csdn.net/feiyang_luo/article/details/103555036

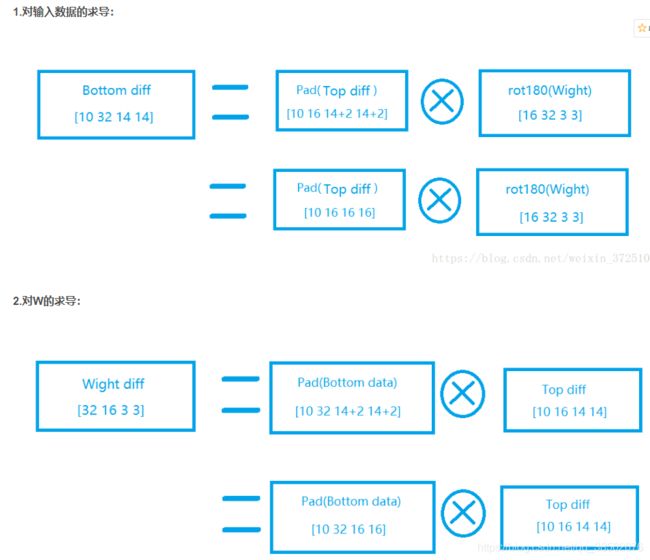
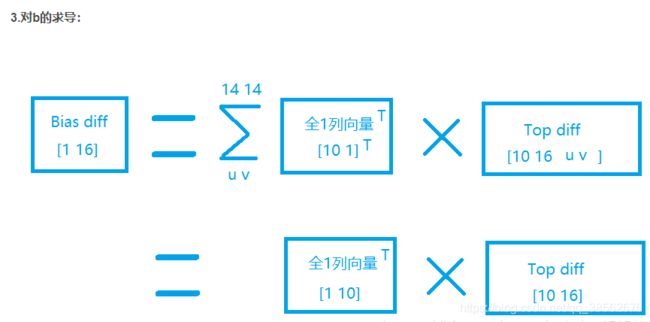
20.卷积层的反向传播

https://blog.csdn.net/weixin_37251044/article/details/81349287

https://www.baidu.com/link?url=LUcYgXnGABWfK_BoXUHQOx51bElEzFq_bSXQh9plfOr1ygUkzT84ANPgdLZQURb_R7hH-5UgN-2npY8hKPn091yVXsiJFPqkODZat6o9k-7&wd=&eqid=902c0e520000051e0000000360b45519

   

池化层的反向传播：https://blog.csdn.net/weixin_37251044/article/details/81328494?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-1&spm=1001.2101.3001.4242

21.模型部署的专栏（商汤）：https://zhuanlan.zhihu.com/p/367042545

22.Focal Loss:https://zhuanlan.zhihu.com/p/80594704

Focal loss主要是为了解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

将样本分类正负和难易，标准二分类的交叉熵函数对置信度较大的样本（即是越接近label的样本）的损失较小，只能正常衡量预测结果与label间的差距，但对具体的样本即样本的正负难易没有针对性的改造。在目标检测中，正负样本中，正样本偏少，难易样本中，难样本偏少，也就是说为了让模型提升性能，对困难样本进行更大力度的学习（特别是正难样本的学习），需要对标准交叉熵函数进行改造。

正负可以通过在交叉熵中对正负样本的损失通过加权进行改善，但是这样存在正难和正易获得相同加权值的问题，因此，Focal Loss对预测出来的置信度进行了进一步的利用，使得正易，负易样本的加权降低，形成加权值大小关系为：正难>负难>正易>负易的局面。

23.为什么单级结构的识别准确度低https://zhuanlan.zhihu.com/p/59910080

目标识别有两大经典结构:

1. 第一类是以Faster RCNN为代表的两级识别方法，这种结构的第一级专注于proposal的提取，第二级则对提取出的proposal进行分类和精确坐标回归。两级结构准确度较高，但因为第二级需要单独对每个proposal进行分类/回归，速度就打了折扣；
2. 第二类结构是以YOLO和SSD为代表的单级结构，它们摒弃了提取proposal的过程（改为人工预先设置的anchor+置信度来提供优质的候选框，最后和二阶一样通过NMS进一步筛选），只用一级就完成了识别/回归，虽然速度较快但准确率远远比不上两级结构。

输入一张图片后的目标占的比例一般都远小于背景占的比例，所以在计算bbox的Loss的时候以Negative example为主，对Loss造成的影响大，把positive的loss淹没掉了，而且negative中有大部分是easynegative，则是背景类（没有物体的话是不计算loss），使得loss较小，影响收敛。

总之在训练阶段，第一，单阶段无法像二阶段那样提供优质的候选框来回归（单阶段人工设置加置信度筛选，二阶段通过RPN或SS来提供+score来筛选）。第二，二阶段在提供候选框后可以通过IOU的阈值来调整positive和negative的比例。在RPN后可以通过IOU大小来调整positive和negative的比例。单阶段无法实现这个过程，因为预测框为negative还是Positive只能在最后训练算Loss时才能知道。两个点总结起来就是单阶段的候选框的优质程度（数量上去平衡和质量）比二阶段差，但是正因为取消proposal才变快的。

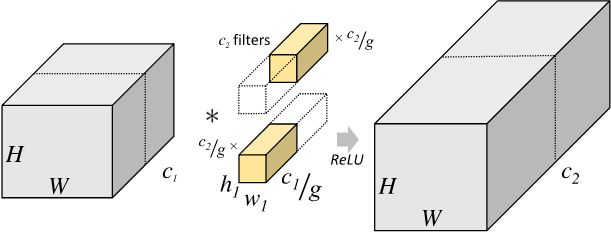
24.分组卷积和深度可分离卷积：https://zhuanlan.zhihu.com/p/65377955

左为标准的卷积计算方式，右为分组卷积，就是将输入进行分组，然后对于每一小组输入，有一个过滤器去卷。相比与标准会有1/g的参数量减少。本质是标准的卷积计算方式是对每张输入特征图进行了过滤器数量次的卷积，但分组卷积中对每张特征图只进行了一次卷积。

25.smooth L1 loss（在L1基础上使得处处可导），L1 loss， L2 loss以及Huber Loss (在L2 loss的基础上避免离群点的影响)

https://www.cnblogs.com/wangguchangqing/p/12021638.html