【机器学习的数学基础】(二)线性代数(Linear Algebra)(中)
文章目录
-
- 2 线性代数(Linear Algebra)(中)
-
- 2.4 向量空间
-
- 2.4.1 群
- 2.4.2 向量空间
- 2.4.3 向量子空间
- 2.5 线性独立
- 2.6 基和秩
-
- 2.6.1 生成集和基
- 2.6.2 秩
2 线性代数(Linear Algebra)(中)
2.4 向量空间
到目前为止,我们已经了解了线性方程组以及如何求解它们(2.3节)。我们看到线性方程组可以用矩阵-向量表示法来表示。下面,我们将更深入地了解向量空间,即向量所在的结构化空间。
在本章的开头,我们非正式地将向量描述为相加并乘以标量后,仍然是相同类型的对象。现在,我们准备将其形式化,我们将首先介绍群的概念,它包含一组元素和一个定义在这些元素上的操作,该操作可以保持集合的某些结构完整。
2.4.1 群
群在计算机科学中扮演着重要的角色。除了为集合上的运算提供一个基本框架外,它们还被大量应用于密码学、编码理论和图形学。
定义 2.7 群
考虑一个集合 G \mathcal{G} G和一个定义在 G \mathcal{G} G上的运算 ⊗ : G × G → G \otimes: \mathcal{G} \times \mathcal{G} \rightarrow \mathcal{G} ⊗:G×G→G。如果下列条件成立,则 G : = ( G , ⊗ ) G:=(\mathcal{G}, \otimes) G:=(G,⊗)称为群(group):
- 1 G \mathcal{G} G在 ⊗ \otimes ⊗运算下的封闭性(Closure): ∀ x , y ∈ G : x ⊗ y ∈ G \forall x, y \in \mathcal{G}: x \otimes y \in \mathcal{G} ∀x,y∈G:x⊗y∈G
- 2 结合律(Associativity): ∀ x , y , z ∈ G : ( x ⊗ y ) ⊗ z = x ⊗ ( y ⊗ z ) \forall x, y, z \in \mathcal{G}:(x \otimes y) \otimes z=x \otimes(y \otimes z) ∀x,y,z∈G:(x⊗y)⊗z=x⊗(y⊗z)
- 3 单位元(Neutral elemen): ∃ e ∈ G ∀ x ∈ G : x ⊗ e = x and e ⊗ x = x \exists e \in \mathcal{G} \forall x \in \mathcal{G}: x \otimes e=x \text { and } e \otimes x=x ∃e∈G∀x∈G:x⊗e=x and e⊗x=x
- 4 逆元(Inverse element): ∀ x ∈ G ∃ y ∈ G : x ⊗ y = e and y ⊗ x = e \forall x \in \mathcal{G} \exists y \in \mathcal{G}: x \otimes y=e \text { and } y \otimes x=e ∀x∈G∃y∈G:x⊗y=e and y⊗x=e,其中 e e e是单位元。我们经常写 x − 1 x^{−1} x−1来表示 x x x的逆元。
备注:
逆元是针对运算 ⊗ ⊗ ⊗定义的,并不一定意味着逆元一定是 1 x \frac{1}{x} x1
另外, ∀ x , y ∈ G : x ⊗ y = y ⊗ x \forall x, y \in \mathcal{G}: x \otimes y=y \otimes x ∀x,y∈G:x⊗y=y⊗x, 那么 G = ( G , ⊗ ) G=(\mathcal{G}, \otimes) G=(G,⊗)是阿贝尔群( Abelian group,即可交换运算顺序的)。
例 2.10群
Z \mathbb{Z} Z:整数; N 0 \mathrm{N}_{0} N0:自然数; R \mathbb{R} R:实数。 C \mathbb{C} C:复数
让我们看一些具有相关操作的集合示例,判断它们是否为群:
-
( Z , + ) (\mathbb{Z},+) (Z,+)是一个阿贝尔群。
-
( N 0 , + ) (\mathrm{N}_{0},+) (N0,+)不是一个群:虽然 ( N 0 , + ) (\mathrm{N}_{0},+) (N0,+)有一个单位元,但是缺少逆元。
-
( Z , ⋅ ) (\mathbb{Z}, \cdot) (Z,⋅)不是群:虽然 ( Z , ⋅ ) (\mathbb{Z}, \cdot) (Z,⋅)包含一个单位元(1),但是任何 z ∈ Z , z ≠ ± 1 z \in \mathbb{Z}, z \neq\pm 1 z∈Z,z=±1的逆元都不是整数。
-
( R , ⋅ ) (\mathbb{R}, \cdot) (R,⋅)不是群,因为0不具有逆元。
-
( R \ { 0 } , ⋅ ) (\mathbb{R} \backslash\{0\}, \cdot) (R\{ 0},⋅)是阿贝尔群。
-
( R n , + ) , ( Z n , + ) , n ∈ N \left(\mathbb{R}^{n},+\right),\left(\mathbb{Z}^{n},+\right), n \in \mathbb{N} (Rn,+),(Zn,+),n∈N是阿贝尔群,前提是 + + +是按分量定义的,即:
( x 1 , ⋯ , x n ) + ( y 1 , ⋯ , y n ) = ( x 1 + y 1 , ⋯ , x n + y n ) \left(x_{1}, \cdots, x_{n}\right)+\left(y_{1}, \cdots, y_{n}\right)=\left(x_{1}+y_{1}, \cdots, x_{n}+y_{n}\right) (x1,⋯,xn)+(y1,⋯,yn)=(x1+y1,⋯,xn+yn)
( x 1 , ⋯ , x n ) − 1 : = ( − x 1 , ⋯ , − x n ) \left(x_{1}, \cdots, x_{n}\right)^{-1}:=\left(-x_{1}, \cdots,-x_{n}\right) (x1,⋯,xn)−1:=(−x1,⋯,−xn)为逆元, e = ( 0 , ⋯ , 0 ) e=(0, \cdots, 0) e=(0,⋯,0)为单位元。 -
( R m × n , + ) \left(\mathbb{R}^{m \times n},+\right) (Rm×n,+), m × n m×n m×n-矩阵集是阿贝尔群(前提是具有上面例子一样的分量加法)。
-
让我们仔细看看 ( R n × n , ⋅ ) \left(\mathbb{R}^{n \times n}, \cdot\right) (Rn×n,⋅),即前文定义的具有矩阵乘法的 n × n n×n n×n-矩阵集。
– 封闭性和结合性直接来自于矩阵乘法的定义。
– 单位元:单位矩阵 I n \boldsymbol{I}_{n} In
– 逆元:如果 A \boldsymbol{A} A的逆存在( A \boldsymbol{A} A是正则的),那么 A − 1 \boldsymbol{A}^{−1} A−1就是 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n的逆元,在这种情况下 ( R n × n , ⋅ ) \left(\mathbb{R}^{n \times n}, \cdot\right) (Rn×n,⋅)就是一个群,称为一般线性群(general linear group)。
定义 2.8一般线性群
正则(可逆)矩阵集 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n关于矩阵乘法的群,称为一般线性群 G L ( n , R ) G L(n, \mathbb{R}) GL(n,R)。然而,由于矩阵乘法是不可交换的,所以该群不是阿贝尔群。
2.4.2 向量空间
当我们讨论群时,我们研究了集合 G \mathcal{G} G的内部运算,即 G \mathcal{G} G内部元素运算的映射 G × G → G \mathcal{G} \times \mathcal{G} \rightarrow \mathcal{G} G×G→G。在下面,我们将考虑除了内部运算( inner operation)“ + + +”外的外部运算(outer operation)“ ⋅ · ⋅”:向量 x ∈ G x \in \mathcal{G} x∈G乘以一个标量 λ ∈ R \lambda \in \mathbb{R} λ∈R。我们可以把内部运算看作是加法的形式,外部运算看作是缩放的形式。请注意,内部/外部操作与内积/外积无关。
定义 2.9向量空间
实值向量空间(Vector Space) V = ( V , + , ⋅ ) V=(\mathcal{V},+,\cdot) V=(V,+,⋅)是一个有两类运算的集合 V \mathcal{V} V
+ : V × V → V +: \mathcal{V} \times \mathcal{V} \rightarrow \mathcal{V} +:V×V→V
⋅ : R × V → V \cdot :\mathbb{R} \times \mathcal{V} \rightarrow \mathcal{V} ⋅:R×V→V
其中
1 ( V , + ) (\mathcal{V},+) (V,+)是阿贝尔群
2 分配律:
∀ λ ∈ R , x , y ∈ V : λ ⋅ ( x + y ) = λ ⋅ x + λ ⋅ y \forall \lambda \in \mathbb{R}, \boldsymbol{x}, \boldsymbol{y} \in \mathcal{V}: \lambda \cdot(\boldsymbol{x}+\boldsymbol{y})=\lambda \cdot \boldsymbol{x}+\lambda \cdot \boldsymbol{y} ∀λ∈R,x,y∈V:λ⋅(x+y)=λ⋅x+λ⋅y
∀ λ , ψ ∈ R , x ∈ V : ( λ + ψ ) ⋅ x = λ ⋅ x + ψ ⋅ x \forall \lambda, \psi \in \mathbb{R}, \boldsymbol{x} \in \mathcal{V}:(\lambda+\psi) \cdot \boldsymbol{x}=\lambda \cdot \boldsymbol{x}+\psi \cdot \boldsymbol{x} ∀λ,ψ∈R,x∈V:(λ+ψ)⋅x=λ⋅x+ψ⋅x
3 结合律(外部操作): ∀ λ , ψ ∈ R , x ∈ V : λ ⋅ ( ψ ⋅ x ) = ( λ ψ ) ⋅ x \forall \lambda, \psi \in \mathbb{R}, \boldsymbol{x} \in \mathcal{V}: \lambda \cdot(\psi \cdot \boldsymbol{x})=(\lambda \psi) \cdot \boldsymbol{x} ∀λ,ψ∈R,x∈V:λ⋅(ψ⋅x)=(λψ)⋅x
4 关于外部操作的单位元: ∀ x ∈ V : 1 ⋅ x = x \forall \boldsymbol{x} \in \mathcal{V}: 1 \cdot \boldsymbol{x}=\boldsymbol{x} ∀x∈V:1⋅x=x
元素 x ∈ V \boldsymbol{x} \in V x∈V称为向量。 ( V , + ) (\mathcal{V},+) (V,+)的单位元是零向量 0 = [ 0 , … , 0 ] ⊤ \mathbf{0}=[0, \ldots, 0]^{\top} 0=[0,…,0]⊤,内部运算 + + +称为向量加法(vector addition)。元素 λ ∈ R \lambda \in \mathbb{R} λ∈R称为标量(scalars),外部运算“ ⋅ · ⋅”是被标量乘(multiplication by scalars)。注意标量积( scalar product)与这是不同的,这在3.2节中会讲。
备注:
“向量乘法(vector multiplication)” a b , a , b ∈ R n \boldsymbol{a b}, \boldsymbol{a}, \boldsymbol{b} \in \mathbb{R}^{n} ab,a,b∈Rn是没有定义的。理论上,我们可以定义一个按元素的乘法,比如 c = a b \boldsymbol{c}=\boldsymbol{a b} c=ab,其中 c j = a j b j c_j=a_j b_j cj=ajbj。这种“数组乘法(array multiplication)”在许多编程语言中都很常见,但这使得用矩阵乘法的标准规则在数学意义上有限:通过将向量视为 n × 1 n×1 n×1矩阵(我们通常这样做),我们可以使用2.3节定义的矩阵乘法进行运算。可这样的话,向量与向量直接相乘的维数却不匹配。仅以下向量乘法有定义: a b ⊤ ∈ R n × n \boldsymbol{a} \boldsymbol{b}^{\top} \in \mathbb{R}^{n \times n} ab⊤∈Rn×n(外积,outer product), a ⊤ b ∈ R \boldsymbol{a}^{\top} \boldsymbol{b} \in \mathbb{R} a⊤b∈R(内积/标量积/点积inner/scalar/dot product)
例 2.11 向量空间
让我们看看一些重要的例子:
-
V = R n , n ∈ N \mathcal{V}=\mathbb{R}^{n}, n \in \mathbb{N} V=Rn,n∈N是一个向量空间,其运算定义如下:
– 相加:对于所有 x , y ∈ R n \boldsymbol{x}, \boldsymbol{y} \in \mathbb{R}^{n} x,y∈Rn, x + y = ( x 1 , … , x n ) + ( y 1 , … , y n ) = ( x 1 + y 1 , … , x n + y n ) \boldsymbol{x}+\boldsymbol{y}=\left(x_{1}, \ldots, x_{n}\right)+\left(y_{1}, \ldots, y_{n}\right)=\left(x_{1}+y_{1}, \ldots, x_{n}+y_{n}\right) x+y=(x1,…,xn)+(y1,…,yn)=(x1+y1,…,xn+yn)
– 与标量相乘:对于所有 λ ∈ R , x ∈ R n \lambda \in \mathbb{R}, \boldsymbol{x} \in \mathbb{R}^{n} λ∈R,x∈Rn, λ x = λ ( x 1 , … , x n ) = ( λ x 1 , … , λ x n ) \lambda \boldsymbol{x}=\lambda\left(x_{1}, \ldots, x_{n}\right)=\left(\lambda x_{1}, \ldots, \lambda x_{n}\right) λx=λ(x1,…,xn)=(λx1,…,λxn) -
V = R m × n , m , n ∈ N \mathcal{V}=\mathbb{R}^{m \times n}, m, n \in \mathbb{N} V=Rm×n,m,n∈N是一个向量空间
– 相加:对于 A , B ∈ V A, B \in \mathcal{V} A,B∈V逐元素相加 A + B = [ a 11 + b 11 ⋯ a 1 n + b 1 n ⋮ ⋮ a m 1 + b m 1 ⋯ a m n + b m n ] \boldsymbol{A}+\boldsymbol{B}=\left[\begin{array}{ccc}a_{11}+b_{11} & \cdots & a_{1 n}+b_{1 n} \\\vdots & & \vdots \\a_{m 1}+b_{m 1} & \cdots & a_{m n}+b_{m n}\end{array}\right] A+B=⎣⎢⎡a11+b11⋮am1+bm1⋯⋯a1n+b1n⋮amn+bmn⎦⎥⎤
– 与标量相乘: λ A = [ λ a 11 ⋯ λ a 1 n ⋮ ⋮ λ a m 1 ⋯ λ a m n ] \lambda \boldsymbol{A}=\left[\begin{array}{ccc}\lambda a_{11} & \cdots & \lambda a_{1 n} \\\vdots & & \vdots \\\lambda a_{m 1} & \cdots & \lambda a_{m n}\end{array}\right] λA=⎣⎢⎡λa11⋮λam1⋯⋯λa1n⋮λamn⎦⎥⎤,记住 R m × n \mathbb{R}^{m \times n} Rm×n相当于 R m n \mathbb{R}^{m n} Rmn。 -
V = C \mathcal{V}=\mathbb{C} V=C也是一个向量空间。
备注:
在下面,当 + + +和 ⋅ · ⋅是标准向量加法和标量乘法时,我们将用 V V V表示向量空间 ( V , + , ⋅ ) (\mathcal{V},+, \cdot) (V,+,⋅)。此外,我们将使用符号 x ∈ V \boldsymbol{x} \in V x∈V表示 V \mathcal{V} V中的向量,以简化符号。
备注:
向量空间 R n , R n × 1 , R 1 × n \mathbb{R}^{n}, \mathbb{R}^{n \times 1}, \mathbb{R}^{1 \times n} Rn,Rn×1,R1×n只是我们写向量的方式不同。在下文中,我们将不区分 R n \mathbb{R}^{n} Rn和 R n × 1 \mathbb{R}^{n \times 1} Rn×1,这允许我们将 n n n元组用列向量( column vectors)表示
x = [ x 1 ⋮ x n ] \boldsymbol{x}=\left[\begin{array}{c}x_{1} \\\vdots \\x_{n}\end{array}\right] x=⎣⎢⎡x1⋮xn⎦⎥⎤
这简化了向量空间运算的表示法。但是,我们确实要区分了 R n × 1 \mathbb{R}^{n \times 1} Rn×1和 R 1 × n \mathbb{R}^{1 \times n} R1×n(行向量row vectors),以避免在使用矩阵乘法时混淆。默认情况下,我们写 x \boldsymbol{x} x来表示列向量,行向量则由 x ⊤ \boldsymbol{x}^{\top} x⊤表示,为列向量的转置。
2.4.3 向量子空间
下面,我们将介绍向量子空间。直观地说,它们是原始向量空间中的集合,且具有这样的性质:我们对子空间的元素进行向量空间运算,结果不会超出子空间。从这个意义上说,它们是“封闭的”。向量子空间是机器学习中的一个重要概念。例如,第10章展示了如何使用向量子空间进行降维。
定义 2.10向量子空间
令 V = ( V , + , ⋅ ) V=(\mathcal{V},+, \cdot) V=(V,+,⋅)为向量空间,且 U ⊆ V , U ≠ ∅ \mathcal{U} \subseteq \mathcal{V}, \mathcal{U} \neq \emptyset U⊆V,U=∅,如果 U U U是一个向量空间,且它的向量空间运算“ + + +”和“ ⋅ · ⋅”限制为 U × U \mathcal{U} \times \mathcal{U} U×U和 R × U \mathbb{R} \times \mathcal{U} R×U,那么 U = ( U , + , ⋅ ) U=(\mathcal{U},+, \cdot) U=(U,+,⋅)称为 V V V的向量子空间(vector subspace,或linear subspace)。我们用 U ⊆ V U⊆V U⊆V来表示 V V V的子空间 U U U。
如果 U ⊆ V U \subseteq V U⊆V(书中 U ⊆ V \mathcal{U} \subseteq \mathcal{V} U⊆V可能有误)且 V V V是向量空间,那么 U U U自然地直接从 V V V继承了许多性质,因为这些性质适用于所有 x ∈ V x∈\mathcal{V} x∈V,特别是所有 x ∈ U ⊆ V \boldsymbol{x} \in \mathcal{U} \subseteq \mathcal{V} x∈U⊆V。这包括阿贝尔群的性质、分配律、结合律和基元。为了确定 ( U , + , ⋅ ) (\mathcal{U},+, \cdot) (U,+,⋅)是否是 V V V的子空间,我们还需要确定:
1 U ≠ ∅ \mathcal{U} \neq \emptyset U=∅,特别地,单位元 0 ∈ U \boldsymbol{0}\in \mathcal{U} 0∈U
2 U U U的封闭性:
- 关于外部操作: ∀ λ ∈ R ∀ x ∈ U : λ x ∈ U \forall \lambda \in \mathbb{R} \forall \boldsymbol{x} \in \mathcal{U}: \lambda \boldsymbol{x} \in \mathcal{U} ∀λ∈R∀x∈U:λx∈U
- 关于内部操作: ∀ x , y ∈ U : x + y ∈ U \forall x, y \in \mathcal{U}: x+y \in \mathcal{U} ∀x,y∈U:x+y∈U
例 2.12 向量子空间
让我们来看一些例子:
-
对于每个向量空间 V V V,其平凡子空间( trivial subspaces)是 V V V本身和 0 {\boldsymbol{0}} 0
-
图2.6中只有示例 D D D是 R 2 \mathbb{R}^{2} R2的子空间(包含内部/外部操作)。在 A A A和 C C C中,违反了封闭性;而 B B B不包含 0 \boldsymbol{0} 0。
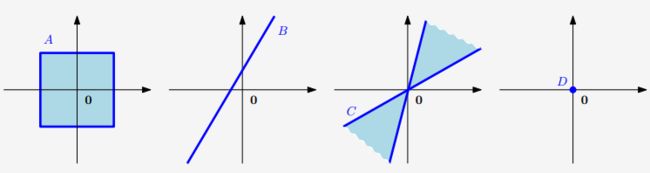
图 2.6不是所有的 R 2 \mathbb{R}^2 R2子集都是子空间。 A A A和 C C C违反了封闭性; B B B不包含 0 \boldsymbol{0} 0。只有 D D D是子空间。 -
具有 n n n个未知量 x = [ x 1 , … , x n ] ⊤ \boldsymbol{x}=\left[x_{1}, \ldots, x_{n}\right]^{\top} x=[x1,…,xn]⊤的齐次线性方程组 A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0的解集是 R n \mathbb{R}^{n} Rn的一个子空间
. -
非齐次线性方程组 A z = b , b ≠ 0 \boldsymbol{A}\boldsymbol{z}=\boldsymbol{b},\boldsymbol{b}\not = \boldsymbol{0} Az=b,b=0的解不是 R n \mathbb{R}^{n} Rn的子空间
-
任意子空间的交集是它们本身的一个子空间。
备注:
对于 x ∈ R n \boldsymbol{x} \in \mathbb{R}^{n} x∈Rn,每个子空间 U ⊆ ( R n , + , ⋅ ) U \subseteq\left(\mathbb{R}^{n},+, \cdot\right) U⊆(Rn,+,⋅)是齐次线性方程组 A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0的解空间
2.5 线性独立
下面我们来看看我们可以用向量(向量空间的元素)做什么。从前文我们知道,我们将向量相加,然后用标量相乘,封闭性能保证我们在同一个向量空间中得到另一个向量。那么有没有可能找到一组向量,允许我们可以用这些向量相加并缩放后得到向量空间中的其他所有向量?实际上,这组向量是一组基(basis),我们将在后面讨论它。在此之前,我们需要介绍一下线性组合和线性独立。
定义 2.11线性组合
考虑向量空间 V V V和有限个向量 x 1 , … , x k ∈ V x_{1}, \ldots, x_{k} \in V x1,…,xk∈V。那么,每一个以下形式的向量 v ∈ V \boldsymbol{v} \in V v∈V:
v = λ 1 x 1 + ⋯ + λ k x k = ∑ i = 1 k λ i x i ∈ V \boldsymbol{v}=\lambda_{1} \boldsymbol{x}_{1}+\cdots+\lambda_{k} \boldsymbol{x}_{k}=\sum_{i=1}^{k} \lambda_{i} \boldsymbol{x}_{i} \in V v=λ1x1+⋯+λkxk=i=1∑kλixi∈V
称为向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk的线性组合(linear combination),其中 λ 1 , … , λ k ∈ R \lambda_{1}, \ldots, \lambda_{k} \in \mathbb{R} λ1,…,λk∈R。
0 \boldsymbol{0} 0向量总是可以写成 k k k个向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk的线性组合,因为 0 = ∑ i = 1 k 0 x i \mathbf{0}=\sum_{i=1}^{k} 0 \boldsymbol{x}_{i} 0=∑i=1k0xi总是成立。在下文中,我们关注一组向量的非平凡线性组合来表示 0 \boldsymbol{0} 0,即:向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk在系数 λ i λ_i λi不都为0的情况下的线性组合。
定义 2.12线性相关与线性无关(独立)
考虑一个向量空间 V V V,且有 x 1 , … , x k ∈ V , k ∈ N \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} \in V,k \in \mathbb{N} x1,…,xk∈V,k∈N。如果存在一个非平凡的线性组合,使得 0 = ∑ i = 1 k λ i x i \boldsymbol{0}=\sum_{i=1}^{k} \lambda_{i} \boldsymbol{x}_{i} 0=∑i=1kλixi,即其中至少有一个 λ i ≠ 0 \lambda_{i} \neq 0 λi=0,则向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk是线性相关的(linearly dependent)。如果只有平凡解存在,即: λ 1 = … = λ k = 0 \lambda_{1}=\ldots=\lambda_{k}=0 λ1=…=λk=0,则向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk是线性独立( linearly independent)。
线性独立是线性代数中最重要的概念之一。直观地说,一组线性无关的向量是由没有冗余的向量组成的,也就是说,如果我们把这些向量中的任何一个去掉,我们就会失去一些东西。在接下来的几节中,我们将进一步形式化这种直觉。
例 2.13 线性相关的向量
一个地理例子可能有助于理解线性独立的概念。如图2.7所示,在 Nairobi (Kenya)的人描述Kigali (Rwanda)所在地可能会说,“你可以先往西北方向506公里到Kampala (Uganda),然后往西南方向374公里”。这足以说明 Kigali的位置,因为地理坐标系可被视为二维向量空间(忽略海拔和地球曲面)。这个人可能会补充说,“大约在西边751公里处“。尽管最后一句话是对的,但鉴于前面的信息,这句话没有必要说。在此示例中,“506 km西北”矢量(蓝色)和“374 km西南”矢量(紫色)是线性独立的。这意味着西南方向的矢量不能用西北方向的矢量来描述,反之亦然。然而,第三个“751 km west”向量(黑色)是其他两个向量的线性组合,这使得这三个向量线性相关。同样地,给定“西751公里”和“西南374公里”,可以线性组合得到“西北506公里”。

图2.7 二维空间(平面)中线性相关向量的地理示例(基本方向的粗略近似)。
备注:以下属性可用于确定向量是否线性独立:
- k k k个向量要么线性相关,要么线性无关。没有第三种选择。
- 向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk中只要有一个零向量或有两个向量相同,则它们是线性相关的。
- 向量 { x 1 , … , x k : x i ≠ 0 , i = 1 , … , k } , k ⩾ 2 \left\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k}: \boldsymbol{x}_{i} \neq \mathbf{0}, i=1, \ldots, k\right\}, k \geqslant 2 { x1,…,xk:xi=0,i=1,…,k},k⩾2,是线性相关的当且仅当(至少)其中一个是其他的线性组合。特别是,如果一个向量是另一个向量的倍数,即: x i = λ x j , λ ∈ R \boldsymbol{x}_{i}=\lambda \boldsymbol{x}_{j}, \lambda \in \mathbb{R} xi=λxj,λ∈R,那么集合 { x 1 , … , x k : x i ≠ 0 , i = 1 , … , k } \left\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k}: \boldsymbol{x}_{i} \neq \mathbf{0}, i=1, \ldots, k\right\} { x1,…,xk:xi=0,i=1,…,k}是线性相关的。
- 检验向量 x 1 , … , x k ∈ V \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} \in V x1,…,xk∈V是线性无关的有效方法是采用高斯消元法:将所有向量写为矩阵 A \boldsymbol{A} A的列,并进行高斯消元,直到矩阵为行阶梯型(这里不需要行最简阶梯型):
– 主元列表示与左侧的向量线性无关的向量。请注意在构建矩阵时对向量排序。
– 非主元列可以表示为其左侧主元列的线性组合。例如,行阶梯型矩阵
[ 1 3 0 0 0 2 ] \left[\begin{array}{lll}1 & 3 & 0 \\0 & 0 & 2\end{array}\right] [103002]
告诉我们第一列和第三列是主元列。第二列是非主元列,它是第一列的三倍。
当且仅当所有列都是主元列时,所有列向量才是线性独立的。尽管只有一个非主元列,这些列(以及相应的向量)也是线性相关的。
例 2.14
考虑 R 4 \mathbb{R}^{4} R4以及向量:
x 1 = [ 1 2 − 3 4 ] , x 2 = [ 1 1 0 2 ] , x 3 = [ − 1 − 2 1 1 ] \boldsymbol{x}_{1}=\left[\begin{array}{c}1 \\2 \\-3 \\4\end{array}\right], \quad \boldsymbol{x}_{2}=\left[\begin{array}{l}1 \\1 \\0 \\2\end{array}\right], \quad \boldsymbol{x}_{3}=\left[\begin{array}{c}-1 \\-2 \\1 \\1\end{array}\right] x1=⎣⎢⎢⎡12−34⎦⎥⎥⎤,x2=⎣⎢⎢⎡1102⎦⎥⎥⎤,x3=⎣⎢⎢⎡−1−211⎦⎥⎥⎤
为了检验它们是否是线性相关的,对于 λ 1 , … , λ 3 \lambda_{1}, \ldots, \lambda_{3} λ1,…,λ3,我们采用一般的方法求解
λ 1 x 1 + λ 2 x 2 + λ 3 x 3 = λ 1 [ 1 2 − 3 4 ] + λ 2 [ 1 1 0 2 ] + λ 3 [ − 1 − 2 1 1 ] = 0 \lambda_{1} \boldsymbol{x}_{1}+\lambda_{2} \boldsymbol{x}_{2}+\lambda_{3} \boldsymbol{x}_{3}=\lambda_{1}\left[\begin{array}{c}1 \\2 \\-3 \\4\end{array}\right]+\lambda_{2}\left[\begin{array}{l}1 \\1 \\0 \\2\end{array}\right]+\lambda_{3}\left[\begin{array}{c}-1 \\-2 \\1 \\1\end{array}\right]=\mathbf{0} λ1x1+λ2x2+λ3x3=λ1⎣⎢⎢⎡12−34⎦⎥⎥⎤+λ2⎣⎢⎢⎡1102⎦⎥⎥⎤+λ3⎣⎢⎢⎡−1−211⎦⎥⎥⎤=0
我们将向量 x i , i = 1 , 2 , 3 \boldsymbol{x}_{i}, i=1,2,3 xi,i=1,2,3作为矩阵的列,并应用初等行变换,直到我们确定主元列:
[ 1 1 − 1 2 1 − 2 − 3 0 1 4 2 1 ] ⇝ ⋯ ⇝ [ 1 1 − 1 0 1 0 0 0 1 0 0 0 ] \left[\begin{array}{ccc}1 & 1 & -1 \\2 & 1 & -2 \\-3 & 0 & 1 \\4 & 2 & 1\end{array}\right] \quad \rightsquigarrow \cdots \rightsquigarrow \quad\left[\begin{array}{ccc}1 & 1 & -1 \\0 & 1 & 0 \\0 & 0 & 1 \\0 & 0 & 0\end{array}\right] ⎣⎢⎢⎡12−341102−1−211⎦⎥⎥⎤⇝⋯⇝⎣⎢⎢⎡10001100−1010⎦⎥⎥⎤
这里,矩阵的每一列都是主元列。因此,不存在非平凡解,只有 λ 1 = 0 , λ 2 = 0 , λ 3 = 0 \lambda_{1}=0, \lambda_{2}=0, \lambda_{3}=0 λ1=0,λ2=0,λ3=0为方程组的解。因此,向量 x l , x 2 , x 3 \boldsymbol{x}_{\mathrm{l}}, \boldsymbol{x}_{2}, \boldsymbol{x}_{3} xl,x2,x3是线性独立的。
备注:
考虑一个向量空间 V V V与其中 k k k个线性无关的向量 b 1 , … , b k \boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{k} b1,…,bk和 m m m种线性组合
x 1 = ∑ i = 1 k λ i 1 b i ⋮ x m = ∑ i = 1 k λ i m b i \begin{aligned}\boldsymbol{x}_{1} &=\sum_{i=1}^{k} \lambda_{i 1} \boldsymbol{b}_{i} \\& \vdots \\\boldsymbol{x}_{m} &=\sum_{i=1}^{k} \lambda_{i m} \boldsymbol{b}_{i}\end{aligned} x1xm=i=1∑kλi1bi⋮=i=1∑kλimbi
定义矩阵 B = [ b 1 , … , b k ] \boldsymbol{B}=\left[\boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{k}\right] B=[b1,…,bk],该矩阵的列为线性无关向量 b 1 , … , b k \boldsymbol{b}_{1}, \ldots, \boldsymbol{b}_{k} b1,…,bk,我们可以将上式写成紧凑的形式:
x j = B λ j , λ j = [ λ 1 j ⋮ λ k j ] , j = 1 , … , m \boldsymbol{x}_{j}=\boldsymbol{B} \boldsymbol{\lambda}_{j}, \quad \boldsymbol{\lambda}_{j}=\left[\begin{array}{c}\lambda_{1 j} \\\vdots \\\lambda_{k j}\end{array}\right], \quad j=1, \ldots, m xj=Bλj,λj=⎣⎢⎡λ1j⋮λkj⎦⎥⎤,j=1,…,m
我们想检验 x 1 , … , x m \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{m} x1,…,xm是否线性无关。为此,我们遵循 ∑ j = 1 m ψ j x j = 0 \sum_{j=1}^{m} \psi_{j} \boldsymbol{x}_{j}=\mathbf{0} ∑j=1mψjxj=0的一般测试方法。我们可以进一步得到:
∑ j = 1 m ψ j x j = ∑ j = 1 m ψ j B λ j = B ∑ j = 1 m ψ j λ j \sum_{j=1}^{m} \psi_{j} \boldsymbol{x}_{j}=\sum_{j=1}^{m} \psi_{j} \boldsymbol{B} \boldsymbol{\lambda}_{j}=\boldsymbol{B} \sum_{j=1}^{m} \psi_{j} \boldsymbol{\lambda}_{j} j=1∑mψjxj=j=1∑mψjBλj=Bj=1∑mψjλj
这意味着 { x 1 , … , x m } \left\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{m}\right\} { x1,…,xm}是线性无关的当且仅当列向量 { λ 1 , … , λ m } \left\{\boldsymbol{\lambda}_{1}, \ldots, \boldsymbol{\lambda}_{m}\right\} { λ1,…,λm}是线性无关。
备注:
在向量空间 V V V中,当 m > k m>k m>k时, k k k个向量 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk的 m m m个线性组合是线性相关的。
例 2.15
考虑一组线性无关向量 b 1 , b 2 , b 3 , b 4 ∈ R n \boldsymbol{b}_{1}, \boldsymbol{b}_{2}, \boldsymbol{b}_{3}, \boldsymbol{b}_{4} \in \mathbb{R}^{n} b1,b2,b3,b4∈Rn,有:
x 1 = b 1 − 2 b 2 + b 3 − b 4 x 2 = − 4 b 1 − 2 b 2 + 4 b 4 x 3 = 2 b 1 + 3 b 2 − b 3 − 3 b 4 x 4 = 17 b 1 − 10 b 2 + 11 b 3 + b 4 \begin{aligned} \boldsymbol{x}_{1}&=&\boldsymbol{b}_{1} &-&2&\boldsymbol{b}_{2}&+&\boldsymbol{b}_{3} &-&\boldsymbol{b}_{4} \\\boldsymbol{x}_{2}&=&-4 \boldsymbol{b}_{1} &-&{2} &\boldsymbol{b}_{2} &&&+&4 \boldsymbol{b}_{4} \\\boldsymbol{x}_{3} &=&2 \boldsymbol{b}_{1}&+&3 \boldsymbol{b}_{2}&-&\boldsymbol{b}_{3} &-& 3 \boldsymbol{b}_{4} \\\boldsymbol{x}_{4} &=&17 \boldsymbol{b}_{1}&-&10 \boldsymbol{b}_{2}&+&11 \boldsymbol{b}_{3}&+&\boldsymbol{b}_{4}\end{aligned} x1x2x3x4====b1−4b12b117b1−−+−223b210b2b2b2−++b311b3b3−+−+3b4b4b44b4
向量是 x 1 , … , x 4 ∈ R n \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{4} \in \mathbb{R}^{n} x1,…,x4∈Rn是否线性无关呢?为了回答这个问题,我们来看看以下列向量
{ [ 1 − 2 1 − 1 ] , [ − 4 − 2 0 4 ] , [ 2 3 − 1 − 3 ] , [ 17 − 10 11 1 ] } \left\{\left[\begin{array}{c}1 \\-2 \\1 \\-1\end{array}\right],\left[\begin{array}{c}-4 \\-2 \\0 \\4\end{array}\right],\left[\begin{array}{c}2 \\3 \\-1 \\-3\end{array}\right],\left[\begin{array}{c}17 \\-10 \\11 \\1\end{array}\right]\right\} ⎩⎪⎪⎨⎪⎪⎧⎣⎢⎢⎡1−21−1⎦⎥⎥⎤,⎣⎢⎢⎡−4−204⎦⎥⎥⎤,⎣⎢⎢⎡23−1−3⎦⎥⎥⎤,⎣⎢⎢⎡17−10111⎦⎥⎥⎤⎭⎪⎪⎬⎪⎪⎫
是否线性无关。
线性方程组对应的矩阵为:
A = [ 1 − 4 2 17 − 2 − 2 3 − 10 1 0 − 1 11 − 1 4 − 3 1 ] \boldsymbol{A}=\left[\begin{array}{cccc}1 & -4 & 2 & 17 \\-2 & -2 & 3 & -10 \\1 & 0 & -1 & 11 \\-1 & 4 & -3 & 1\end{array}\right] A=⎣⎢⎢⎡1−21−1−4−20423−1−317−10111⎦⎥⎥⎤
对应的最简阶梯型矩阵为:
[ 1 0 0 − 7 0 1 0 − 15 0 0 1 − 18 0 0 0 0 ] \left[\begin{array}{cccc}1 & 0 & 0 & -7 \\0 & 1 & 0 & -15 \\0 & 0 & 1 & -18 \\0 & 0 & 0 & 0\end{array}\right] ⎣⎢⎢⎡100001000010−7−15−180⎦⎥⎥⎤
可以看到相应的线性方程组是有非平凡解的:最后一列不是主元列, x 4 = − 7 x 1 − 15 x 2 − 18 x 3 \boldsymbol{x}_{4}=-7 \boldsymbol{x}_{1}-15 \boldsymbol{x}_{2}-18 \boldsymbol{x}_{3} x4=−7x1−15x2−18x3,因此, x 1 , … , x 4 \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{4} x1,…,x4是线性相关的, x 4 \boldsymbol{x}_{4} x4可以表示为 x 1 , … , x 3 \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{3} x1,…,x3的线性组合。
2.6 基和秩
在向量空间 V V V中,我们特别关注的是向量集合 A \mathcal{A} A,这些集合具有这样的性质:任何向量 v ∈ V \boldsymbol{v}\in V v∈V都可以通过 A \mathcal{A} A中向量的线性组合得到。这些向量是特殊的向量,下面我们将对它们进行描述。
2.6.1 生成集和基
定义 2.13 生成集和生成空间
考虑一个向量空间 V = ( V , + , ⋅ ) V=(\mathcal{V},+, \cdot) V=(V,+,⋅)和一个向量集 A = { x 1 , … , x k } ⊆ V \mathcal{A}=\left\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k}\right\} \subseteq \mathcal{V} A={ x1,…,xk}⊆V。如果每个向量 v ∈ V \boldsymbol{v} \in \mathcal{V} v∈V都可以表示为 x 1 , … , x k \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{k} x1,…,xk的线性组合。则 A \mathcal{A} A称为 V V V的生成集(generating set )。 A \mathcal{A} A中的向量的所有线性组合形成的集合称为 A \mathcal{A} A的生成空间(span)。如果 A \mathcal{A} A张成向量空间 V V V,则记: V = span [ A ] V=\operatorname{span}[\mathcal{A}] V=span[A]或 V = span [ x 1 , … , x k ] V=\operatorname{span}\left[x_{1}, \ldots, x_{k}\right] V=span[x1,…,xk]
生成集是张成向量空间(或子空间)的向量集,即,向量空间(或子空间)中的每个向量都可以表示为生成集中向量的线性组合。下面,我们将更具体地描述向量(子)空间的最小生成集。
定义 2.14 基
考虑向量空间 V = ( V , + , ⋅ ) V=(\mathcal{V},+, \cdot) V=(V,+,⋅)以及 A ⊆ V \mathcal{A} \subseteq\mathcal{V} A⊆V。如果没有更小的集合 A ~ ⊊ A ⊆ V \tilde{\mathcal{A}} \subsetneq \mathcal{A} \subseteq \mathcal{V} A~⊊A⊆V可以生成 V V V,则称 V V V的生成集 A \mathcal{A} A为最小生成集(minimal)。 V V V的每一个线性独立的生成集都是最小生成集,被称为 V V V的基(basis)。
设 V = ( V , + , ⋅ ) V=(\mathcal{V},+, \cdot) V=(V,+,⋅)为向量空间,且 B ⊆ V , B ≠ ∅ \mathcal{B} \subseteq \mathcal{V}, \mathcal{B} \neq \emptyset B⊆V,B=∅。那么,以下描述是等价的:
- B \mathcal{B} B是 V V V的基。
- B \mathcal{B} B是最小生成集。
- B \mathcal{B} B是 V V V中向量的一个最大线性无关集,也就是说,在这个向量集中加上任何其他向量都会使它线性相关。
- 每个向量 x ∈ V \boldsymbol{x} \in V x∈V都是 B \mathcal{B} B中向量的线性组合,且每个线性组合都是唯一的,即
x = ∑ i = 1 k λ i b i = ∑ i = 1 k ψ i b i \boldsymbol{x}=\sum_{i=1}^{k} \lambda_{i} \boldsymbol{b}_{i}=\sum_{i=1}^{k} \psi_{i} \boldsymbol{b}_{i} x=i=1∑kλibi=i=1∑kψibi
其中 λ i , ψ i ∈ R , b i ∈ B \lambda_{i}, \psi_{i} \in \mathbb{R}, \boldsymbol{b}_{i} \in \mathcal{B} λi,ψi∈R,bi∈B,且: λ i = ψ i , i = 1 , … , k \lambda_{i}=\psi_{i}, i=1, \ldots, k λi=ψi,i=1,…,k
例 2.16
-
在 R 3 \mathbb{R}^{3} R3中,规范/标准基(canonical/standard basis)为
B = { [ 1 0 0 ] , [ 0 1 0 ] , [ 0 0 1 ] } \mathcal{B}=\left\{\left[\begin{array}{l}1 \\0 \\0\end{array}\right],\left[\begin{array}{l}0 \\1 \\0\end{array}\right],\left[\begin{array}{l}0 \\0 \\1\end{array}\right]\right\} B=⎩⎨⎧⎣⎡100⎦⎤,⎣⎡010⎦⎤,⎣⎡001⎦⎤⎭⎬⎫ -
R 3 \mathbb{R}^{3} R3中有不唯一的基:
B 1 = { [ 1 0 0 ] , [ 1 1 0 ] , [ 1 1 1 ] } , B 2 = { [ 0.5 0.8 0.4 ] , [ 1.8 0.3 0.3 ] , [ − 2.2 − 1.3 3.5 ] } \mathcal{B}_{1}=\left\{\left[\begin{array}{l}1 \\0 \\0\end{array}\right],\left[\begin{array}{l}1 \\1 \\0\end{array}\right],\left[\begin{array}{l}1 \\1 \\1\end{array}\right]\right\}, \mathcal{B}_{2}=\left\{\left[\begin{array}{l}0.5 \\0.8 \\0.4\end{array}\right],\left[\begin{array}{l}1.8 \\0.3 \\0.3\end{array}\right],\left[\begin{array}{c}-2.2 \\-1.3 \\3.5\end{array}\right]\right\} B1=⎩⎨⎧⎣⎡100⎦⎤,⎣⎡110⎦⎤,⎣⎡111⎦⎤⎭⎬⎫,B2=⎩⎨⎧⎣⎡0.50.80.4⎦⎤,⎣⎡1.80.30.3⎦⎤,⎣⎡−2.2−1.33.5⎦⎤⎭⎬⎫ -
集合
A = { [ 1 2 3 4 ] , [ 2 − 1 0 2 ] , [ 1 1 0 − 4 ] } \mathcal{A}=\left\{\left[\begin{array}{l}1 \\2 \\3 \\4\end{array}\right],\left[\begin{array}{c}2 \\-1 \\0 \\2\end{array}\right],\left[\begin{array}{c}1 \\1 \\0 \\-4\end{array}\right]\right\} A=⎩⎪⎪⎨⎪⎪⎧⎣⎢⎢⎡1234⎦⎥⎥⎤,⎣⎢⎢⎡2−102⎦⎥⎥⎤,⎣⎢⎢⎡110−4⎦⎥⎥⎤⎭⎪⎪⎬⎪⎪⎫
是线性独立的,但不是 R 4 \mathbb{R}^{4} R4的生成集(也不是基):例如,向量 [ 1 , 0 , 0 , 0 ] ⊤ [1,0,0,0]^{\top} [1,0,0,0]⊤不能通过 A \mathcal{A} A中元素的线性组合获得。
备注:
每个向量空间 V V V都有一个基 B \mathcal{B} B。前面的例子表明向量空间 V V V可以有许多基,即没有唯一基。然而,所有的基都由相同数量的元素,即基向量( basis vectors) 组成。
我们只考虑有限维向量空间 V V V。在这种情况下, V V V的维数(dimension) 是 V V V的基向量的个数,我们写成 dim ( V ) \operatorname{dim}(V) dim(V)。如果 V V V的子空间为 U ⊆ V U \subseteq V U⊆V,那么 dim ( U ) ⩽ dim ( V ) \operatorname{dim}(U) \leqslant \operatorname{dim}(V) dim(U)⩽dim(V)。当 U = V U=V U=V时, dim ( U ) = dim ( V ) \operatorname{dim}(U) =\operatorname{dim}(V) dim(U)=dim(V)。直观地说,向量空间的维数可以看作是这个向量空间中独立方向的个数。
备注:
向量空间的维数不一定是向量中元素的个数。 例如,向量空间 V = span [ [ 0 1 ] ] V=\operatorname{span}[\left[\begin{array}{l}0 \\1\end{array}\right]] V=span[[01]]是一维的,尽管基向量有两个元素。
备注:
子空间 U = span [ x 1 , … , x m ] ⊆ R n U=\operatorname{span}\left[\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{m}\right] \subseteq \mathbb{R}^{n} U=span[x1,…,xm]⊆Rn的基可通过执行以下步骤确定:
- 1 把生成向量写成矩阵 A \boldsymbol{A} A的列
- 2 确定 A \boldsymbol{A} A的行阶梯型。
- 3 与主元列对应的生成向量就是 U U U的基。
例 2.17基的确定
向量子空间 U ⊆ R 5 U \subseteq \mathbb{R}^{5} U⊆R5,由以下向量张成:
x 1 = [ 1 2 − 1 − 1 − 1 ] , x 2 = [ 2 − 1 1 2 − 2 ] , x 3 = [ 3 − 4 3 5 − 3 ] , x 4 = [ − 1 8 − 5 − 6 1 ] ∈ R 5 \boldsymbol{x}_{1}=\left[\begin{array}{c}1 \\2 \\-1 \\-1 \\-1\end{array}\right], \quad \boldsymbol{x}_{2}=\left[\begin{array}{c}2 \\-1 \\1 \\2 \\-2\end{array}\right], \quad \boldsymbol{x}_{3}=\left[\begin{array}{c}3 \\-4 \\3 \\5 \\-3\end{array}\right], \quad \boldsymbol{x}_{4}=\left[\begin{array}{c}-1 \\8 \\-5 \\-6 \\1\end{array}\right] \in \mathbb{R}^{5} x1=⎣⎢⎢⎢⎢⎡12−1−1−1⎦⎥⎥⎥⎥⎤,x2=⎣⎢⎢⎢⎢⎡2−112−2⎦⎥⎥⎥⎥⎤,x3=⎣⎢⎢⎢⎢⎡3−435−3⎦⎥⎥⎥⎥⎤,x4=⎣⎢⎢⎢⎢⎡−18−5−61⎦⎥⎥⎥⎥⎤∈R5
我们关注 x 1 , … , x 4 \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{4} x1,…,x4中哪几个是 U U U的基。为此,我们需要判断 x 1 , … , x 4 \boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{4} x1,…,x4是否线性独立。因此,我们需要解一个矩阵齐次方程组:
∑ i = 1 4 λ i x i = 0 \sum_{i=1}^{4} \lambda_{i} \boldsymbol{x}_{i}=\mathbf{0} i=1∑4λixi=0
对应矩阵为:
[ x 1 , x 2 , x 3 , x 4 ] = [ 1 2 3 − 1 2 − 1 − 4 8 − 1 1 3 − 5 − 1 2 5 − 6 − 1 − 2 − 3 1 ] \left[\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \boldsymbol{x}_{3}, \boldsymbol{x}_{4}\right]=\left[\begin{array}{cccc}1 & 2 & 3 & -1 \\2 & -1 & -4 & 8 \\-1 & 1 & 3 & -5 \\-1 & 2 & 5 & -6 \\-1 & -2 & -3 & 1\end{array}\right] [x1,x2,x3,x4]=⎣⎢⎢⎢⎢⎡12−1−1−12−112−23−435−3−18−5−61⎦⎥⎥⎥⎥⎤
利用线性方程组的基本变换规则,得到了行阶梯型矩阵:
[ 1 2 3 − 1 2 − 1 − 4 8 − 1 1 3 − 5 − 1 2 5 − 6 − 1 − 2 − 3 1 ] ⇝ ⋯ ⇝ [ 1 2 3 − 1 0 1 2 − 2 0 0 0 1 0 0 0 0 0 0 0 0 ] \left[\begin{array}{rrrr}1 & 2 & 3 & -1 \\2 & -1 & -4 & 8 \\-1 & 1 & 3 & -5 \\-1 & 2 & 5 & -6 \\-1 & -2 & -3 & 1\end{array}\right] \quad \rightsquigarrow \cdots \rightsquigarrow \quad\left[\begin{array}{cccc}1 & 2 & 3 & -1 \\0 & 1 & 2 & -2 \\0 & 0 & 0 & 1 \\0 & 0 & 0 & 0 \\0 & 0 & 0 & 0\end{array}\right] ⎣⎢⎢⎢⎢⎡12−1−1−12−112−23−435−3−18−5−61⎦⎥⎥⎥⎥⎤⇝⋯⇝⎣⎢⎢⎢⎢⎡100002100032000−1−2100⎦⎥⎥⎥⎥⎤
由于主元列对应的那组向量是线性独立的,因此我们从行阶梯型可以看出 x 1 , x 2 , x 4 \boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \boldsymbol{x}_{4} x1,x2,x4是线性独立的(因为线性方程组 λ 1 x 1 + λ 2 x 2 + λ 4 x 4 = 0 \lambda_{1} x_{1}+\lambda_{2} x_{2}+\lambda_{4} x_{4}=0 λ1x1+λ2x2+λ4x4=0只能用 λ 1 = λ 2 = λ 4 = 0 \lambda_{1}=\lambda_{2}=\lambda_{4}=0 λ1=λ2=λ4=0来解)。因此, { x 1 , x 2 , x 4 } \left\{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \boldsymbol{x}_{4}\right\} { x1,x2,x4}是 U U U的基。
2.6.2 秩
矩阵 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n的线性独立列的个数等于线性独立行的个数,这个数称为 A \boldsymbol{A} A的秩(Rank),用 rk ( A ) \operatorname{rk}(\boldsymbol{A}) rk(A)表示。
备注:
矩阵的秩有一些重要的性质:
- rk ( A ) = rk ( A ⊤ ) \operatorname{rk}(\boldsymbol{A})=\operatorname{rk}\left(\boldsymbol{A}^{\top}\right) rk(A)=rk(A⊤),即列秩等于行秩
- A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n的列张成一个子空间 U ⊆ R m U \subseteq \mathbb{R}^{m} U⊆Rm, dim ( U ) = rk ( A ) \operatorname{dim}(U)=\operatorname{rk}(\boldsymbol{A}) dim(U)=rk(A)。在后面内容中我们将这个子空间称为像或值域。通过对 A \boldsymbol{A} A应用高斯消元法来确认主元列,可以找到 U U U的基。
- A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n的行张成一个子空间 W ⊆ R n W \subseteq \mathbb{R}^{n} W⊆Rn, dim ( W ) = rk ( A ) \operatorname{dim}(W)=\operatorname{rk}(\boldsymbol{A}) dim(W)=rk(A)。通过对 A ⊤ \boldsymbol{A}^{\top} A⊤应用高斯消元法来确认主元列,可以找到 W W W的基。
- 对于任意方阵 A ∈ R n × n \boldsymbol{A} \in \mathbb{R}^{n \times n} A∈Rn×n, A \boldsymbol{A} A是正则的(可逆)当且仅当 rk ( A ) = n \operatorname{rk}(\boldsymbol{A})=n rk(A)=n
- 对于任意 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n,和 b ∈ R m \boldsymbol{b} \in \mathbb{R}^{m} b∈Rm,线性方程组 A x = b \boldsymbol{A}\boldsymbol{x}=\boldsymbol{b} Ax=b有解当且仅当 rk ( A ) = rk ( A ∣ b ) \operatorname{rk}(\boldsymbol{A})=\operatorname{rk}(\boldsymbol{A} \mid \boldsymbol{b}) rk(A)=rk(A∣b),其中 A ∣ b \boldsymbol{A} \mid \boldsymbol{b} A∣b表示增广矩阵。
- 对于任意 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n, A x = 0 \boldsymbol{A}\boldsymbol{x}=\boldsymbol{0} Ax=0的解的子空间维数为 n − rk ( A ) n-\operatorname{rk}(\boldsymbol{A}) n−rk(A)。后面我们会称这个子空间为核或零空间。
- 如果矩阵 A ∈ R m × n \boldsymbol{A} \in \mathbb{R}^{m \times n} A∈Rm×n的秩等于相同维数矩阵的最大可能秩,则它拥有满秩( full rank)。也就是说满秩矩阵的秩是行数和列数中的较小者,即 rk ( A ) = min ( m , n ) \operatorname{rk}(\boldsymbol{A})=\min (m, n) rk(A)=min(m,n)。如果矩阵不满足满秩的要求,则称它不满秩( rank deficient)。
例 2.18
-
A = [ 1 0 1 0 1 1 0 0 0 ] \boldsymbol{A}=\left[\begin{array}{lll}1 & 0 & 1 \\0 & 1 & 1 \\0 & 0 & 0\end{array}\right] A=⎣⎡100010110⎦⎤
A \boldsymbol{A} A有两个线性独立的行/列,所以 rk ( A ) = 2 \operatorname{rk}(\boldsymbol{A})=2 rk(A)=2 -
A = [ 1 2 1 − 2 − 3 1 3 5 0 ] \boldsymbol{A}=\left[\begin{array}{ccc}1 & 2 & 1 \\-2 & -3 & 1 \\3 & 5 & 0\end{array}\right] A=⎣⎡1−232−35110⎦⎤
使用高斯消元法来确定秩:
[ 1 2 1 − 2 − 3 1 3 5 0 ] ⇝ ⋯ ⇝ [ 1 2 1 0 1 3 0 0 0 ] \left[\begin{array}{ccc}1 & 2 & 1 \\-2 & -3 & 1 \\3 & 5 & 0\end{array}\right] \quad \rightsquigarrow \cdots \rightsquigarrow \quad\left[\begin{array}{ccc}1 & 2 & 1 \\0 & 1 & 3 \\0 & 0 & 0\end{array}\right] ⎣⎡1−232−35110⎦⎤⇝⋯⇝⎣⎡100210130⎦⎤
有两个线性独立的行/列,所以 rk ( A ) = 2 \operatorname{rk}(\boldsymbol{A})=2 rk(A)=2
翻译自:
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth,A Aldo Faisal 和 Cheng Soon Ong
公众号后台回复【m4ml】即可获取这本书。
另外,机器学习的数学基础.pdf