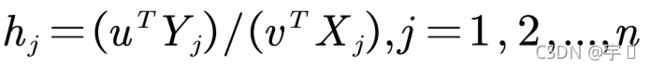数据包络分析(DEA)详解(以第八届宁夏省赛为例)
目录
一、基本介绍
1.1原理
1.2CCR模型
1.3BCC模型
二、代码
2.1MATLAB代码
2.2Python代码
三、案例分析
3.1案例介绍
3.2案例分析
3.3案例求解
一、基本介绍
1.1原理
数据包络分析有多种模型,主要为:CCR模型,BBC模型、交叉模型、A&P模型。纵观该方法的各种模型,每一模型的具体数学推理过程基本一致,所得的标准线性规划求解公式也比较相似,它们之间的差异主要体现在每个模型所适用的条件有所不同。在国外,此方法较早地运用于银行医院、城市等方面效率的评价。近些年来,该方法在我国社会经济的许多领域也取得了不少应用成果。由于方法对评价对象的要求相对比较宽松,应用其评价相同类型DMU的相对有效性的优势地位,是其他方法难以取代的。
1.2CCR模型
CCR模型是指对DMU通过“投入一定数量的生产要素,并产出一定数量的产品”的经济系统来判断各个单元的相对合理性和有效性。从投入资源的角度来看,在当前产出的水准下,比较投入资源的使用情况,以此作为效益评价的依据,这种模式称为“投入导向模式”。
定义决策单元j的效率评价指数为:
对上式可以适当的取权系数v和u,使得![]() ,对第
,对第![]() 个决策单元进行效率评价,一般来说
个决策单元进行效率评价,一般来说![]() 越大表明
越大表明![]() 能够用相对较少的输入而取得相对较多的输出。故只需求得的最大值,即可探究
能够用相对较少的输入而取得相对较多的输出。故只需求得的最大值,即可探究![]() 在这n个DUM中相对来说是不是最优的。
在这n个DUM中相对来说是不是最优的。
1.3BCC模型
BCC模型是从产出的角度探讨效率,即在相同的投入水准下,比较产出资源的达成情况,这种模式称为“投入导向模式”。所得到的是“技术效益”,DEA=1称为“技术有效”,最优解![]() 是决策单元j的“技术效益”。
是决策单元j的“技术效益”。
二、代码
2.1MATLAB代码
clear
clc
format long
data=[14.40 0.65 31.30 3621.00 0.00
16.90 0.72 32.20 3943.00 0.09
15.53 0.72 31.87 4086.67 0.07
15.40 0.76 32.23 4904.67 0.13
14.17 0.76 32.40 6311.67 0.37
13.33 0.69 30.77 8173.33 0.59
12.83 0.61 29.23 10236.00 0.51
13.00 0.63 28.20 12094.33 0.44
13.40 0.75 28.80 13603.33 0.58
14.00 0.84 29.10 14841.00 1.00]';
X=data([1:3],:);%X为输入变量
Y=data([4:5],:);%Y为输出变量
[m,n]=size(X);
s=size(Y,1);
A=[-X' Y'];%由于目标函数求最小,这里的-X就转化成了求最大
b=zeros(n,1);
LB=zeros(m+s,1);UB=[];
for i=1:n
f=[zeros(1,m) -Y(:,i)'];
Aeq=[X(:,i)',zeros(1,s)];
beq=1;
w(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);%前3列为投入系数,后2列为产出系数
E(i,i)=Y(:,i)'*w(m+1:m+s,i);%产出值*产出系数
end
theta=diag(E)';
fprintf('用DEA方法对此的相对评价结果为:\n');
disp(theta);2.2Python代码
import gurobipy
import pandas as pd
# 分页显示数据, 设置为 False 不允许分页
pd.set_option('display.expand_frame_repr', False)
# 最多显示的列数, 设置为 None 显示全部列
pd.set_option('display.max_columns', None)
# 最多显示的行数, 设置为 None 显示全部行
pd.set_option('display.max_rows', None)
class DEA(object):
def __init__(self, DMUs_Name, X, Y, AP=False):
self.m1, self.m1_name, self.m2, self.m2_name, self.AP = X.shape[1], X.columns.tolist(), Y.shape[1], Y.columns.tolist(), AP
self.DMUs, self.X, self.Y = gurobipy.multidict({DMU: [X.loc[DMU].tolist(), Y.loc[DMU].tolist()] for DMU in DMUs_Name})
print(f'DEA(AP={AP}) MODEL RUNING...')
def __CCR(self):
for k in self.DMUs:
MODEL = gurobipy.Model()
OE, lambdas, s_negitive, s_positive = MODEL.addVar(), MODEL.addVars(self.DMUs), MODEL.addVars(self.m1), MODEL.addVars(self.m2)
MODEL.update()
MODEL.setObjectiveN(OE, index=0, priority=1)
MODEL.setObjectiveN(-(sum(s_negitive) + sum(s_positive)), index=1, priority=0)
MODEL.addConstrs(gurobipy.quicksum(lambdas[i] * self.X[i][j] for i in self.DMUs if i != k or not self.AP) + s_negitive[j] == OE * self.X[k][j] for j in range(self.m1))
MODEL.addConstrs(gurobipy.quicksum(lambdas[i] * self.Y[i][j] for i in self.DMUs if i != k or not self.AP) - s_positive[j] == self.Y[k][j] for j in range(self.m2))
MODEL.setParam('OutputFlag', 0)
MODEL.optimize()
self.Result.at[k, ('效益分析', '综合技术效益(CCR)')] = MODEL.objVal
self.Result.at[k, ('规模报酬分析', '有效性')] = '非 DEA 有效' if MODEL.objVal < 1 else 'DEA 弱有效' if s_negitive.sum().getValue() + s_positive.sum().getValue() else 'DEA 强有效'
self.Result.at[k, ('规模报酬分析', '类型')] = '规模报酬固定' if lambdas.sum().getValue() == 1 else '规模报酬递增' if lambdas.sum().getValue() < 1 else '规模报酬递减'
for m in range(self.m1):
self.Result.at[k, ('差额变数分析', f'{self.m1_name[m]}')] = s_negitive[m].X
self.Result.at[k, ('投入冗余率', f'{self.m1_name[m]}')] = 'N/A' if self.X[k][m] == 0 else s_negitive[m].X / self.X[k][m]
for m in range(self.m2):
self.Result.at[k, ('差额变数分析', f'{self.m2_name[m]}')] = s_positive[m].X
self.Result.at[k, ('产出不足率', f'{self.m2_name[m]}')] = 'N/A' if self.Y[k][m] == 0 else s_positive[m].X / self.Y[k][m]
return self.Result
def __BCC(self):
for k in self.DMUs:
MODEL = gurobipy.Model()
TE, lambdas = MODEL.addVar(), MODEL.addVars(self.DMUs)
MODEL.update()
MODEL.setObjective(TE, sense=gurobipy.GRB.MINIMIZE)
MODEL.addConstrs(gurobipy.quicksum(lambdas[i] * self.X[i][j] for i in self.DMUs if i != k or not self.AP) <= TE * self.X[k][j] for j in range(self.m1))
MODEL.addConstrs(gurobipy.quicksum(lambdas[i] * self.Y[i][j] for i in self.DMUs if i != k or not self.AP) >= self.Y[k][j] for j in range(self.m2))
MODEL.addConstr(gurobipy.quicksum(lambdas[i] for i in self.DMUs if i != k or not self.AP) == 1)
MODEL.setParam('OutputFlag', 0)
MODEL.optimize()
self.Result.at[k, ('效益分析', '技术效益(BCC)')] = MODEL.objVal if MODEL.status == gurobipy.GRB.Status.OPTIMAL else 'N/A'
return self.Result
def dea(self):
columns_Page = ['效益分析'] * 3 + ['规模报酬分析'] * 2 + ['差额变数分析'] * (self.m1 + self.m2) + ['投入冗余率'] * self.m1 + ['产出不足率'] * self.m2
columns_Group = ['技术效益(BCC)', '规模效益(CCR/BCC)', '综合技术效益(CCR)','有效性', '类型'] + (self.m1_name + self.m2_name) * 2
self.Result = pd.DataFrame(index=self.DMUs, columns=[columns_Page, columns_Group])
self.__CCR()
self.__BCC()
self.Result.loc[:, ('效益分析', '规模效益(CCR/BCC)')] = self.Result.loc[:, ('效益分析', '综合技术效益(CCR)')] / self.Result.loc[:,('效益分析', '技术效益(BCC)')]
return self.Result
def analysis(self, file_name=None):
Result = self.dea()
file_name = 'DEA 数据包络分析报告.xlsx' if file_name is None else f'\\{file_name}.xlsx'
Result.to_excel(file_name, 'DEA 数据包络分析报告')
三、案例分析
3.1案例介绍
3.2案例分析
问题一首先要求我们对原始数据进行分析并预处理,在种类繁多的各项指标中,找到合适的投入与产出指标,构建评价体系,建立数学模型,找到对机构运营效率影响较大的关键内部指标,计算各妇幼保健机构在各分项指标及总体运营效率得分。很明显,这是一个多指标投入和多指标产出对相同类型的单位(部门)进行相对有效性或效益评价的系统分析问题,我们查阅大量文献之后选择利用数据包络分析(DEA)方法来解决该问题。
在对数据进行DEA分析之前我们要对数据进行预处理,首先对原始数据给出的各项指标进行分类,找到他们的二级指标甚至一级指标,从而划分投入指标和产出指标,之后利用Excel和Python将数据集中的错误数据进行清理,在查阅大量文献的基础上,剔除相对不重要的指标,创造出新的数据集,导入MPai数据科学平台,首先对每一年的数据集分别进行DEA分析,最后再计算技术效益、规模效益、综合技术效益的算术均值,即可解决该问题。
相对于问题一,问题二更符合实际情况,研究价值更高,毕竟研究医院管理离不开卫生经济,研究卫生经济离不开国家宏观经济,妇幼保健机构所在地区经济发展水平、人口等客观因素对其发展程度和运行效率的影响是巨大的。当前,我国宏观经济形势进入新常态,下行压力非常大。同时,人口老龄化程度加重,由于缺乏劳动力,对整个经济的发展是不利的,经济问题本质上就是人口问题,整个经济下滑了,对医疗卫生的投入就难以增加,医院的收入就难以增长,只能实行严格的医疗控费。因此,探索不同投入结构变化对最终运营效率的影响刻不容缓。
在问题一的基础上,我们首先访问各省的统计年鉴,获取相应省份医疗卫生费用占GDP的比重以及各省对于妇幼保健机构的支持程度,查阅大量文献,确定影响因子,利用优劣解距离法(TOPSIS)消除量纲的影响,对各个妇幼保健机构进行综合得分评价,从而找到不同投入结构变化对最终运营效率的影响。
通过对问题一和问题二的分析求解,我们了解到某些妇幼保健机构运行效率较低,存在明显的医疗卫生资源浪费的情况,针对于此,我们将在自身研究结果的基础上,致信相应的妇幼保健机构管理者,用报告的形式将他们暴露出来的问题直观的展现到他们面前,并给出针对性的意见,帮助他们更快、更好的解决自身资源使用,提高运行效率,充分使用医疗卫生资源。
3.3案例求解
差额变数分析是基于松弛变量(差额变数、超额变数)的分析,根据冗余情况进行适当减少投入冗余、增加产出不足上表展示了差额变数分析投入与产出的部分/全部的增减量,2020年各妇幼保健机构差额变数分析结果如下表3所示。差额变数:指为达到目标效率可以减少的投入量,即非DEA有效单元的实际值和目标值之差,超额变数:指为达到目标效率可以增加的产出量,即非DEA有效地区的目标值和实际值之差。
在学习中成功、在学习中进步!我们一起学习不放弃~
记得三连哦~ 你们的支持是我最大的动力!!欢迎大家阅读往期文章哈~
小编联系方式如下,欢迎各位巨佬沟通交流。
print("QQ:1654243128")![]()