超详细的c进阶教程（一）！C语言数据存储剖析

作者的码云地址：https://gitee.com/dongtiao-xiewei
后续作者会更新力扣的每日一题系列，原代码会全部上传码云，推荐关注哦，笔芯~

还像更深入地了解c语言？快来订阅作者的c语言进阶专栏！作者承诺本系列不会TJ！预计更新：指针，字符串处理，内存管理，结构体，预处理等等

课后作业解析地址：

冲鸭冲鸭！今天为大家详细介绍一下数据类型在内存中的处理和存储方式

数据类型简介

更详细的介绍可以参考我的另外一篇文章c语言数据类型入门系列
程序离不开数据，我们把数字，字母等数字写入计算机，就是希望计算机帮助我们进行一系列复杂的运算，而在c语言中，数据类型大致分为以下几种

整型	浮点型
短整型（short）	单精度型（float）
整型（int）	双精度型（double）
长整型（long）	长精度浮点类型（long double）
字符类型（char）

以及还有无符号的整型：unsigned int,unsigned long 等
计算机为什么会分为这么多种的数据类型呢？

1. 我们要知道，计算机在存储数据时，不是像我们人脑一样，整数，分数，字符都能完全区分
2. 计算机在存储数据的时候全是使用二进制存储的，所以我们需要让计算机学会如何将这些二进制信息转化成我们需要处理的信息，如整数，分数等
3. 计算机将这些数据分类存储起来，方便表示出各种各样的数据以及分类计算

那么类型的意义可以在计算机那些方面体现出来呢？
答案是在内存方面，其实每个数据类型在计算机中占用的字节大小是不一样的

数据类型在内存层面的意义

小科普

1字节(byte)对应计算机中为8个bit位(表示为0000 0000),换算为16进制1字节为两位

---

数据类型	内存占用大小
char	1byte
short	2byte
int	4byte
long	4byte
long long	8byte
float	4byte
double	8byte

不同的数据类型占用不同大小
数据类型决定了内存数据的使用范围

我们来举一个栗子

int main()
{
     
	//比如我们希望通过一个指针变量修改整型变量a的值
	int a = 0x11223344;//这里使用了十六进制表示法，方便观察
	char* p = &a;//我们定义一个char*变量来尝试修改a，看看能不能达到期望的修改效果
	*p = 0;
	

	return 0;
}

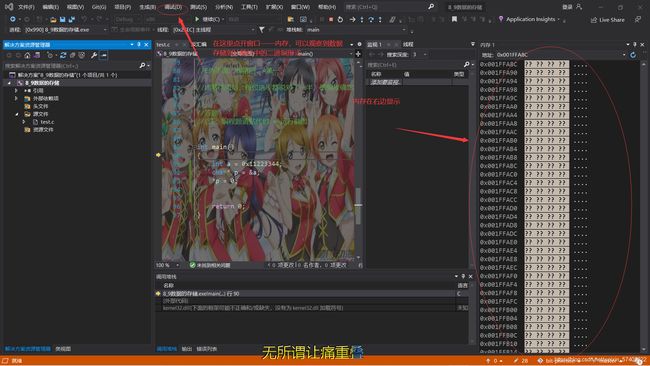
我们使用的是VS2019进行调试，按F10可以进行调试，在调试过程中可以查看内存情况

我们取出a的地址放在右边观察a的变化

调试到程序的末尾，可以观察到a的改变情况

为什么这里a只改变了4个字节呢？

数据类型的意义就体现出来了
int占用4个字节，所以内存中为a变量分配了4的字节的空间来存储，而char大小仅为1个字节，它的存储和修改权限仅为一个字节

介绍完数据类型，那么计算机的数据储存和计算怎么在电脑里面进行呢？

整型数据在计算机中存储和处理

拿int类型举例，int类型有4个字节，就拥有4*8=32个比特位，其中最高位用于存放正负情况，0为正，1为负0.其它位存放将int类型转化为2进制的信息

符号位	数据位
0或1	000 0000 0000 0000 0000 0000 0000 0000

例如-1的原码可以表示为1 000 0000 0000 0000 0000 0000 0000 0001

-1为为负数，所以将符号位设为1
1转换为二进制就是1，不足的位数直接补0

原码，反码和补码

为什么会出现这三种编码方式？
这要从CPU说起
我们知道，CPU是不会进行减法运算的

比如说要计算1-1的结果，计算机只会把它处理成1+（-1）

1的原码为：0000 0000 0000 0000 0000 0000 0000 0001
-1的原码为：1000 0000 0000 0000 0000 0000 0000 0001
所以计算机会将1-1视为1+（-1）进行运算
结果为1000 0000 0000 0000 0000 0000 0000 0010
但是1-1的十进制结果是-2，这显然不对

所以我们为了能将正数负数统一进行运算，引入了这三种编码方式

就要用到原码反码补码了~
先甩出结论叭

---

1. 正数的原码，反码，补码相同
2. 负数的转换方式

• 原码：参考本节开头，符号位，其它位
• 将原码的符号位不动，其它位按位取反，可得到反码
• 反码+1得到补码

3. 计算机通过补码存储和运算数据
4. 在打印数据时需要将补码翻译成原码

例如：

1为正数，原码，反码，补码相同
都为0000 0000 0000 0000 0000 0000 0000 0001
-1为负数
原码为：1000 0000 0000 0000 0000 0000 0000 0001
反码为：1111 1111 1111 1111 1111 1111 1111 1110
//除了符号位，其它按位取反
补码为：1111 1111 1111 1111 1111 1111 1111 1111
//反码+1

这样运算就不会出现问题了
就能实现计算机中将正负数统一标准进行计算的功能，不需要额外的硬件

补充一下截断现象：如果某个数字转化为二进制的字节数超过了类型大小，将会在左边将多出的数据舍弃，保存右边未舍弃的部分
讲完这些，可能大家都好奇计算机储存数据的体现，那么现在开始调试，看看数据在计算机中的存储情况吧

int a=10000;

将上述16进制数字（f0 d8 ff ff）翻译成二进制结果是：
唉不对，先不忙这样翻译，我们先讲一下大小端的问题吧~

大端和小端存储方式

什么是大端小端？

• 大端：数据的低位保存在内存的高地址中，高位保存在低地址
• 小端：数据的高位保存在内存的高地址中，低位保存在低地址

我们先拿个简单的数字举个栗子吧

int a=1;

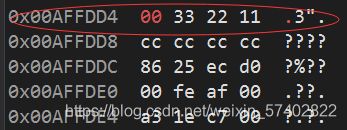
我们可以观察出：
01明明是在数据的末尾，为啥还在内存的最前面两位显示
其实在计算机中，在高位显示的却是代表的低地址

1转化为2进制是0000 0001
我们可以得出结论：此数据使用小端模式存储
作者用的VS2019,VS2019使用小端模式存储

所以我们翻译上面的10000的时候，需要反起来翻译哦！

---

为什么会有大小端之分呢？
因为在计算机系统中，我们是以字节为单位的，每个地址单元对应1字节，而为了储存超过1字节的数据的时候，就存在每个字节存放顺序的问题

---

我们在处理数据的时候，一般都是相同数据之间进行处理，但是也有意外情况，如果我们希望处理两个类型不同的数据，又该怎么样处理呢？

整型提升和算术转换

整型提升

在计算机中计算数据的话，整型运算要在CPU相应运算器件内运行。
而CPU内整型运算器的字节长度就是4个字节，也就是一个int类型的长度。

因此，针对char和short等不足4字节的整型数据进行计算，需要将它们先转化为4字节大小的普通整型进行计算

计算完毕后，保存仍会保存原来数据类型大小的数据

这里举一个栗子：

int main()
{
     
	char a = 3;//0000 0011
	char b = 127;//0111 1111
	char c = a + b;
	printf("%d\n", c);
	return 0;
}

输出结果是

在实际进行计算是以下这样的

运算完后因为c是char类型，所以又将不属于char的部分截断

所以我们的运算结果是-126

结论：整型提升方式为用原数据符号位补齐
无符号数据类型，补充0

整型提升在运算中发生

char c=1;
printf("%u\n",sizeof(+c));
//输出结果为4，因为+c相当于一次运算，c会提升至int类型

算术转换

由下到上依次为

long double
double
float
unsigned long
long
unsigned
int

计算时，位于下面的类型会转化为上面的数据类型进行计算

关于无符号整型的一些性质

1. 无符号整型会无视符号位，将最高位也视作数据位，所以它用于存储数据的比特位比有符号整型多1范围也更大。例如：char的范围为-127–128，无符号char范围为0–255
2. 将负数转换为无符号型，会直接将其补码翻译成某个正数对应的补码，而正数的原码又等于补码。

• 例如-1的补码为 1111 1111 1111 1111 1111 1111 1111 1111，将其转换为无符号整型，会直接将其补码翻译成某个正数，这个数将会很大，大约在42亿。

总之：将一个负数翻译成无符号整型，不需要将其翻译成原码，只需要将其对应二进制（包括符号位）翻译成对应10进制就行了

整数就差不多讲完了，接下来讲讲浮点数

---

浮点型数据在计算机中存储和处理

浮点型也体现在它的存储方式和整型不一样

浮点型转换为二进制

从小数点第n位开始，依次乘以2的-n次方
例如0.5
因为2^-1=0.5
所以转化写成0.1

IEEE标准（754）

任意一个二进制数可以表示为以下的形式

(-1)^s * M * 2^E
其中s代表符号位，s=0为正，1为负
M代表有效数字的信息，1<=M<2
E代表指数位

一个栗子：
5.5转化为二进制为101.1

1. 正数，符号位S为0
2. 将其转为科学计数法为1.011*10²，所以指数位E为2
3. 有效数字M即为1.011

浮点型数据的存储

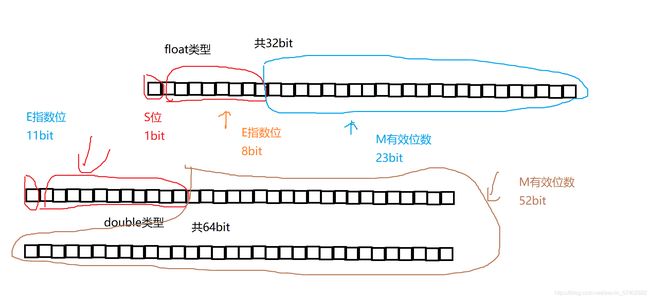
单精度和双精度型

我们可以尝试调试观察一下5.5的存储情况

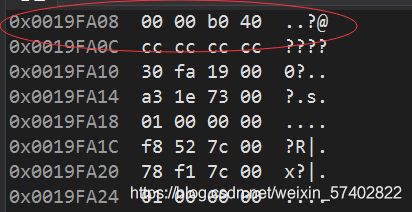
float f=5.5

翻译成二进制就是

0 10000001 011 0000 0000 0000 0000 0000

位数不足的自动补0,但是指数好像又有点不对？

指数E

E在标准中被定义为无符号整型，但是在实际运算中可能会出现0.0023这样的数字，它的指数位数小于0，所以标准对于E会进行修正

指数的十进制形式加上一个中间值再进行存储
32位加上127，64位加上1023

例如0.5，二进制表示为2^-1,其指数存储需要存储为-1+127=126的二进制形式

总结与提示

1. 数据类型的意义：决定使用空间的大小，丰富了计算机储存数据的种类
2. 数据在内存中的存储和运算需要遵守一定的规则，例如原反补码，整形提升等。
3. 牢记浮点型类型的存储标准

巩固

• 以下程序的输出结果是？

//1.
char a=-128;
printf("%u\n",a);
//2.
unsigned int i;
for(i=9;i>=0;i--)
{
     
	printf("%u\n",i);
}
//3.
char a[1000];
int i;
for(i=0;i<1000;i++)
{
     
	a[i]=-1-i;
}
printf("%d\n",strlen(a));

• 请你设计一种程序，验证该机器数据存储是采用小端存储还是大端存储

本期内容到此结束啦！由于作者水平有限，文章中如有不足与疏漏之处在所难免，希望各位大佬提出你们宝贵的意见！笔芯~