鲸鱼算法优化变分模态分解(VMD)包络熵和参数的特征提取及MATLAB代码实现
目录
1 简介
2 变分模态分解VMD原理
3 鲸鱼优化算法优化VMD原理
3.1. 鲸鱼优化算法优化VMD原理及流程
3.2. 特征提取流程
4 优化效果
4.1. VMD各分量信号时域图
4.2. 鲸鱼优化算法优化VMD各分量信号时域图
4.3 全部图像
5. 主要代码
main.m
woa_vmd.m
1 简介
针对从滚动轴承振动信号中所提取的故障信息精度低的问题,利用鲸鱼优化算法对变分模态分解模态个数K和惩罚参数α 寻优,然后根据VMD处理信号得到若干模态分量,筛选后进一步提取能量熵作为特征向量。使用特征提取向量,可进行后续轴承故障诊断等工作。
2 变分模态分解VMD原理
VMD能够自适应匹配每种模态的最佳中心频率和有限带宽,实现固有模态分量(IMF)有效分离,
其核心思想是构建和求解变分问题。
VMD实现步骤为:
由VMD分解步骤可知,分解信号前需要设置合适的模态个数K和惩罚参数α,K取值过大会导致过分解,反之,则会欠分解,α 取值过大,会造成频带信息丢失,反之,会信息冗余,所以需要确定最佳参数组合[K,α]。目前多用中心频率观察法,通过观察不同K值下的中心频率确定K值,但该法具有偶然性,且只能确定模态个数K,无法确定惩罚参数α。
3 鲸鱼优化算法优化VMD原理
3.1. 鲸鱼优化算法优化VMD原理及流程
使用鲸鱼优化算法(WOA)对VMD参数进行寻优,以包络熵极小值作为适应度函数,包络熵代表原始信号的稀疏特性,当IMF中噪声较多,特征信息较少时,则包络熵值较大,反之,则包络熵值较小。
信号x (i )(i = 1,2,…,N )包络熵EP 用以下公式计算,式中a (i ) 是由VMD 分解的k 个模态分量经Hilbert 解调后的包络信号,ε (i )是通过计算a (i )的归一化得到的概率分布序列,N 为采样点数,计算概率分布序列ε (i )的熵值即为包络熵EP。
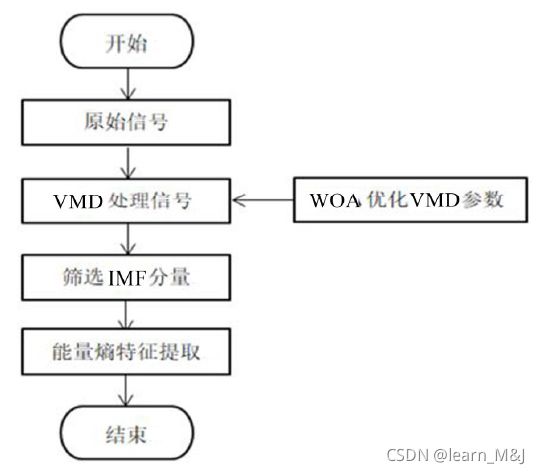
采用WOA优化VMD参数流程如图所示。首先初始化鲸群位置向量[K,α],以包络熵作为适应度函数,并计算每个鲸鱼适应度,然后通过判断收敛因子大小选择迭代公式进行迭代更新,直到满足终止条件,输出最优VMD参数。
3.2. 特征提取流程
VMD 利用WOA寻优后的参数组合[K,α]采用VMD对原信号分解,得到K个模态分量,计算每个IMF 峭度值,将其定义为:
式中:μ为信号x 的均值,σ 为信号x 的标准差。
4 优化效果
4.1. VMD各分量信号时域图
4.2. 鲸鱼优化算法优化VMD各分量信号时域图
4.3 全部图像
5. 主要代码
main.m
%% 基于鲸鱼优化算法(whale optimization algorithm, WOA)优化变分模态分解(variational mode decomposition,VMD)参数
clc
clear
close all
warning off
addpath('toolf')
% 读取数据
[file,path,indx] = uigetfile({'*.xlsx';'*.xls';'*.txt';'*.*'},'File Selector');
if indx == 1||indx==2
data=xlsread(strcat(path, file));
elseif indx == 3
data=load(strcat(path, file));
else
warning('请选择数据集进行实验');
return;
end
%采样频率
fs=12800;
% 读取前1000长度的信号
len=1000;
s=data(1:len);
% 采样时间
t = (0:len-1)/fs;
%% 设定鲸鱼优化算法参数
popsize =20; % 种群大小
iter = 30; % 最大迭代次数
dim = 2; % 变量个数
lb = [100 3]; % alpha范围 K范围 下限
ub = [2000 7]; % 上限
%% 鲸鱼优化算法WOA优化VMD参数
tic , % 开始计时
WOA_VMD(popsize,iter,dim,lb,ub,0); % 0表示不保存IMF,1,导出IMF并保存
toc, % 结束计时
woa_vmd.m
function WOA_VMD(varargin)
% 子函数用于鲸鱼算法优化VMD的惩罚系数alpha和分解层数K
% initialize position vector and score for the leader,初始化位置向量和领导者得分
Leader_pos=zeros(1,dim);
Leader_score=inf; %change this to -inf for maximization problems,将此更改为-inf以获得最大化问题,Inf无穷大
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);%Positions,存放数个个体的多维位置。
Convergence_curve=zeros(1,Max_iteration);%Convergence_curve收敛曲线
gbest_array = zeros(Max_iteration,2); % 初始化最优参数数组
% Main loop
for T=1:Max_iteration
for i=1:size(Positions,1)%对每个个体一个一个检查是否越界
% Return back the search agents that go beyond the boundaries of
% the search space,返回超出搜索空间边界的搜索代理
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:) for maximization problem
Leader_score=fitness; % Update alpha
Leader_pos=Positions(i,:);
end
end
disp(['current iteration is: ',num2str(T), ', best fitness is: ', num2str(Leader_score)])
gbest_array(T,:) = Leader_pos;
a=2-T*((2)/Max_iteration); % a decreases linearly fron 2 to 0 in Eq. (2.3)
% a2 linearly dicreases from -1 to -2 to calculate t in Eq. (3.12)
a2=-1+T*((-1)/Max_iteration);
% Update the Position of search agents,参数更新
for i=1:size(Positions,1)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A=2*a*r1-a; % Eq. (2.3) in the paper
C=2*r2; % Eq. (2.4) in the paper
b=1; % parameters in Eq. (2.5)
l=(a2-1)*rand+1; % parameters in Eq. (2.5)
p = rand(); % p in Eq. (2.6)
for j=1:size(Positions,2)%对每一个个体地多维度进行循环运算
if p<0.5%收缩包围机制
if abs(A)>=1
rand_leader_index = floor(SearchAgents_no*rand()+1);%floor将 X 的每个元素四舍五入到小于或等于该元素的最接近整数
X_rand = Positions(rand_leader_index, :);
D_X_rand=abs(C*X_rand(j)-Positions(i,j)); % Eq. (2.7)
Positions(i,j)=X_rand(j)-A*D_X_rand; % Eq. (2.8)
elseif abs(A)<1
D_Leader=abs(C*Leader_pos(j)-Positions(i,j)); % Eq. (2.1)
Positions(i,j)=Leader_pos(j)-A*D_Leader; % Eq. (2.2)
end
elseif p>=0.5%螺旋更新位置
distance2Leader=abs(Leader_pos(j)-Positions(i,j));
% Eq. (2.5)
Positions(i,j)=distance2Leader*exp(b.*l).*cos(l.*2*pi)+Leader_pos(j);
end
end
end
Convergence_curve(T)=Leader_score;
end 参考文献:张萍,张文海,赵新贺,吴显腾,刘宁.WOA-VMD算法在轴承故障诊断中的应用[J].噪声与振动控制,2021,41(04):86-93+275.
代码地址为:
MATLAB代码地址https://mianbaoduo.com/o/bread/YZ2ck5py![]() https://mianbaoduo.com/o/bread/YZ2ck5py
https://mianbaoduo.com/o/bread/YZ2ck5py