图像处理——空间域和频率域部分图像增强学习

图像增强Image Enhancement：采用某种技术手段，改善图像的视觉效果，获奖图像转换成更适合人眼观察和机器分析、识别的形式，以便从图像中获取更有用的信息。¹

• 空间域图像增强：针对图像自身，以对图像的像素直接处理为基础的方法；
  点处理，模板处理；
• 频率域图像增强：以修改图像的傅里叶变换为基础的方法；
  高、低通滤波，同态滤波。

另外还有彩色图像的增强。

1.空间域图像增强

1.1基于灰度变换的图像增强

属于点处理技术，这部分内容参考之前的笔记点运算部分内容 ,有线性变换、幂次变换等。

1.2基于直方图处理的图像增强

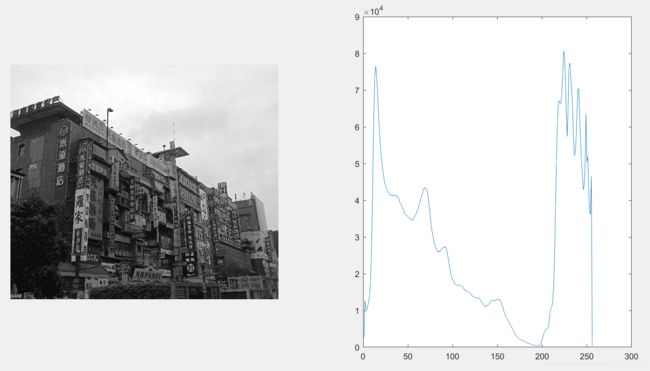
灰度级直方图统计了不同灰度级出现的概率。

I=imread('marketspace.jpg');
I=rgb2gray(I);
% I=double(uint8(I));
for i=1:256
    h(i)=sum(sum(I==i-1));
end
subplot(1,2,1);imshow(I);
subplot(1,2,2);plot(h);

直方图均衡化

直方图均衡化处理，使得图像的灰度分布趋向均匀，图像所占有的像素灰度间距拉开，进而加大图像反差，达到增强目的。适用于一些由于灰度分布集中在较窄区间内的图像。

I=imread('marketspace.jpg');
I=rgb2gray(I);
K=32;
H=histeq(I,K);
figure;
subplot(2,2,1);imshow(I);
subplot(2,2,2);imshow(H);hold on;
subplot(2,2,3),hist(double(I),16),
subplot(2,2,4),hist(double(H),16),

结果：

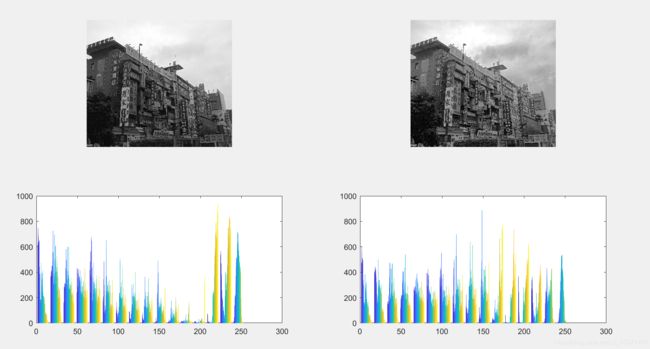
分析：
变换后直方图趋于平缓，灰级减少，灰度合并；原图像含像素多的几个灰级间隔被拉大，压缩的只是像素少的几个灰度级，实际视觉能接收的信息量增强了。可以看到增强的效果还是不错的，图中云层部分的细节有所增强。

1.3空间域滤波增强

属于模板处理技术，对图像进行滤波以去除图像噪声或增强图像细节。

空间域平滑滤波器

图像平滑（去噪）：抑制噪声、改善图像质量，通过积分使图像边缘模糊。

I=rgb2gray(imread('11.png'));
figure;
subplot(1,5,1),imshow(I),title("原始图像");
N=imnoise(I, 'salt & pepper', 0.06);
subplot(1,5,2),imshow(N),title("加椒盐噪声后的图像");
% 1）均值滤波
S=imfilter(N,fspecial('average', 5));
subplot(1,5,3),imshow(S),title("5*5领域平滑");
% 2）超限像素平滑法
T=20;
[m,n]=size(I);
C=zeros(m,n);
for i=1:m
    for j=1:n
        if abs(I(i, j)-S(i,j))>T
            C(i,j)=S(i,j);                      % if |I(x,y)-S(x,y)|>T then G(x,y)=S(x,y)
        else
            C(i,j)=I(i,j);                       % if |I(x,y)-S(x,y)|<=T then G(x,y)=I(x,y)
        end
    end
end
subplot(1,5,4),imshow(uint8(C));title("超限像素平滑法");
% 3）高斯平滑线性滤波法
G=imfilter(N, fspecial('gaussian', [3 3], 0.9), 'replicate');
subplot(1,5,5),imshow(G),title("高斯平滑滤波");

结果：

分析：
（1）超限像素平滑是对局部平滑法的一种改进，对抑制椒盐噪声比较有效，对保护仅有微小灰度差的细节及纹理也有效。
随着邻域增大，去噪能力增强，但模糊程度也增大。
（2）高斯滤波器，对于高斯噪声的去噪效果较好。

空间域锐化滤波器

图像锐化：增强图像的边缘和轮廓，通过微分使图像边缘清晰。

I=rgb2gray(imread('11.png'));
figure;
subplot(1,5,1),imshow(I),title("原始图像");
N=imnoise(I, 'salt & pepper', 0.02);
subplot(1,5,2),imshow(N),title("加椒盐噪声后的图像");
S=imfilter(N, fspecial('sobel'));
subplot(1,5,3), imshow(S),title("Sobel滤波");
L=imfilter(N, fspecial('laplacian', 0.2));
subplot(1,5,4),imshow(L),title("拉普拉斯滤波");
G=imfilter(N, fspecial('log', [5 5], 0.5));
subplot(1,5,5),imshow(G),title("高斯-拉普拉斯滤波");

结果：

2.频率域图像增强

频率域处理工作主要是：

$$g(x,y)=f(x,y)\ast h(x,y)$$

2.1频率域平滑滤波器

I=rgb2gray(imread('11.png'));
figure;
subplot(2,2,1),imshow(I),title("原始图像");
N=imnoise(I, 'salt & pepper', 0.02);
subplot(2,2,2),imshow(N),title("加椒盐噪声后的图像");
NF=fftshift(fft2(N));
[m,n]=size(N);
H=zeros(m,n);
% 1)理想低通滤波
T=105;
for i=1:m
    for j=1:n
        if sqrt((i-m/2)^2+(j-n/2)^2)<T
            H(i,j)=1;
        end
    end
end
L=NF.*H;
L=ifft2(ifftshift(L));
subplot(2,2,3),imshow(uint8(real(L))),title("理想低通滤波");
% 2）巴特沃斯低通滤波器
T=105;
N=2;
for i=1:m
    for j=1:n
        d=sqrt((i-m/2)^2+(j-n/2)^2);
        h=1/(1+(d/T)^(2*N));
        H(i,j)=h*NF(i,j);
    end
end
B=ifft2(ifftshift(H));
subplot(2,2,4),imshow(uint8(real(B))),title("巴特沃斯滤波");

结果（为了显示两种滤波器的效果区别，对图像进行了局部放大）：

分析：
（1）理想低通滤波器会产生振铃现象使图像变得模糊，相对而言，巴特沃斯滤波器没有陡峭的变化，图像边缘的模糊程度减小。
（2）阈值T越大，图像的模糊程度越低。

2.2频率域锐化滤波器

程序和上一个程序类似，只是公式稍有调整。

% 1)理想高通滤波
T=35;
for i=1:m
    for j=1:n
        if sqrt((i-m/2)^2+(j-n/2)^2)>T
            H(i,j)=1;
        end
    end
end
L=NF.*H;
L=ifft2(ifftshift(L));
subplot(2,2,3),imshow(uint8(real(L))),title("理想低通滤波");
% 2）巴特沃斯高通滤波器
T=35;
N=2;
for i=1:m
    for j=1:n
        d=sqrt((i-m/2)^2+(j-n/2)^2);
        h=1/(1+(T/d)^(2*N));
        H(i,j)=h*NF(i,j);
    end
end
B=ifft2(ifftshift(H));
subplot(2,2,4),imshow(uint8(real(B))),title("巴特沃斯滤波");

结果：

分析：
（1）巴特沃斯高通滤波器的效果较于理想高通滤波器好一点；
（2）阈值T的值越小，锐化程度越高。

2.3同态滤波器

同态滤波把频率滤波和灰度变换结合：

• 首先对非线性混杂信号做对数运算，把两个相乘的分量变为两个相加的分量，它们分别代表图像的高频和低频分量；
• 然后用线性滤波方法处理；
• 最后做逆运算，恢复处理后图像。

可以应用于消除光照不足带来的影响，同时又不损失图像细节。

I0=rgb2gray(imread('astronaut.jpg'));
I1=log(double(I0)+1);
I2=fft2(I1);
[m,n]=size(I2);
N=2;c=2;
T=7;
rh=2;rl=0.5;
for i=1:m
    for j=1:n
        d=sqrt(i^2+j^2);
        h=rl+(rh-rl)*(1/(1+(T/(c*d))^(2*N)));
        I2(i,j)=I2(i,j)*h;
    end
end
I3=ifft2(I2);
I4=(exp(I3)-1);
figure,
subplot(1,2,1),imshow(I0);
subplot(1,2,2),imshow(uint8(real(I4)));

结果：

分析：
（其实觉得这个结果没有很好，而且实验了很多照片，也没有找到效果好的）结果就是增强了图片的对比度，而且，阈值T越大，曝光度越小。

---

1. 出自杨杰主编的《数字图像处理及MATLAB实现（第2版）》 ↩︎