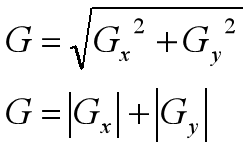opencv——Sobel算子与Scharr算子

算子

• 狭义的算子实际上是指从一个函数空间到另一个函数空间（或它自身）的映射。

• 广义的算子的定义只要把上面的空间推广到一般空间，可以是向量空间，赋范向量空间，内积空间，或更进一步，Banach空间，Hilbert空间都可以。算子还可分为有界的与无界的，线性的与非线性的等等类别。

边缘提取与梯度

如上图，在画圈处有明显的像素值变化，这就是图像中的边缘

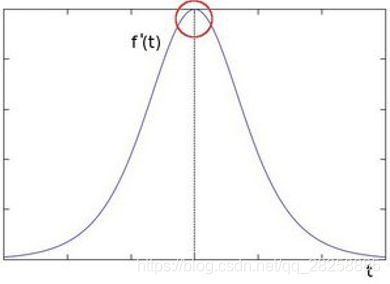
上图，是图像像素的变化图
圆圈处就是和源图像对应的点。可以看出，这里的变化率是最大的
变化率也称梯度
谈及变化率，我们就要想到导数
如下图

边缘提取

边缘是什么 – 像素值发生跃迁的地方
是图像的显著特征之一，在图像特征提取、对象检测、模式识别等方面都有重要的作用。

如何捕捉/提取边缘 – 对图像求它的一阶导数

  delta =  f(x) – f(x-1)

delta越大，说明像素在X方向变化越大，边缘信号越强

在opencv中，我们只需要使用Sobel算子就可以提取边缘，不用再使用求导操作

Sobel算子

原理

Sobel算子又叫索贝尔算子，是计算机视觉领域的一种重要处理方法。

主要用于获得数字图像的一阶梯度，常见的应用和物理意义是边缘检测。

Sobel算子是把图像中每个像素的上下左右四领域的灰度值加权差，在边缘处达到极值从而检测边缘。

Sobel算子所采用的算法是先进行加权平均，然后进行微分运算，算子的计算方法如下：

对于一个二元函数f(x,y)来说，x有三个取值，y有三个取值，那我们就可以构造一个3×3的矩阵，矩阵的中心点为（x,y），向上向左为减一，向右向下为加一。我们用矩阵来表示一下上面的式子：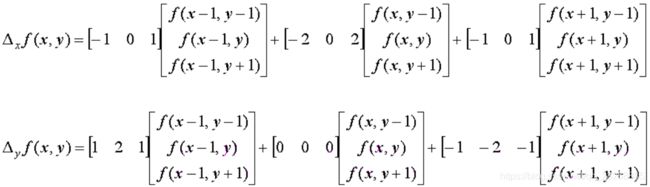
由此，我们设计两个核，一个是x方向上的，一个是y方向上的，设计的两个核是3×3的矩阵，分别是：

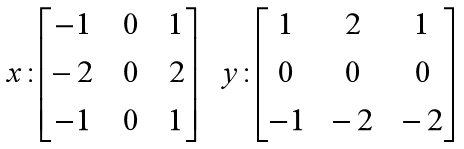
所以，如果对于一个图像I，我们能通过这两个核分别计算该图像X方向和Y方向的梯度：

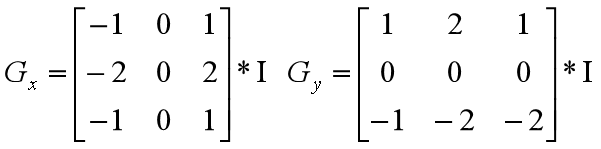
我们也能根据两个方向的梯度计算总的梯度：

第二个式子是第一个式子的近似计算，这是由于CPU乘除的开销远大于加减
所以会这么用

Sobel算子对噪声比较敏感，在使用前建议高斯模糊去噪再使用Sobel算子进行边缘提取

API

void Sobel( 
    InputArray src, 
    OutputArray dst, 
    int ddepth,  
    int dx,
    int dy,
    int ksize = 3,
    double scale = 1,                       
    double delta = 0, 
    int borderType = BORDER_DEFAULT 
);

• （1）InputArray类型的src ，输入图像。

• （2）OutputArray类型的dst ，输出图像，图像的大小、通道数和输入图像相同。

• （3）int类型的ddepth，输出图像深度，请参阅@ref filter_depth“组合”；如果是8位输入图像，则会导致导数截断。
  计算sobel的时候有负，一边黑一边白就变成500多了。如果我们的depth是-1，输入图像是CV_8U的灰度图像，输出也是CV_8U。那么超过255的就会被截断，与实际数值不吻合。所以输出图像的位数要比输入高，比如输入CV_8U，输出就要用CV_16S

• （4）int类型的dx，导数x的阶数。

• （5）int类型的dy，导数y的阶数。

• （6）int类型的ksize，扩展Sobel内核的大小；它必须是1、3、5或7。

• （7）double类型的scale，计算派生值的可选比例因子；默认情况下，不应用缩放（有关详细信息，请参见cv：：getDerivKernels。

• （8）double类型的delta，在将筛选的像素存储到dst中之前添加到这些像素的可选值。说的有点专业了其实就是给所选的像素值添加一个值delta。

• （9）int类型的borderType，用于推断图像外部像素的某种边界模式。有默认值BORDER_DEFAULT。

我们还用了一个很简单的函数，用于计算绝对值

void convertScaleAbs( 
    InputArray src, 
    OutputArray dst, 
    double alpha= 1,                       
    double belt= 0, 
);

我们这个函数只需要设置前两个参数，这个函数可以计算图像src的像素绝对值，输出到图像dst。

代码展示

#include
#include

using namespace std;
using namespace cv;

int main()
{
     
	Mat src, gx, gy, dst;

	src = imread("C:/Users/86176/Pictures/pics/lena(1).tiff");
	if (!src.data)
	{
     
		cout << "could not load image !";
		return -1;
	}
	imshow("【输入图像】", src);

	Mat tmp,gray;
	GaussianBlur(src, tmp, Size(3,3), 0, 0);
	cvtColor(tmp, gray, CV_BGR2GRAY);
	Sobel(gray, gx, CV_16S, 1, 0,3);
	Sobel(gray, gy, CV_16S, 0, 1,3);

	convertScaleAbs(gx, gx);
	convertScaleAbs(gy, gy);//若不用绝对值，那么产出的图像就会缺失很多细节
	addWeighted(gx, 0.5, gy, 0.5, 0, dst);

	imshow("【输出图像】", dst);

	waitKey(0);
	return 0;
}

结果

优化代码

我们在上述代码使用的是加权相加，并非是绝对值相加
我们现在来优化代码

#include
#include

using namespace std;
using namespace cv;

int main()
{
     
	Mat src, gx, gy, dst;

	src = imread("C:/Users/86176/Pictures/pics/lena(1).tiff");
	if (!src.data)
	{
     
		cout << "could not load image !";
		return -1;
	}
	imshow("【输入图像】", src);

	Mat tmp,gray;
	GaussianBlur(src, tmp, Size(3,3), 0, 0);
	cvtColor(tmp, gray, CV_BGR2GRAY);
	Sobel(gray, gx, CV_16S, 1, 0);
	Sobel(gray, gy, CV_16S, 0, 1);

	convertScaleAbs(gx, gx);
	convertScaleAbs(gy, gy);//若不用绝对值，那么产出的图像就会缺失很多细节
	//addWeighted(gx, 0.5, gy, 0.5, 0, dst);

	dst = Mat(gx.size(), gx.type());
	//printf("type : %d\n", gx.type()); //这里能看到gx的type是0，即CV_8U，所以下面指针类型都是uchar
	int width = dst.cols;
	int height = dst.rows;
	for (int row = 0; row < height; row++)
	{
     
		for (int col = 0; col < width; col++)
		{
     	//每个取号绝对值的像素值都相加
			int xg = gx.at<uchar>(row, col);
			int yg = gy.at<uchar>(row, col);
			int xy = xg + yg;
			dst.at<uchar>(row, col) = saturate_cast<uchar>(xy);//指定像素值在0~255，防止被截断
		}
	}
	imshow("【输出图像】", dst);

	waitKey(0);
	return 0;
}

结果

可以看到，细节比上面加权相加多了很多

加权相加的结果如下

如果我们直接使用加权相加，丢失了一些细节，那么我们后续的处理可能会差的更远。所谓差之毫厘，谬以千里。
所以我们需要了解图像处理的本质。

Scharr算子

我们之前聊到梯度，即周围像素差值的变化率，要了解这个概念，我们就需要求导。

导数是对于连续函数来说的，图像差值不是连续的函数，所以这种方式，其实只是一个近似解。

这种近似解，对于上面的来说又不是特别的精确，所以，在opencv中，采用更加精确的Scharr算子：

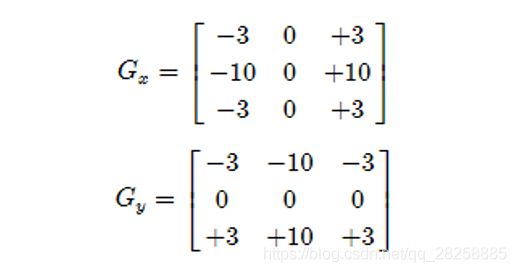
代码

#include
#include

using namespace std;
using namespace cv;

int main()
{
     
	Mat src, gx, gy, dst;

	src = imread("C:/Users/86176/Pictures/pics/lena(1).tiff");
	if (!src.data)
	{
     
		cout << "could not load image !";
		return -1;
	}
	imshow("【输入图像】", src);

	Mat tmp,gray;
	GaussianBlur(src, tmp, Size(3,3), 0, 0);
	cvtColor(tmp, gray, CV_BGR2GRAY);

	Scharr(gray, gx, CV_16S, 1, 0);
	Scharr(gray, gy, CV_16S, 0, 1);

	//Sobel(gray, gx, CV_16S, 1, 0);
	//Sobel(gray, gy, CV_16S, 0, 1);

	convertScaleAbs(gx, gx);
	convertScaleAbs(gy, gy);//若不用绝对值，那么产出的图像就会缺失很多细节
	//addWeighted(gx, 0.5, gy, 0.5, 0, dst);

	dst = Mat(gx.size(), gx.type());
	//printf("type : %d\n", gx.type()); //这里能看到gx的type是0，即CV_8U，所以下面指针类型都是uchar
	int width = dst.cols;
	int height = dst.rows;
	for (int row = 0; row < height; row++)
	{
     
		for (int col = 0; col < width; col++)
		{
     	//每个取号绝对值的像素值都相加
			int xg = gx.at<uchar>(row, col);
			int yg = gy.at<uchar>(row, col);
			int xy = xg + yg;
			dst.at<uchar>(row, col) = saturate_cast<uchar>(xy);//指定像素值在0~255，防止被截断
		}
	}
	imshow("【输出图像】", dst);

	waitKey(0);
	return 0;
}

结果

相较于Sobel，Scharr对图像的边缘有了更大的加强
即，Scharr对抗噪声的干扰强于Sobel