python数据结构与算法1

python数据结构与算法笔记

说明：本笔记参考B站学习视频自己总结而来

B站python数据结构与算法学习视频

day01背景介绍

算法重要性：

· 算法工程师
· 程序更高效–不一定去开发网站，去开发更高性能的算法，如人工智能（手动狗头）
· 算法题是公司入门的门槛

算法基础：

• 算法概念：algorithm（一个计算过程，结算问题的方法）数据结构–变量、列表、字典及其存储方式（静态的），算法–修改静态变量的过程即称为算法。算法经常封装为一个函数

• 时间复杂度：体现程序运行快慢的速度,用来评估算法运行效率的一个式子–O(1)中O为数学中上界的表示，1类似一个基本单位（对应于基本操作)，主要O()中需要标识的为1,n,n^2,logn

  • 当出现折半操作时一定会有logn出现
  • 常见的时间复杂度按效率排序1
  • 1层for循环定义为O(n),N层循环O(n^N)。
  • [机器设备]
  • [问题规模]

• 空间复杂度：用来评估算法内存占用大小的式子，表示方式与时间复杂度完全一样

  • 算法使用了几个变量O(1)
  • 算法使用了长度为n的一位列表：O(n)
  • 算法使用了m行n列的二维列表O(mn)
  • 空间换时间（内存发展至今，真不错）

• 递归：调用自身、结束条件

day02 递归解决实际问题

汉诺塔问题

（1）问题背景

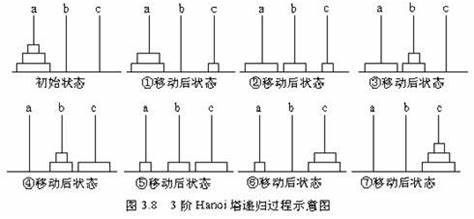
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

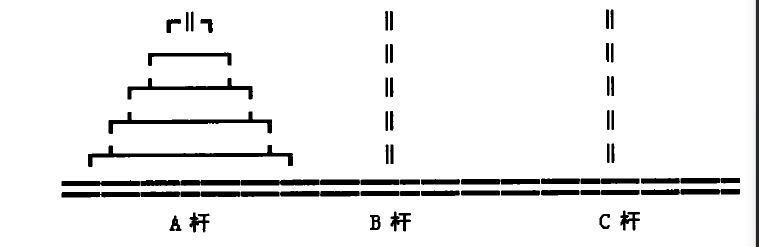
（2）问题简化–3个圆盘

（3）问题引申–n个圆盘

step1. 首先将最下面的1个盘子看为一个整体（即直接无视掉最下面的1个盘子），将上面的n-1个盘子看为一个整体
step2. 把n-1个盘子从A经过C移动到B（移动n-1个盘子）
step3. 把第n个盘子从A移动到C（移动1个盘子）
step4. 把n-1个盘子从B经过A移动到C（移动n-1个盘子）

· 从上面的步骤可以看出step2、step4可以看作是原问题的简化版，移动了n-1个盘子

（4）代码

def hanoi(n,a,b,c):#n个盘子从a移动到c
    if n>0:
        hanoi(n-1,a,c,b) #step1 （n-1个盘子从a经过c移动到b）
        print("moving the top one from %s to %s" % (a,c)) #step2（最下面的1个盘子）
        hanoi(n-1,b,a,c) #step3 （n-1个盘子从b经过a移动到c）

（5）一点小思考

• 汉诺塔移动次数的递归表达式h(x)=2h(x-1)+1
• h(2)=3 移动两个盘子需要三次
• maybe移动64个盘子完成后世界真的毁灭了
  

day03 查找问题

1.基本概念

1.（1）查找：在一些数据元素中，通过一定方法找出与给定关键字相同的数据元素的过程

1.（2）列表查找：从列表中查找指定元素

• 输入：列表、待查找元素
• 输出：元素下标（没有找到元素返回None或-1）
• 内置列表查找元素index()(源码对应顺序查找)

1.（3）查找算法分类1–静态or动态：静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。

1.（3）查找算法分类2–无序or有序：无序查找：被查找数列有序无序均可；有序查找：被查找数列必须为有序数列。

1.（4）平均查找长度（Average Search Length，ASL）：需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。

对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。
Pi：查找表中第i个数据元素的概率。
Ci：找到第i个数据元素时已经比较过的次数。

2.常用查找算法

2.1 顺序查找linear search

2.1（1）概念：顺序查找是按照序列原有顺序对数组进行遍历比较查询的基本查找算法。 对于任意一个序列以及一个给定的元素，将给定元素与序列中元素依次比较，直到找出与给定关键字相同的元素，或者将序列中的元素与其都比较完为止。

2.1（2）代码

def linear_search(Li,Val):
    for ind,v in enumerate(Li):
        if Val == v:
            return ind
    return None

时间复杂度：O(n)
时间复杂度分析：查找成功时的平均查找长度为(假设每个数据元素的概率相等)，ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;当查找不成功时，需要n+1次比较，时间复杂度为O(n)；所以，顺序查找的时间复杂度为O(n)。

2.1（3）说明：顺序查找适合于存储结构为顺序存储或链接存储的线性表。

2.2 二分查找linear search

2.2（1）概念：二分查找的实现原理非常简单，首先要有一个有序的列表。但是如果没有，则该怎么办？可以使用排序算法（详见后面的笔记）进行排序。以升序数列为例，比较一个元素与数列中的中间位置的元素的大小，如果比中间位置的元素大，则继续在后半部分的数列中进行二分查找；如果比中间位置的元素小，则在数列的前半部分进行比较；如果相等，则找到了元素的位置。每次比较的数列长度都会是之前数列的一半，直到找到相等元素的位置或者最终没有找到要找的元素。

2.2（2）优点：将原本线性查找时间提升到了对数查找时间范围（折半！！！折半！！！），大大缩短了搜索时间

2.2（3）代码

由于候选区缩小，因此需要维护一下候选区（最简单的方法是用两个变量维护left、right）

def binary_seearch(Li,Val):
    left = 0
    right = len(Li)-1
    while left <= right:  #保证候选去有值
        mid = (left+right) // 2  #整除2,非整除用/
        if Li[mid] == Val:
            return mid  #注意列表数组以0开始
        elif Li[mid] > Val: #待查找的值在mid左侧
            right = mid - 1
        else:
            left = mid + 1
    return None

复杂度分析：O(logn)
最坏情况下，关键词比较次数为log(n+1)，且期望时间复杂度为O(logn)；

2.2（4）说明：折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。

2.2（5）计算代码运行时间

###cal_time.py
import time

def cal_time(func):
    def wrapper(*args,**kwargs):
        t1 = time.time()
        result = func(*args,**kwargs)
        t2 = time.time()
        print("running time is %s" %(t2-t1))
        return result
    return wrapper

###search.py
from cal_time import *
@cal_time
def linear_search(Li,Val):
    for ind,v in enumerate(Li):
        if Val == v:
            return ind
    return None
@cal_time
def binary_seearch(Li,Val):
    left = 0
    right = len(Li)-1
    while left <= right:  #保证候选去有值
        mid = (left+right) // 2  #整除2,非整除用/
        if Li[mid] == Val:
            return mid  #注意列表数组以0开始
        elif Li[mid] > Val: #待查找的值在mid左侧
            right = mid - 1
        else:
            left = mid + 1
    return None
Li = list(range(10000000))
print(linear_search(Li,399999))
print(binary_seearch(Li,399999))

说明：上面的代码中使用了python里面的装饰器。下面引入博客python装饰器的知识

• python的装饰器本质上是一个Python函数，它可以让其他函数在不需要做任何代码变动的前提下增加额外功能，装饰器的返回值也是一个函数对象。
• 简单的说装饰器就是一个用来返回函数的函数。它经常用于有切面需求的场景，比如：插入日志、性能测试、事务处理、缓存、权限校验等场景。装饰器是解决这类问题的绝佳设计，有了装饰器，我们就可以抽离出大量与函数功能本身无关的雷同代码并继续重用。
• 概括的讲，装饰器的作用就是为已经存在的对象添加额外的功能。

补充1：装饰器语法糖

python提供了@符号作为装饰器的语法糖，使我们更方便的应用装饰函数。但使用语法糖要求装饰函数必须return一个函数对象。因此我们将上面的func函数使用内嵌函数包裹并return。
装饰器相当于执行了装饰函数use_loggin后又返回被装饰函数bar,因此bar()被调用的时候相当于执行了两个函数。等价于use_logging(bar)()

def use_logging(func):
  def _deco():
    print("%s is running" % func.__name__)
    func()
  return _deco
@use_logging
def bar():
  print('i am bar')
bar()

补充2：对带参数的函数进行装饰

现在我们的参数需要传入两个参数并计算值，因此我们需要对内层函数进行改动传入我们的两个参数a和b，等价于use_logging(bar)(1,2)

def use_logging(func):
  def _deco(a,b):
    print("%s is running" % func.__name__)
    func(a,b)
  return _deco
@use_logging
def bar(a,b):
  print('i am bar:%s'%(a+b))
bar(1,2)

我们装饰的函数可能参数的个数和类型都不一样，每一次我们都需要对装饰器做修改吗？这样做当然是不科学的，因此我们使用python的变长参数*args和**kwargs来解决我们的参数问题。

补充3：函数参数数量不确定

不带参数装饰器版本，这个格式适用于不带参数的装饰器。

经过以下修改我们已经适应了各种长度和类型的参数。这个版本的装饰器已经可以任意类型的无参数函数。

def use_logging(func):
  def _deco(*args,**kwargs):
    print("%s is running" % func.__name__)
    func(*args,**kwargs)
  return _deco
@use_logging
def bar(a,b):
  print('i am bar:%s'%(a+b))
@use_logging
def foo(a,b,c):
  print('i am bar:%s'%(a+b+c))
bar(1,2)
foo(1,2,3)

补充4：装饰器带参数

带参数的装饰器，这个格式适用于带参数的装饰器。
某些情况我们需要让装饰器带上参数，那就需要编写一个返回一个装饰器的高阶函数，写出来会更复杂。比如：

#! /usr/bin/env python
# -*- coding:utf-8 -*-
# __author__ = "TKQ"
def use_logging(level):
  def _deco(func):
    def __deco(*args, **kwargs):
      if level == "warn":
        print ("%s is running" % func.__name__)
      return func(*args, **kwargs)
    return __deco
  return _deco
@use_logging(level="warn")
def bar(a,b):
  print('i am bar:%s'%(a+b))
bar(1,3)
# 等价于use_logging(level="warn")(bar)(1,3)

补充5：functools.wraps

使用装饰器极大地复用了代码，但是他有一个缺点就是原函数的元信息不见了，比如函数的docstring、_name_、参数列表，例子：

def use_logging(func):
  def _deco(*args,**kwargs):
    print("%s is running" % func.__name__)
    func(*args,**kwargs)
  return _deco
@use_logging
def bar():
  print('i am bar')
  print(bar.__name__)
bar()
#bar is running
#i am bar
#_deco
#函数名变为_deco而不是bar，这个情况在使用反射的特性的时候就会造成问题。因此引入了functools.wraps解决这个问题。

使用functools.wraps:

import functools
def use_logging(func):
  @functools.wraps(func)
  def _deco(*args,**kwargs):
    print("%s is running" % func.__name__)
    func(*args,**kwargs)
  return _deco
@use_logging
def bar():
  print('i am bar')
  print(bar.__name__)
bar()
#result:
#bar is running
#i am bar
#bar ,这个结果是我们想要的。OK啦！

补充6：实现带参数和不带参数的装饰器自适应

import functools
def use_logging(arg):
  if callable(arg):#判断参入的参数是否是函数，不带参数的装饰器调用这个分支
    @functools.wraps(arg)
    def _deco(*args,**kwargs):
      print("%s is running" % arg.__name__)
      arg(*args,**kwargs)
    return _deco
  else:#带参数的装饰器调用这个分支
    def _deco(func):
      @functools.wraps(func)
      def __deco(*args, **kwargs):
        if arg == "warn":
          print "warn%s is running" % func.__name__
        return func(*args, **kwargs)
      return __deco
    return _deco
@use_logging("warn")
# @use_logging
def bar():
  print('i am bar')
  print(bar.__name__)
bar()

补充7：类装饰器

使用类装饰器可以实现带参数装饰器的效果，但实现的更加优雅简洁,而且可以通过继承来灵活的扩展.

class loging(object):
  def __init__(self,level="warn"):
    self.level = level
  def __call__(self,func):
    @functools.wraps(func)
    def _deco(*args, **kwargs):
      if self.level == "warn":
        self.notify(func)
      return func(*args, **kwargs)
    return _deco
  def notify(self,func):
    # logit只打日志，不做别的
    print ("%s is running" % func.__name__)
@loging(level="warn")#执行__call__方法
def bar(a,b):
  print('i am bar:%s'%(a+b))
bar(1,3)

继承扩展类装饰器

class email_loging(Loging):
  '''
  一个loging的实现版本，可以在函数调用时发送email给管理员
  '''
  def __init__(self, email='[email protected]', *args, **kwargs):
    self.email = email
    super(email_loging, self).__init__(*args, **kwargs)
  def notify(self,func):
    # 发送一封email到self.email
    print "%s is running" % func.__name__
    print "sending email to %s" %self.email
@email_loging(level="warn")
def bar(a,b):
  print('i am bar:%s'%(a+b))
bar(1,3)

喝杯咖啡缓缓神…lay了lay了

2.3 插值查找

2.3（1）概念：插值查找算法又称插值搜索算法，是二分查找算法的改进版，它将查找点的选择改进为自适应选择，从而间接减少了查找次数。和二分查找算法相同，插值查找算法也仅适用于有序序列。 此外，当有序序列中的元素呈现均匀分布时，插值查找算法的执行效率比二分查找算法更高。 也就是说，插值查找算法适用于均匀分布的有序序列。

插值查找：mid=low+(key-li[low])/(li[high]-li[low])*(high-low)    
二分查找：mid=low+1/2*(high-low)

2.3（2）代码

def interpolation_seearch(Li,Val):
    left = 0
    right = len(Li)-1
    while left <= right:
        mid = left + int((right - left) * (Val - Li[left])/(Li[right] - Li[left]))
        if Li[mid] == Val:
            return mid
        elif Li[mid] > Val:
            right = mid - 1
        else:
            left = mid + 1
    return None

查找成功或者失败的时间复杂度均为O(log(logn))。

2.3（3）注意：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

2.4 斐波那契查找

2.4（1）背景–黄金分割

• 在介绍斐波那契查找算法之前，我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。
• 黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。
• 0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。
• 大家记不记得斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性（F(n)=F(n-1)+F(n-2)），我们就可以将黄金比例运用到查找技术中。

2.4（2）算法思想

• 斐波那契查找通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。他是根据斐波那契序列的特点对有序表进行分割的（二分查找的改进）。
  
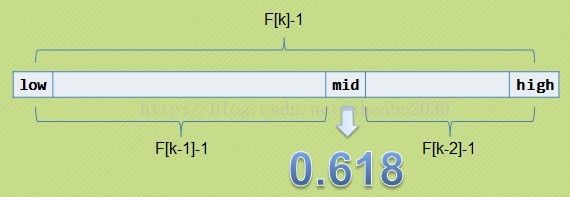
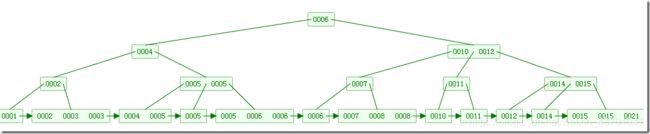
• 特点：要求开始表中数据的个数len为某个斐波那契数减1，即len=F(n)-1（该长度可以循环切割，见上图，中间的一个值即为要设定的mid值）
  mid= low +F[n-1] - 1
• 算法步骤：
  • step1.构建斐波那契数列（[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377]）
  • step2.将数据列表的长度len扩充为某个斐波那契数减1，即len=F(n)-1。如原来的数组长度为25，比25大的最近的的斐波那契数值为34，由此将数字从25个元素填充到33个，填充时，将第26到33个元素均采用第25个元素值进行填充，即最大值填充。
  • step3. 循环进行区间分割，查找中间值Li(mid)，其中mid=low+F(n-1)-1，比较结果也分为三种
    • 相等，则查找成功，返回中间位置即可；
    • 中间值小于目标值，则说明目标值位于中间值到右边界之间（即右区间），右区间含有F(n-2)个元素，所以n应该更新为n=n-2；
      说明：更新low=mid+1，n=n-2，说明待查找的元素在[mid+1,high]范围内，n=n-2 说明范围[mid+1,high]内的元素个数为len-(F(n-1))= F(n)-1-F(n-1)=F(n-2)-1个，所以可以递归的应用斐波那契查找。
    • 中间值大于目标值，这说明目标值位于左边界和中间值之间（即左区间），左区间含有F(n-1)个元素，所以n应更新为n=n-1；
      更新high=mid-1,n=n-1。

2.4（3）代码

fib = lambda n: n if n < 2 else fib(n - 1) + fib(n - 2)
def fib_search(arr, val):
    if len(arr) == 0:
        return 'arr is None'

    left = 0
    right = len(arr) - 1

    # 计算fib的值，这个值是大于等于arr的长度的，所以使用时要对key-1
    key = 0
    while fib(key) < len(arr):
        key += 1

    while left <= right:
        # 当x在分隔的后半部分时，fib计算的mid值可能大于arr长度
        # 因为mid是索引位置，这里要取arr长度-1
        mid = min(left + fib(key - 1) - 1, len(arr) - 1)
        if val < arr[mid]:
            right = mid - 1
            key -= 1
        elif val > arr[mid]:
            left = mid + 1
            key -= 2
        else:
            return mid
    return -1


def test_fib_search():
    arr = [1, 8, 10, 89, 1000, 1234]
    print(fib_search(arr, 1000)) # 4


if __name__ == '__main__':
    test_fib_search()

复杂度分析：最坏情况下，时间复杂度为O(logn)，且其期望复杂度也为O(logn)。

2.5 树表查找

2.5.1最简单的树表查找算法——二叉树查找算法

2.5.1（1）基本思想：二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。

2.5.1（2）二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree）或者是一棵空树，或者是具有下列性质的二叉树：

1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3）任意节点的左、右子树也分别为二叉查找树。

二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列。

2.5.1（3）不同形态的二叉查找树如下图所示：

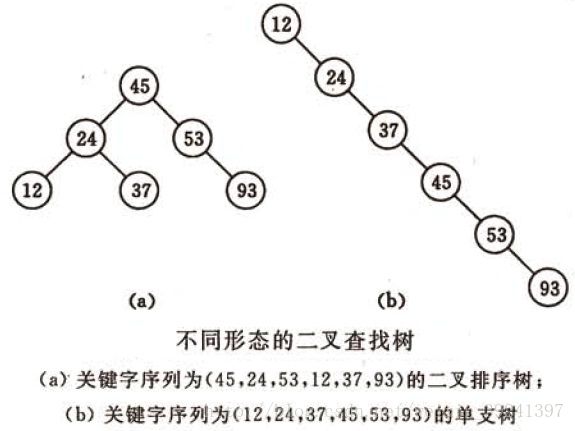
复杂度分析：它和二分查找一样，插入和查找的时间复杂度均为O(logn)，但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡（比如，我们查找上图（b）中的“93”，我们需要进行n次查找操作）。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是平衡查找树设计的初衷。

2.5.1（4）二叉树查找和顺序查找以及二分查找性能的对比图：

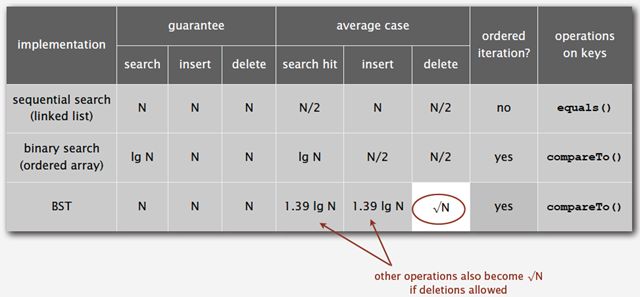
基于二叉查找树进行优化，进而可以得到其他的树表查找算法，如平衡树、红黑树等高效算法

2.5.1（5）二叉查找树完整代码

学习链接：
https://blog.csdn.net/u010089444/article/details/70854510

# encoding: utf-8
class Node:
    def __init__(self, data):
        self.data = data
        self.lchild = None
        self.rchild = None

class BST:
    def __init__(self, node_list):
        self.root = Node(node_list[0])
        for data in node_list[1:]:
            self.insert(data)

    # 搜索
    def search(self, node, parent, data):
        if node is None:
            return False, node, parent
        if node.data == data:
            return True, node, parent
        if node.data > data:
            return self.search(node.lchild, node, data)
        else:
            return self.search(node.rchild, node, data)

    # 插入
    def insert(self, data):
        flag, n, p = self.search(self.root, self.root, data)
        if not flag:
            new_node = Node(data)
            if data > p.data:
                p.rchild = new_node
            else:
                p.lchild = new_node

    # 删除
    def delete(self, root, data):
        flag, n, p = self.search(root, root, data)
        if flag is False:
            print "无该关键字，删除失败"
        else:
            if n.lchild is None:
                if n == p.lchild:
                    p.lchild = n.rchild
                else:
                    p.rchild = n.rchild
                del p
            elif n.rchild is None:
                if n == p.lchild:
                    p.lchild = n.lchild
                else:
                    p.rchild = n.lchild
                del p
            else:  # 左右子树均不为空
                pre = n.rchild
                if pre.lchild is None:
                    n.data = pre.data
                    n.rchild = pre.rchild
                    del pre
                else:
                    next = pre.lchild
                    while next.lchild is not None:
                        pre = next
                        next = next.lchild
                    n.data = next.data
                    pre.lchild = next.rchild
                    del p


    # 先序遍历
    def preOrderTraverse(self, node):
        if node is not None:
            print node.data,
            self.preOrderTraverse(node.lchild)
            self.preOrderTraverse(node.rchild)

    # 中序遍历
    def inOrderTraverse(self, node):
        if node is not None:
            self.inOrderTraverse(node.lchild)
            print node.data,
            self.inOrderTraverse(node.rchild)

    # 后序遍历
    def postOrderTraverse(self, node):
        if node is not None:
            self.postOrderTraverse(node.lchild)
            self.postOrderTraverse(node.rchild)
            print node.data,

a = [49, 38, 65, 97, 60, 76, 13, 27, 5, 1]
bst = BST(a)  # 创建二叉查找树
bst.inOrderTraverse(bst.root)  # 中序遍历

bst.delete(bst.root, 49)
print
bst.inOrderTraverse(bst.root)

2.5.2平衡查找树之2-3查找树（2-3 Tree）

2.5.2（1）定义：

2-3 Tree和二叉树不一样，2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node)，他保存1个key和左右两个自己点。对应3节点(3-node)，保存两个Key，2-3查找树的定义如下：
1）要么为空，要么：
2）对于2节点，2节点包含一个元素和两个孩子（或者没有孩子），两个孩子指针指向了左右子树指针，如果存在的话，左子树包含节点的元素的值小于该节点的元素值，右子树包含的节点的元素值大于该节点的元素值
3）对于3节点，3节点包含一大一小两个元素（两个元素按大小顺序排列好）和三个孩子（或者没有孩子）。左子树包含的节点的元素值小于该节点较小的元素值，右子树包含的节点的元素值大于该节点较大的元素值，中间子树包含的节点的元素值介于这两个元素之间
示例图(这里以字母的顺序为大小进行比较)

• 总结可以得出23tree中所有节点的分支树比值的个数多1，最后一行分支的指针值都是null

2.5.2（2）性质：

1）如果中序遍历2-3查找树，就可以得到排好序的序列；
2）在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。（这也是平衡树中“平衡”一词的概念，根节点到叶节点的最长距离对应于查找算法的最坏情况，而平衡树中根节点到叶节点的距离都一样，最坏情况也具有对数复杂度。）
性质2）如下图所示：

2.5.2（3）复杂度分析：

1）2-3树的查找效率与树的高度是息息相关的。

• 在最坏的情况下，也就是所有的节点都是2-node节点，查找效率为lgN
• 在最好的情况下，所有的节点都是3-node节点，查找效率为log3N约等于0.631lgN

2）从距离的角度分析，对于1百万个节点的2-3树，树的高度为12-20之间，对于10亿个节点的2-3树，树的高度为18-30之间。

3）对于插入来说，只需要常数次操作即可完成，因为他只需要修改与该节点关联的节点即可，不需要检查其他节点，所以效率和查找类似。下面是2-3查找树的效率：

2.5.2（4）2-3树代码实现

class Node(object):
    def __init__(self,key):
        self.key1=key
        self.key2=None
        self.left=None
        self.middle=None
        self.right=None
    def isLeaf(self):
        return self.left is None and self.middle is None and self.right is None
    def isFull(self):
        return self.key2 is not None
    def hasKey(self,key):
        if (self.key1==key) or (self.key2 is not None and self.key2==key):
            return True
        else:
            return False
    def getChild(self,key):
        if key<self.key1:
            return self.left
        elif self.key2 is None:
            return self.middle
        elif key<self.key2:
            return self.middle
        else:
            return self.right
class 2_3_Tree(object):
    def __init__(self):
        self.root=None
    def get(self,key):
        if self.root is None:
            return None
        else:
            return self._get(self.root,key)
    def _get(self,node,key):
        if node is None:
            return None
        elif node.hasKey(key):
            return node
        else:
            child=node.getChild(key)
            return self._get(child,key)
    def put(self,key):
        if self.root is None:
            self.root=Node(key)
        else:
            pKey,pRef=self._put(self.root,key)
            if pKey is not None:
                newnode=Node(pKey)
                newnode.left=self.root
                newnode.middle=pRef
                self.root=newnode
    def _put(self,node,key):
        if node.hasKey(key):
            return None,None
        elif node.isLeaf():
            return self._addtoNode(node,key,None)
        else:
            child=node.getChild(key)
            pKey,pRef=self._put(child,key)
            if pKey is None:
                return None,None
            else:
                return self._addtoNode(node,pKey,pRef)
             
         
    def _addtoNode(self,node,key,pRef):
        if node.isFull():
            return self._splitNode(node,key,pRef)
        else:
            if key<node.key1:
                node.key2=node.key1
                node.key1=key
                if pRef is not None:
                    node.right=node.middle
                    node.middle=pRef
            else:
                node.key2=key
                if pRef is not None:
                    node.right=Pref
            return None,None
    def _splitNode(self,node,key,pRef):
        newnode=Node(None)
        if key<node.key1:
            pKey=node.key1
            node.key1=key
            newnode.key1=node.key2
            if pRef is not None:
                newnode.left=node.middle
                newnode.middle=node.right
                node.middle=pRef
        elif key<node.key2:
            pKey=key
            newnode.key1=node.key2
            if pRef is not None:
                newnode.left=Pref
                newnode.middle=node.right
        else:
            pKey=node.key2
            newnode.key1=key
            if pRef is not None:
                newnode.left=node.right
                newnode.middle=pRef
        node.key2=None
        return pKey,newnode

2.5.3平衡查找树值红黑树（Red-Black Tree）

2.5.3（1）背景介绍

2-3查找树能保证在插入元素之后能保持树的平衡状态，最坏情况下即所有的子节点都是2-node，树的高度为logn，从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂，于是就有了一种简单实现2-3树的数据结构，即红黑树（Red-Black Tree）。

2.5.3（2）基本思想

红黑树的思想就是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

2.5.3（3）红黑树的定义

红黑树是一种具有红色和黑色链接的平衡查找树，同时满足：

• 红色节点向左倾斜
• 一个节点不可能有两个红色链接
• 整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

下图可以看到红黑树其实是2-3树的另外一种表现形式：如果我们将红色的连线水平绘制，那么他链接的两个2-node节点就是2-3树中的一个3-node节点了。

2.5.3（4）红黑树的性质及分析

• 红黑树的性质：整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同（2-3树的第2）性质，从根节点到叶子节点的距离都相等）。
• 复杂度分析：最坏的情况就是，红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。

下图是一个典型的红黑树，从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍：

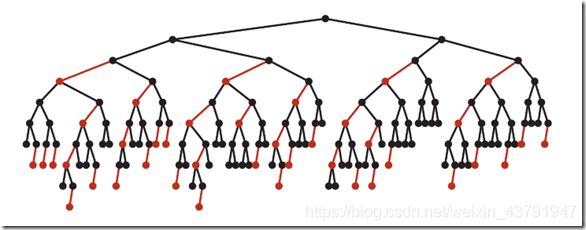
• 红黑树的平均高度大约为logn。

下图是红黑树在各种情况下的时间复杂度，可以看出红黑树是2-3查找树的一种实现，它能保证最坏情况下仍然具有对数的时间复杂度。

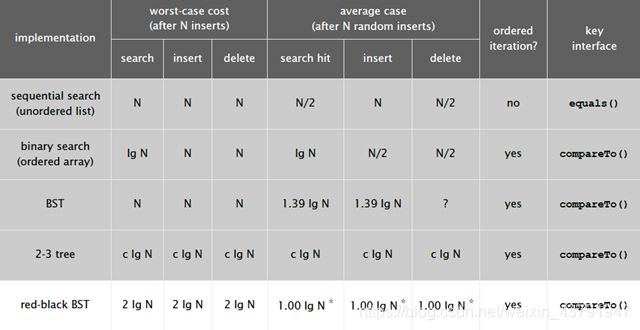
2.5.3（5）代码及深入学习

红黑树深入学习

#红黑树
from random import randint

RED = 'red'
BLACK = 'black'

class RBT:
    def __init__(self):
       # self.items = []
        self.root = None
        self.zlist = []

    def LEFT_ROTATE(self, x):
        # x是一个RBTnode
        y = x.right
        if y is None:
            # 右节点为空，不旋转
            return
        else:
            beta = y.left
            x.right = beta
            if beta is not None:
                beta.parent = x

            p = x.parent
            y.parent = p
            if p is None:
                # x原来是root
                self.root = y
            elif x == p.left:
                p.left = y
            else:
                p.right = y
            y.left = x
            x.parent = y

    def RIGHT_ROTATE(self, y):
        # y是一个节点
        x = y.left
        if x is None:
            # 右节点为空，不旋转
            return
        else:
            beta = x.right
            y.left = beta
            if beta is not None:
                beta.parent = y

            p = y.parent
            x.parent = p
            if p is None:
                # y原来是root
                self.root = x
            elif y == p.left:
                p.left = x
            else:
                p.right = x
            x.right = y
            y.parent = x

    def INSERT(self, val):

        z = RBTnode(val)
        y = None
        x = self.root
        while x is not None:
            y = x
            if z.val < x.val:
                x = x.left
            else:
                x = x.right

        z.PAINT(RED)
        z.parent = y

        if y is None:
            # 插入z之前为空的RBT
            self.root = z
            self.INSERT_FIXUP(z)
            return

        if z.val < y.val:
            y.left = z
        else:
            y.right = z

        if y.color == RED:
            # z的父节点y为红色，需要fixup。
            # 如果z的父节点y为黑色，则不用调整
            self.INSERT_FIXUP(z)

        else:
            return

    def INSERT_FIXUP(self, z):
        # case 1:z为root节点
        if z.parent is None:
            z.PAINT(BLACK)
            self.root = z
            return

        # case 2:z的父节点为黑色
        if z.parent.color == BLACK:
            # 包括了z处于第二层的情况
            # 这里感觉不必要啊。。似乎z.parent为黑色则不会进入fixup阶段
            return

        # 下面的几种情况，都是z.parent.color == RED:
        # 节点y为z的uncle
        p = z.parent
        g = p.parent  # g为x的grandpa
        if g is None:
            return
            #   return 这里不能return的。。。
        if g.right == p:
            y = g.left
        else:
            y = g.right

        # case 3-0:z没有叔叔。即：y为NIL节点
        # 注意，此时z的父节点一定是RED
        if y == None:
            if z == p.right and p == p.parent.left:
                # 3-0-0:z为右儿子,且p为左儿子，则把p左旋
                # 转化为3-0-1或3-0-2的情况
                self.LEFT_ROTATE(p)
                p, z = z, p
                g = p.parent
            elif z == p.left and p == p.parent.right:
                self.RIGHT_ROTATE(p)
                p, z = z, p

            g.PAINT(RED)
            p.PAINT(BLACK)
            if p == g.left:
                # 3-0-1:p为g的左儿子
                self.RIGHT_ROTATE(g)
            else:
                # 3-0-2:p为g的右儿子
                self.LEFT_ROTATE(g)

            return

        # case 3-1:z有黑叔
        elif y.color == BLACK:
            if p.right == z and p.parent.left == p:
                # 3-1-0:z为右儿子,且p为左儿子,则左旋p
                # 转化为3-1-1或3-1-2
                self.LEFT_ROTATE(p)
                p, z = z, p
            elif p.left == z and p.parent.right == p:
                self.RIGHT_ROTATE(p)
                p, z = z, p

            p = z.parent
            g = p.parent

            p.PAINT(BLACK)
            g.PAINT(RED)
            if p == g.left:
                # 3-1-1:p为g的左儿子，则右旋g
                self.RIGHT_ROTATE(g)
            else:
                # 3-1-2:p为g的右儿子，则左旋g
                self.LEFT_ROTATE(g)

            return


        # case 3-2:z有红叔
        # 则涂黑父和叔，涂红爷，g作为新的z，递归调用
        else:
            y.PAINT(BLACK)
            p.PAINT(BLACK)
            g.PAINT(RED)
            new_z = g
            self.INSERT_FIXUP(new_z)

    def DELETE(self, val):
        curNode = self.root
        while curNode is not None:
            if val < curNode.val:
                curNode = curNode.left
            elif val > curNode.val:
                curNode = curNode.right
            else:
                # 找到了值为val的元素,正式开始删除

                if curNode.left is None and curNode.right is None:
                    # case1:curNode为叶子节点：直接删除即可
                    if curNode == self.root:
                        self.root = None
                    else:
                        p = curNode.parent
                        if curNode == p.left:
                            p.left = None
                        else:
                            p.right = None

                elif curNode.left is not None and curNode.right is not None:
                    sucNode = self.SUCCESOR(curNode)
                    curNode.val, sucNode.val  = sucNode.val, curNode.val
                    self.DELETE(sucNode.val)

                else:
                    p = curNode.parent
                    if curNode.left is None:
                        x = curNode.right
                    else:
                        x = curNode.left
                    if curNode == p.left:
                        p.left = x
                    else:
                        p.right = x
                    x.parent = p
                    if curNode.color == BLACK:
                        self.DELETE_FIXUP(x)

                curNode = None
        return False

    def DELETE_FIXUP(self, x):
        p = x.parent
        # w:x的兄弟结点
        if x == p.left:
            w = x.right
        else:
            w = x.left

        # case1:x的兄弟w是红色的
        if w.color == RED:
            p.PAINT(RED)
            w.PAINT(BLACK)
            if w == p.right:
                self.LEFT_ROTATE(p)
            else:
                self.RIGHT_ROTATE(p)

        if w.color == BLACK:
            # case2:x的兄弟w是黑色的，而且w的两个孩子都是黑色的
            if w.left.color == BLACK and w.right.color == BLACK:
                w.PAINT(RED)
                if p.color == BLACK:
                    return
                else:
                    p.color = BLACK
                    self.DELETE_FIXUP(p)

            # case3:x的兄弟w是黑色的，而且w的左儿子是红色的，右儿子是黑色的
            if w.left.color == RED and w.color == BLACK:
                w.left.PAINT(BLACK)
                w.PAINT(RED)
                self.RIGHT_ROTATE(w)

            # case4:x的兄弟w是黑色的，而且w的右儿子是红
            if w.right.color == RED:
                p.PAINT(BLACK)
                w.PAINT(RED)
                if w == p.right:
                    self.LEFT_ROTATE(p)
                else:
                    self.RIGHT_ROTATE(p)

    def SHOW(self):
        self.DISPLAY1(self.root)
        return self.zlist

    def DISPLAY1(self, node):
        if node is None:
            return
        self.DISPLAY1(node.left)
        self.zlist.append(node.val)
        self.DISPLAY1(node.right)

    def DISPLAY2(self, node):
        if node is None:
            return
        self.DISPLAY2(node.left)
        print(node.val)
        self.DISPLAY2(node.right)

    def DISPLAY3(self, node):
        if node is None:
            return
        self.DISPLAY3(node.left)
        self.DISPLAY3(node.right)
        print(node.val)

class RBTnode:
    '''红黑树的节点类型'''
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.parent = None

    def PAINT(self, color):
        self.color = color

def zuoxuan(b, c):
    a = b.parent
    a.left = c
    c.parent = a
    b.parent = c
    c.left = b

if __name__ == '__main__':
    rbt=RBT()
    b = []

    for i in range(100):
        m = randint(0, 500)
        rbt.INSERT(m)
        b.append(m)

    a = rbt.SHOW()
    b.sort()
    equal = True
    for i in range(100):
        if a[i] != b[i]:
            equal = False
            break

    if not equal:
        print('wrong')
    else:
        print('OK!')

2.5.4 B树和B+树（B Tree/B+ Tree）

2.5.4 （1）背景介绍

维基百科对B树的定义为“在计算机科学中，B树（B-tree）是一种树状数据结构，它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树，概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同，B树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程，从而加快存取速度。普遍运用在数据库和文件系统。

2.5.4 （2）B树定义

B树可以看作是对2-3查找树的一种扩展，我们把树中节点最大的孩子数目称为B树的阶，通常记为m，一棵m阶B树或为空树或为满足如下特征的m叉树：

• 根节点至少有两个子节点
• 每个节点有M-1个值，并且以升序排列。每个节点最多有M棵子树
• 除去根节点外其它节点至少有M/2个子节点
• 所有的叶子节点出现在同一层次上，不带信息
• example:2-3树的节点M=3

下图是一个M=4

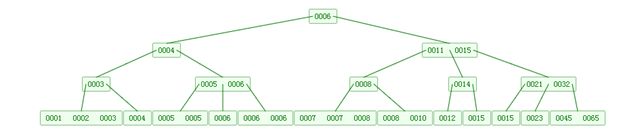
可以看到B树是2-3树的一种扩展，他允许一个节点有多于2个的元素。B树的插入及平衡化操作和2-3树很相似，这里就不介绍了。

--------------------------------------------------------------------------

下面是往B树中依次插入
6 10 4 14 5 11 15 3 2 12 1 7 8 8 6 3 6 21 5 15 15 6 32 23 45 65 7 8 6 5 4
的演示动画：

2.5.4 （3）B树常用的的操作

官方链接：https://pythonhosted.org/BTrees/

1. B树的查找操作
2. B树的建立：从空树中依次插入–>插入操作（注意节点的分裂和连续分裂）
3. B树的删除操作–终端节点、不在终端节点

2.5.4 （4）B+树定义

B+树是对B树的一种变形树，它与B树的差异在于：

• 有k个子结点的结点必然有k个关键码；
• 非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。
• 树的所有叶结点构成一个有序链表，可以按照关键码排序的次序遍历全部记录。

如下图，是一个B+树:

下图是B+树的插入动画

B+Tree相对于B-Tree有几点不同：

• 非叶子节点只存储键值信息。
• 所有叶子节点之间都有一个链指针。
• 数据记录都存放在叶子节点中。

2.5.4 （5）B+树特点

B+树算法思想

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+树的特性

  1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的；
  2.不可能在非叶子结点命中；
  3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层；
  4.更适合文件索引系统；

2.5.4 （6）B树算法实现

# -*- coding: UTF-8 -*-
# B树查找

class BTree:  #B树
    def __init__(self,value):
        self.left=None
        self.data=value
        self.right=None

    def insertLeft(self,value):
        self.left=BTree(value)
        return self.left

    def insertRight(self,value):
        self.right=BTree(value)
        return self.right

    def show(self):
        print(self.data)


def inorder(node):  #中序遍历：先左子树，再根节点，再右子树
    if node.data:
        if node.left:
            inorder(node.left)
        node.show()
        if node.right:
            inorder(node.right)


def rinorder(node):  #倒中序遍历
    if node.data:
        if node.right:
            rinorder(node.right)
        node.show()
        if node.left:
            rinorder(node.left)

def insert(node,value):
    if value > node.data:
        if node.right:
            insert(node.right,value)
        else:
            node.insertRight(value)
    else:
        if node.left:
            insert(node.left,value)
        else:
            node.insertLeft(value)


if __name__ == "__main__":

    l=[88,11,2,33,22,4,55,33,221,34]
    Root=BTree(l[0])
    node=Root
    for i in range(1,len(l)):
        insert(Root,l[i])

    print("中序遍历（从小到大排序 ）")
    inorder(Root)
    print("倒中序遍历（从大到小排序）")
    rinorder(Root)

2.5.4 （7）树表查找总结

• 二叉查找树平均查找性能不错，为O(logn)，但是最坏情况会退化为O(n)。在二叉查找树的基础上进行优化，我们可以使用平衡查找树。平衡查找树中的2-3查找树，这种数据结构在插入之后能够进行自平衡操作，从而保证了树的高度在一定的范围内进而能够保证最坏情况下的时间复杂度。但是2-3查找树实现起来比较困难，红黑树是2-3树的一种简单高效的实现，他巧妙地使用颜色标记来替代2-3树中比较难处理的3-node节点问题。红黑树是一种比较高效的平衡查找树，应用非常广泛，很多编程语言的内部实现都或多或少的采用了红黑树。
• 除此之外，2-3查找树的另一个扩展——B/B+平衡树，在文件系统和数据库系统中有着广泛的应用。

2.6 分块查找

2.6（1） 算法简介

要求是顺序表，分块查找又称索引顺序查找，它是顺序查找的一种改进方法。 

2.6（2） 算法思想

• 将n个数据元素"按块有序"划分为m块（m ≤ n）。
• 每一块中的结点不必有序，但块与块之间必须"按块有序"；
• 即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字；而第2块中任一元素又都必须小于第3块中的任一元素，……

2.6（3） 算法流程

1、先选取各块中的最大关键字构成一个索引表；
2、查找分两个部分：先对索引表进行二分查找或顺序查找，以确定待查记录在哪一块中；
3、在已确定的块中用顺序法进行查找。

2.6（4）复杂度分析

时间复杂度：O(log(m)+N/m)

2.7 哈希查找

2.7（1） 算法简介

哈希表就是一种以键-值(key-indexed) 存储数据的结构，只要输入待查找的值即key，即可查找到其对应的值。

2.7（2） 算法思想

哈希的思路很简单，如果所有的键都是整数，那么就可以使用一个简单的无序数组来实现：将键作为索引，值即为其对应的值，这样就可以快速访问任意键的值。这是对于简单的键的情况，我们将其扩展到可以处理更加复杂的类型的键。

2.7（3） 算法流程

1）用给定的哈希函数构造哈希表；
2）根据选择的冲突处理方法解决地址冲突；常见的解决冲突的方法：拉链法和线性探测法。
3）在哈希表的基础上执行哈希查找。

2.7（4）复杂度分析

单纯论查找复杂度：对于无冲突的Hash表而言，查找复杂度为O(1)（注意，在查找之前我们需要构建相应的Hash表）。

2.7（5）算法实现

参考博客

# 忽略了对数据类型，元素溢出等问题的判断。
 
class HashTable:
  def __init__(self, size):
    self.elem = [None for i in range(size)] # 使用list数据结构作为哈希表元素保存方法
    self.count = size # 最大表长
 
  def hash(self, key):
    return key % self.count # 散列函数采用除留余数法
 
  def insert_hash(self, key):
    """插入关键字到哈希表内"""
    address = self.hash(key) # 求散列地址
    while self.elem[address]: # 当前位置已经有数据了，发生冲突。
      address = (address+1) % self.count # 线性探测下一地址是否可用
    self.elem[address] = key # 没有冲突则直接保存。
 
  def search_hash(self, key):
    """查找关键字，返回布尔值"""
    star = address = self.hash(key)
    while self.elem[address] != key:
      address = (address + 1) % self.count
      if not self.elem[address] or address == star: # 说明没找到或者循环到了开始的位置
        return False
    return True
 
 
if __name__ == '__main__':
  list_a = [12, 67, 56, 16, 25, 37, 22, 29, 15, 47, 48, 34]
  hash_table = HashTable(12)
  for i in list_a:
    hash_table.insert_hash(i)
 
  for i in hash_table.elem:
    if i:
      print((i, hash_table.elem.index(i)), end=" ")
  print("\n")
 
  print(hash_table.search_hash(15))
  print(hash_table.search_hash(33))

参考资料

1.https://www.cnblogs.com/lsqin/p/9342929.html
2.https://www.cnblogs.com/maybe2030/p/4715035.html#_labelTop
3.https://www.bilibili.com/video/BV1uA411N7c5?p=11&spm_id_from=pageDriver