一、神经网络的构造
- PyTorch中神经网络构造一般是基于
Module类的模型来完成的,它让模型构造更加灵活。Module类是nn模块里提供的一个模型构造类,是所有神经网络模块的基类,我们可以继承它来定义我们想要的模型。 - 下面继承
Module类构造多层感知机。这里定义的 MLP 类重载了Module类的init函数和forward函数。它们分别用于创建模型参数和定义前向计算。前向计算也即正向传播。
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 09:43:21 2021
@author: 86493
"""
import torch
from torch import nn
class MLP(nn.Module):
# 声明带有模型参数的层,此处声明了2个全连接层
def __init__(self, **kwargs):
# 调用MLP父类Block的构造函数来进行必要的初始化
# 这样在构造实例时还可以指定其他函数
super(MLP, self).__init__(**kwargs)
self.hidden = nn.Linear(784, 256)
self.act = nn.ReLU()
self.output = nn.Linear(256, 10)
# 定义模型的前向计算
# 即如何根据输入x计算返回所需要的模型输出
def forward(self, x):
o = self.act(self.hidden(x))
return self.output(o)
X = torch.rand(2, 784)
net = MLP()
print(net)
print('-' * 60)
print(net(X))
结果为:
MLP(
(hidden): Linear(in_features=784, out_features=256, bias=True)
(act): ReLU()
(output): Linear(in_features=256, out_features=10, bias=True)
)
------------------------------------------------------------
tensor([[ 0.1836, 0.1946, 0.0924, -0.1163, -0.2914, -0.1103, -0.0839, -0.1274,
0.1618, -0.0601],
[ 0.0738, 0.2369, 0.0225, -0.1514, -0.3787, -0.0551, -0.0836, -0.0496,
0.1481, 0.0139]], grad_fn=)
注意:
(1)上面的MLP类不需要定义反向传播函数,系统将通过自动求梯度而自动生成反向传播所需的backward函数。
(2)将数据X传入实例化MLP类后得到的net对象,会做一次前向计算,并且net(X)会调用MLP类继承自父类Module的call函数——该函数调用我们定义的子类MLP的forward函数完成前向传播计算。
(3)这里没将Module类命名为Layer(层)或者Model(模型)等,是因为该类是一个可供自由组建的部件, 它的子类既可以是一个层(如继承父类nn的子类线性层Linear),也可以是一个模型(如此处的子类MLP),也可以是模型的一部分。
二、神经网络中常见的层
有全连接层、卷积层、池化层与循环层等,下面学习使用Module定义层。
2.1 不含模型参数的层
下面构造的 MyLayer 类通过继承 Module 类自定义了一个将输入减掉均值后输出的层,并将层的计算定义在了 forward 函数里。这个层里不含模型参数。
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 10:19:59 2021
@author: 86493
"""
import torch
from torch import nn
class MyLayer(nn.Module):
def __init__(self, **kwargs):
# 调用父类的方法
super(MyLayer, self).__init__(**kwargs)
def forward(self, x):
return x - x.mean()
# 测试,实例化该层,做前向计算
layer = MyLayer()
layer1 = layer(torch.tensor([1, 2, 3, 4, 5],
dtype = torch.float))
print(layer1)
结果为:
tensor([-2., -1., 0., 1., 2.])
2.2 含模型参数的层
可以自定义含模型参数的自定义层。其中的模型参数可以通过训练学出。
Parameter 类其实是 Tensor 的子类,如果一个 Tensor 是 Parameter ,那么它会自动被添加到模型的参数列表里。所以在自定义含模型参数的层时,我们应该将参数定义成 Parameter ,除了直接定义成 Parameter 类外,还可以使用 ParameterList 和 ParameterDict 分别定义参数的列表和字典。
PS:下面出现torch.mm是将两个矩阵相乘,如
# -*- coding: utf-8 -*- """ Created on Sat Oct 16 10:56:03 2021 @author: 86493 """ import torch a = torch.randn(2, 3) b = torch.randn(3, 2) print(torch.mm(a, b)) # 效果相同 print(torch.matmul(a, b)) #tensor([[1.8368, 0.4065], # [2.7972, 2.3096]]) #tensor([[1.8368, 0.4065], # [2.7972, 2.3096]])
(1)代码栗子1
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 10:33:04 2021
@author: 86493
"""
import torch
from torch import nn
class MyListDense(nn.Module):
def __init__(self):
super(MyListDense, self).__init__()
# 3个randn的意思
self.params = nn.ParameterList([nn.Parameter(torch.randn(4, 4)) for i in range(3)])
self.params.append(nn.Parameter(torch.randn(4, 1)))
def forward(self, x):
for i in range(len(self.params)):
# mm是指矩阵相乘
x = torch.mm(x, self.params[i])
return x
net = MyListDense()
print(net)
打印得:
MyListDense(
(params): ParameterList(
(0): Parameter containing: [torch.FloatTensor of size 4x4]
(1): Parameter containing: [torch.FloatTensor of size 4x4]
(2): Parameter containing: [torch.FloatTensor of size 4x4]
(3): Parameter containing: [torch.FloatTensor of size 4x1]
)
)
(2)代码栗子2
这回用变量字典:
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 11:03:29 2021
@author: 86493
"""
import torch
from torch import nn
class MyDictDense(nn.Module):
def __init__(self):
super(MyDictDense, self).__init__()
self.params = nn.ParameterDict({
'linear1': nn.Parameter(torch.randn(4, 4)),
'linear2': nn.Parameter(torch.randn(4, 1))
})
# 新增
self.params.update({'linear3':
nn.Parameter(torch.randn(4, 2))})
def forward(self, x, choice = 'linear1'):
return torch.mm(x, self.params[choice])
net = MyDictDense()
print(net)
打印得:
MyDictDense(
(params): ParameterDict(
(linear1): Parameter containing: [torch.FloatTensor of size 4x4]
(linear2): Parameter containing: [torch.FloatTensor of size 4x1]
(linear3): Parameter containing: [torch.FloatTensor of size 4x2]
)
)
2.3 二维卷积层
二维卷积层将输入和卷积核做互相关运算,并加上一个标量偏差来得到输出。卷积层的模型参数包括了卷积核和标量偏差。在训练模型的时候,通常我们先对卷积核随机初始化,然后不断迭代卷积核和偏差。
卷积窗口形状为 p × q p \times q p×q 的卷积层称为 p × q p \times q p×q 卷积层。同样, p × q p \times q p×q 卷积或 p × q p \times q p×q 卷积核说明卷积核的高和宽分别为 p p p 和 q q q。
(1)填充可以增加输出的高和宽。这常用来使输出与输入具有相同的高和宽。
(2)步幅可以减小输出的高和宽,例如输出的高和宽仅为输⼊入的高和宽的 ( 为大于1的整数)。
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 11:20:57 2021
@author: 86493
"""
import torch
from torch import nn
# 卷积运算(二维互相关)
def corr2d(X, K):
h, w = K.shape
X, K = X.float(), K.float()
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (x[i: i + h, j: j + w] * K).sum()
return Y
# 二维卷积层
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super(Conv2D, self).__init__()
self.weight = nn.Parameter(torch.randn(kernel_size))
self.bias = nn.Parameter(torch.randn(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
conv2d = nn.Conv2d(in_channels = 1,
out_channels = 1,
kernel_size = 3,
padding = 1)
print(conv2d)
得:
Conv2d(1, 1, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
填充(padding)是指在输入高和宽的两侧填充元素(通常是0元素)。
下个栗子:创建一个高和宽为3的二维卷积层,设输入高和宽两侧的填充数分别为1。给定一高和宽都为8的input,输出的高和宽会也是8。
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 11:54:29 2021
@author: 86493
"""
import torch
from torch import nn
# 定义一个函数计算卷积层
# 对输入和输出左对应的升维和降维
def comp_conv2d(conv2d, X):
# (1, 1)代表批量大小和通道数
X = X.view((1, 1) + X.shape)
Y = conv2d(X)
# 排除不关心的前2维:批量和通道
return Y.view(Y.shape[2:])
# 注意这里是两侧分别填充1行或列,所以在两侧共填充2行或列
conv2d = nn.Conv2d(in_channels = 1,
out_channels = 1,
kernel_size = 3,
padding = 1)
X = torch.rand(8, 8)
endshape = comp_conv2d(conv2d, X).shape
print(endshape)
# 使用高为5,宽为3的卷积核,在高和宽两侧填充数为2和1
conv2d = nn.Conv2d(in_channels = 1,
out_channels = 1,
kernel_size = (5, 3),
padding = (2, 1))
endshape2 = comp_conv2d(conv2d, X).shape
print(endshape2)
结果为:
torch.Size([8, 8])
torch.Size([8, 8])
stride
在二维互相关运算中,卷积窗口从输入数组的最左上方开始,按从左往右、从上往下 的顺序,依次在输⼊数组上滑动。我们将每次滑动的行数和列数称为步幅(stride)。
# 步幅stride
conv2d = nn.Conv2d(in_channels = 1,
out_channels = 1,
kernel_size = (3, 5),
padding = (0, 1),
stride = (3, 4))
endshape3 = comp_conv2d(conv2d, X).shape
print(endshape3)
# torch.Size([2, 2])
2.4 池化层
- 池化层每次对输入数据的一个固定形状窗口(又称池化窗口)中的元素计算输出。不同于卷积层里计算输入和核的互相关性,池化层直接计算池化窗口内元素的最大值或者平均值。该运算也 分别叫做最大池化或平均池化。
- 在二维最大池化中,池化窗口从输入数组的最左上方开始,按从左往右、从上往下的顺序,依次在输入数组上滑动。当池化窗口滑动到某⼀位置时,窗口中的输入子数组的最大值即输出数组中相应位置的元素。
下面把池化层的前向计算实现在pool2d函数里。
最大池化:
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 18:49:27 2021
@author: 86493
"""
import torch
from torch import nn
def pool2d(x, pool_size, mode = 'max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
X = torch.Tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
end = pool2d(X, (2, 2)) # 默认是最大池化
# end = pool2d(X, (2, 2), mode = 'avg')
print(end)
tensor([[4., 5.],
[7., 8.]])
平均池化:
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 18:49:27 2021
@author: 86493
"""
import torch
from torch import nn
def pool2d(x, pool_size, mode = 'max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y
X = torch.FloatTensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
# end = pool2d(X, (2, 2)) # 默认是最大池化
end = pool2d(X, (2, 2), mode = 'avg')
print(end)
结果如下,注意上面如果mode是avg模式(平均池化)时,不能写X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]]),否则会报错Can only calculate the mean of floating types. Got Long instead.。把tensor改成Tensor或FloatTensor后就可以了(Tensor是FloatTensor的缩写)。
tensor([[2., 3.],
[5., 6.]])
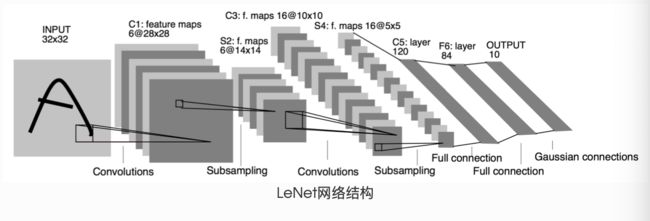
三、LeNet模型栗子
一个神经网络的典型训练过程如下:
1 定义包含一些可学习参数(或者叫权重)的神经网络
2. 在输入数据集上迭代
3. 通过网络处理输入
4. 计算 loss (输出和正确答案的距离)
5. 将梯度反向传播给网络的参数
6. 更新网络的权重,一般使用一个简单的规则:weight = weight - learning_rate * gradient
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 19:21:19 2021
@author: 86493
"""
import torch
import torch.nn as nn
import torch.nn.functional as F
class LeNet(nn.Module):
# 需要把网络中具有可学习参数的层放在构造函数__init__
def __init__(self):
super(LeNet, self).__init__()
# 输入图像channel:1;输出channel:6
# 5*5卷积核
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation:y = Wx + b
self.fc1 = nn.Linear(16 * 5 * 5, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 2 * 2 最大池化
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# 如果是方阵,则可以只使用一个数字进行定义
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
# 做一次flatten
x = x.view(-1, self.num_flat_features(x))
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def num_flat_features(self, x):
# 除去批处理维度,得到其他所有维度
size = x.size()[1:]
num_features = 1
# 将刚才得到的维度之间相乘起来
for s in size:
num_features *= s
return num_features
net = LeNet()
print(net)
# 一个模型的可学习参数可以通过`net.parameters()`返回
params = list(net.parameters())
print("params的len:", len(params))
# print("params:\n", params)
print(params[0].size()) # conv1的权重
print('-' * 60)
# 随机一个32×32的input
input = torch.randn(1, 1, 32, 32)
out = net(input)
print("网络的output为:", out)
print('-' * 60)
# 随机梯度的反向传播
net.zero_grad() # 清零所有参数的梯度缓存
end = out.backward(torch.randn(1, 10))
print(end) # None
print的结果为:
LeNet(
(conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=84, bias=True)
(fc3): Linear(in_features=84, out_features=10, bias=True)
)
params的len: 10
torch.Size([6, 1, 5, 5])
------------------------------------------------------------
网络的output为: tensor([[ 0.0904, 0.0866, 0.0851, -0.0176, 0.0198, 0.0530, 0.0815, 0.0284,
-0.0216, -0.0425]], grad_fn=)
------------------------------------------------------------
None
三点提醒:
(1)只需要定义 forward 函数,backward函数会在使用autograd时自动定义,backward函数用来计算导数。我们可以在 forward 函数中使用任何针对张量的操作和计算。
(2)在backward前最好net.zero_grad(),即清零所有参数的梯度缓存。
(3)torch.nn只支持小批量处理 (mini-batches)。整个 torch.nn 包只支持小批量样本的输入,不支持单个样本的输入。比如,nn.Conv2d 接受一个4维的张量,即nSamples x nChannels x Height x Width如果是一个单独的样本,只需要使用input.unsqueeze(0) 来添加一个“假的”批大小维度。
torch.Tensor:一个多维数组,支持诸如backward()等的自动求导操作,同时也保存了张量的梯度。nn.Module:神经网络模块。是一种方便封装参数的方式,具有将参数移动到GPU、导出、加载等功能。nn.Parameter:张量的一种,当它作为一个属性分配给一个Module时,它会被自动注册为一个参数。autograd.Function:实现了自动求导前向和反向传播的定义,每个Tensor至少创建一个Function节点,该节点连接到创建Tensor的函数并对其历史进行编码。
四、AlexNet模型栗子
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 16 21:00:39 2021
@author: 86493
"""
import torch
from torch import nn
class AlexNet(nn.Module):
def __init__(self):
super(AlexNet, self).__init__()
self.conv = nn.Sequential(
# in_channels,out_channels,kernel_size,stride,padding
nn.Conv2d(1, 96, 11, 4),
nn.ReLU(),
# kernel_size, stride
nn.MaxPool2d(3, 2),
# 见笑卷积窗口,但使用padding=2来使输入和输出的高宽相同
# 且增大输出通道数
nn.Conv2d(96, 256, 5, 1, 2),
nn.ReLU(),
nn.MaxPool2d(3, 2),
# 连续3个卷积层,且后面使用更小的卷积窗口
# 除了最后的卷积层外,进一步增大了输出
# 注:前2个卷积层后不使用池化层来减少输入的高和宽
nn.Conv2d(256, 384, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 383, 3, 1, 1),
nn.ReLU(),
nn.Conv2d(384, 256, 3, 1, 1),
nn.ReLU(),
nn.MaxPool2d(3, 2)
)
# 这里的全连接层的输出个数比LeNet中的大数倍。
# 使用丢弃层来缓解过拟合
self.fc = nn.Sequential(
nn.Linear(256 *5 * 5, 4096),
nn.ReLU(),
nn.Dropout(0.5),
nn.Linear(4096, 4086),
nn.ReLU(),
nn.Dropout(0.5),
# 输出层,下次会用到Fash-MNIST,所以此处类别设为10,
# 而非论文中的1000
nn.Linear(4096, 10),
)
def forward(self, img):
feature = self.conv(img)
output = self.fc(feature.view(img.shape[0], -1))
return output
net = AlexNet()
print(net)
可以看到该网络的结构:
AlexNet(
(conv): Sequential(
(0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))
(1): ReLU()
(2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(3): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
(4): ReLU()
(5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
(6): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(7): ReLU()
(8): Conv2d(384, 383, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(9): ReLU()
(10): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
(11): ReLU()
(12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
)
(fc): Sequential(
(0): Linear(in_features=6400, out_features=4096, bias=True)
(1): ReLU()
(2): Dropout(p=0.5, inplace=False)
(3): Linear(in_features=4096, out_features=4086, bias=True)
(4): ReLU()
(5): Dropout(p=0.5, inplace=False)
(6): Linear(in_features=4096, out_features=10, bias=True)
)
)
Reference
(1)官方文档:https://pytorch.org/docs/stable/_modules/torch/nn/modules/conv.html#Conv2d
(2)datawhale notebook
到此这篇关于PyTorch零基础入门之构建模型基础的文章就介绍到这了,更多相关PyTorch 构建模型基础内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!