最优化方法小结

线性搜索方法

梯度下降

在我的文章深度学习中常见的优化器小结中已经提到梯度下降法，这里，将重要的部分提炼过来。

其计算方法是：
给定待优化模型参数$\theta \in R^d$和目标函数$J(\theta )$后，算法沿着梯度的相反方向更新$\theta$来最小化$J(\theta )$。学习率$\eta$决定了每一时刻的更新步长。对于每一时刻t用以下步骤来说明梯度下降的流程：
（1）计算目标函数关于参数的梯度$g_t={\nabla }_{\theta }J(\theta )$

（2）更新模型参数
$${\theta }_{t+1}=\theta -\eta g_t$$

梯度下降与一阶泰勒展开：
假设损失函数是$J(\theta )$，对其做一阶泰勒展开：
$$J(\theta )=J({\theta }_0)+(\theta -{\theta }_0){\nabla }_{\theta }J({\theta }_0)$$
假设，$\theta -{\theta }_0=\lambda d$,其中$d$是方向向量，$\lambda$为标量，描述其长度。不难得出：
$(\theta -{\theta }_0){\nabla }_{\theta }J({\theta }_0)=\lambda |d||{\nabla }_{\theta }J({\theta }_0)|cos(\alpha )$，这里的$\alpha$是两个向量的夹角。如果我们期望梯度下降的方向最大，那么易知，$d$与梯度是反向的，则：$d=\frac{-{\nabla }_{\theta }J({\theta }_0)}{||{\nabla }_{\theta }J({\theta }_0)||}$。
那么，我们有：
$$\begin{gathered} \theta -{\theta }_0=\lambda d=\lambda \frac{-{\nabla }_{\theta }J({\theta }_0)}{||{\nabla }_{\theta }J({\theta }_0)||} \\ \theta ={\theta }_0-\frac{\lambda }{||{\nabla }_{\theta }J({\theta }_0)||}{\nabla }_{\theta }J({\theta }_0) \end{gathered}$$
也就得到了梯度下降的公式。

牛顿法

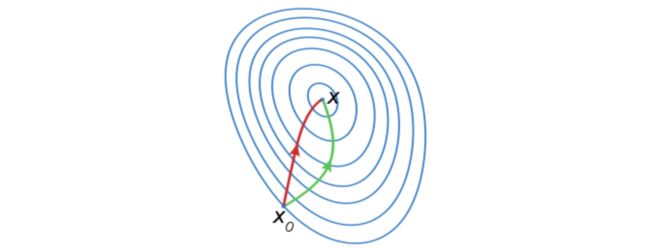
红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。
从几何的角度出发，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

牛顿法是怎么推导出来的呢？之前做梯度下降的时候我们对其进行了泰勒一阶展开，那么这里我们对其进行二阶展开，可得：
$$J(\theta )=J({\theta }_0)+(\theta -{\theta }_0){\nabla }_{\theta }J({\theta }_0)+\frac{1}{2}(\theta -{\theta }_0{)}^{T}H({\theta }_0)(\theta -{\theta }_0)$$
我们想要在$\theta$处取得极值点，那么只需要${\nabla }_{\theta }J(\theta )=0$，于是我们对上式求导，易得：
$${\nabla }_{\theta }J(\theta )={\nabla }_{\theta }J({\theta }_0)+H({\theta }_0)(\theta -{\theta }_0)=0$$
有：
$${\theta }_{t+1}={\theta }_t-H_t^{-1}{g}_t$$

这就是牛顿法。

拟牛顿法

我们知道求解海瑟矩阵的逆是一个非常复杂的计算，考虑使用一个n阶矩阵 $G$ 替代 $H^{-1}$ , 这就是拟牛顿法。

条件1：G 需要满足正定矩阵：
从牛顿法可知：
$${\theta }_{t+1}={\theta }_t-H_t^{-1}{g}_t$$
其实会在其中再增加一个学习率，也就是：
$$\begin{gathered} {\theta }_{t+1}={\theta }_t-\lambda H_t^{-1}{g}_t \\ {\theta }_{t+1}-{\theta }_t=-\lambda H_t^{-1}{g}_t \end{gathered}$$
带入到一阶泰勒展开式中，我们有：
$$J(\theta )=J({\theta }_0)-\lambda g_t^T{H}_t^{-1}{g}_t$$
因为$H^{-1}$正定，所以，$g_t^T{H}_t^{-1}{g}_t>0$。易知$J(\theta )<J({\theta }_0)$。
那么，要有一个$G$去拟合$H^{-1}$，显然，他需要是正定的

条件2：
显然，只有一个正定条件是不行的，首先牛顿法满足这样的性质：
$$\begin{gathered} {\nabla }_{\theta }J(\theta )={\nabla }_{\theta }J({\theta }_0)+H({\theta }_0)(\theta -{\theta }_0) \\ \Rightarrow g_{t+1}=g_t+H_t({\theta }_{t+1}-{\theta }_t) \\ \Rightarrow g_{t+1}-g_t=H_t({\theta }_{t+1}-{\theta }_t) \end{gathered}$$
令$y_t=g_{t+1}-g_t,{\delta }_t={\theta }_{t+1}-{\theta }_t$
$$\begin{gathered} y_t=H_t{\delta }_t \\ \Rightarrow H_t^{-1}{y}_t={\delta }_t \end{gathered}$$
成为拟牛顿条件，因此$G_t$需要满足这样的拟牛顿条件，则有：
$$G_t{y}_t={\delta }_t$$
我们希望有$G_{t+1}=G_t+\Delta G_t$。有以下两种算法：
DFP(Davidon-Fletcher-Powell)算法(DFP algorithm)

BFGS(Broyden-Fletcher-Goldfard-Shano)算法(BFGS algorithm)：

置信域方法

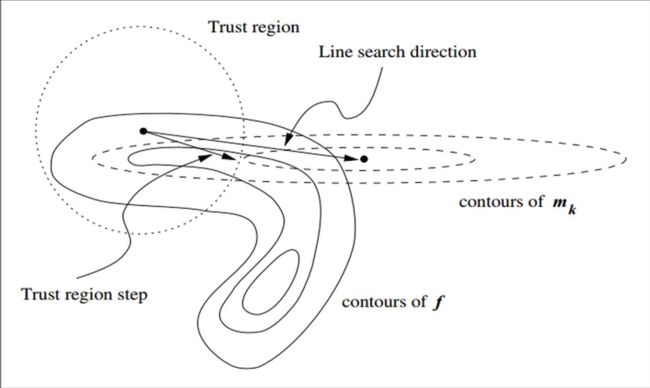
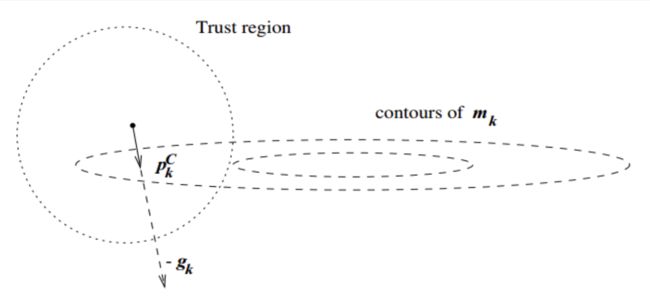
在信赖域方法的每次迭代中，先确定一个信赖域半径，然后在该半径内计算目标函数的二阶近似的极小值。如果该极小值使得目标函数取得了充分的下降，则进入下一个迭代，并扩大信赖域半径，如果该极小值不能令目标函数取得充分的下降，则说明当前信赖域区域内的二阶近似不够可靠，需要缩小信赖域半径，重新计算极小值。如此迭代下去，直到满足收敛所需的条件。我们结合上图做进一步的解释。

图中，实线表示的是目标函数的等高线，虚线是泰勒二阶近似的等高线：

因为泰勒二阶近似并不与目标函数完全相同，后面还有个高阶无穷小的值，因此他们的等高线不相同。如果我们使用牛顿法，那么他就会走到$m_k(p)$的极值点。但从图中不难看出，这个点根本没有充分的下降，在信頼域内最好的步骤是Trust region step，这个点比牛顿法的结果要好很多（在该例下）。

不过，这一现象比较依赖于信赖域半径的选取。可以想象，如果信赖域半径非常大，我们仍然会找到 $m_k(p)$ 的极小值点，但此时，这一步长是不能接受的，我们不会进入下一次迭代，而是要重新设置信赖域半径，重新计算步长。那么步长是否可接受的条件是什么呢？定义变量

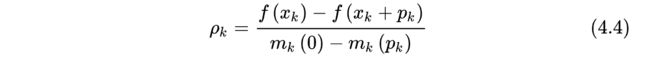
分母表示目标函数的二阶近似的减小量，分子表示目标函数的减小量。如果结果接近于1，说明二阶近似很接近目标函数，这一步长是可以接受的。如果结果接近于0甚至小于0，说明二阶近似与真实的目标函数差距较大，我们需要减小信赖域半径，并重新计算步长。

那么，问题只剩下，如何找到$m_k(p)$的极小值，这里只介绍Cauchy Point这一种方案，对Dogleg感兴趣的同学可以看信頼域这篇文章。

柯西点（Cauchy Point）：
这是一种近似求解的方法，固定$p$方向是梯度下降的方向，沿着这个方向寻找极小值，有：

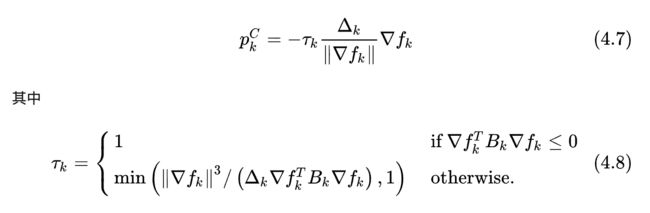
可以看出，步长为${\tau }_k{\Delta }_k$，方向为负梯度方向。至于${\tau }_k$的来源，可以直接将4.7的结果带入4.3


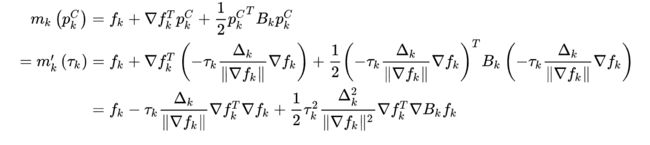
下面展示这种方法在例子中的效果：

启发式算法

在我的博文启发式算法中已经详细的介绍了相关算法，这里就不再赘述。

参考资料

梯度下降与一阶泰勒展开的关系
李航：《统计学习方法》，清华大学出版社
梯度下降法、牛顿法和拟牛顿法
信頼域