2021年华为杯数模赛D题总结
2021年华为杯数模赛D题总结
题目:
题目太长(网上能找到完整题目),背景信息略过,这里把题目抽象一下:
已有条件:
- 给出了1974个训练样本和50个测试样本,每个样本有729个特征
- 每个训练样本有7个标签,分别是IC50值、pIC50值、和ADMET性质(包含5个标签)
- IC50值、pIC50值是两个相关的连续变量。pIC50是IC50的负对数
- ADMET性质的五个变标签都是布尔值
问题:
- 根据特征对IC50值和pIC50值影响的重要性进行排序,并给出前20个对IC50值和pIC50值最具有显著影响的特征
- 选择不超过20个特征,构建IC50值和pIC50值的定量预测模型,并计算测试样本的IC50值和pIC50值。
- 构建ADMET性质的分类预测模型,并计算测试样本的ADMET性质
- 寻找并阐述哪些特征,以及这些特征在什么取值范围时,pIC50值取值较好,同时具有更好的ADMET性质(给定的五个ADMET性质中,至少三个性质较好)
把题目抽象以后,可以发现是一个很明显的利用机器学习模型处理数据挖掘的问题。题目的大致思路就出来了:
第一问主要问题:特征选择问题
第二问主要问题:回归预测问题
第三问主要问题:二分类问题
第四问主要问题:最优化问题
在使用机器学习模型之前,为简化模型,需要对题目做一些假设:
- 729个特征符合独立同分布
- 729个特征的值是准确可靠的
- ADMET与IC50值和pIC50值是相互独立的
不得不说,这个题目出得相当好。把数据挖掘的每个步骤都考到了,兼顾了回归问题和分类问题。用到的技术及要求比较全面,但又不过分深入。是一道很有价值的题目。
第一问
步骤一
根据假设2,数据集中没有脏数据。可略过数据清洗,直接进行特征选择。
特征可以分为三类,:
- 相关特征(保留):对于学习任务(例如分类问题)有帮助,可以提升学习算法的效果;
- 无关特征(剔除):对于我们的算法没有任何帮助,不会给算法的效果带来任何提升;
- 冗余特征(剔除):不会对我们的算法带来新的信息,或者这种特征的信息可以由其他的特征推断出;
根据假设1,数据集中不存在冗余特征,我们只需将无关特征剔除即可,首先要把方差极小的特征删除。
1.数据归一化(去量纲),保留原有特征分布。 n o r m ( x ) = x − m i n ( x ) m a x ( x ) − m i n ( x ) norm(x) = \frac{x-min(x)}{max(x)-min(x)} norm(x)=max(x)−min(x)x−min(x)
2.方差过滤,剔除方差较小的特征。
根据以上操作,剔除了568个无效的特征,剩余161个特征。
步骤二
这一步,我们使用了三种不同的方法进行特征选择分别是:
- 灰色关联分析(GRA)
- 递归特征消除(RFE)
- 互信息法(MIR)
为什么选择这三种方法呢?首先,我们分析数据之后,没能得出数据有什么特点,因此不知道什么样的特征选择方法是最优的。使用多种特征选择方法,之后再对比这几种方法的性能,总能选出一个最优的。其次,我们选择的方法既包含能表征线性关系的方法(GRA),有包含能表征非线性关系的方法(RFE/MIR)。
1.GRA:
GRA的原理和代码可参考我的博客:灰色关联分析
2.RFE:
递归特征消除的主要思想是反复的构建回归模型(这里用的是SVM),然后选出最好的(或者最差的)的特征。把选出来的特征剔除,然后在剩余的特征上重复这个过程,直到所有特征都遍历了。这个过程中特征被消除的次序就是特征的排序。
from sklearn.svm import SVC
from sklearn.feature_selection import RFE
svc = SVC(kernel="linear", C=1)
rfe = RFE(estimator=svc, n_features_to_select=1, step=1)
rfe.fit(X, y)
ranking = rfe.ranking_.reshape(digits.images[0].shape)
3.MIR:
MIR使用了概率论和信息论的知识。篇幅限制,我就贴一个总结的较好的博文吧:MIR
from sklearn.feature_selection import mutual_info_classif as MIC
result = MIC(X_fsvar,y)
k = result.shape[0] - sum(result <= 0)
X_fsmic = SelectKBest(MIC, k=20).fit_transform(X_fsvar, y)
cross_val_score(RFC(n_estimators=10,random_state=0),X_fsmic,y,cv=5).mean()
根据以上三种方法,我们得到了三组对pIC50影响最大的20个特征。那么该选那一组作为最终结果呢?我们将这三组特征使用第二问的模型进行对比,哪组拟合优度最好就选哪组。
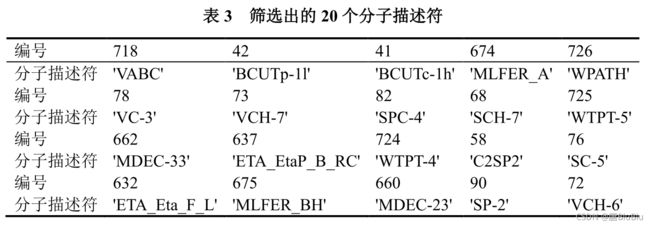
在这先放个最终答案吧(刚发现,这个三线表的格式有问题… 猛男哭哭):
第二问
我们使用了很多模型进行试验,包括SVM、线性回归、手工设计的全连接神经网络和matlab工具箱中的BP神经网络。这个过程就不再赘述了。最终结论就是matlab工具箱中的BP神经网络是效果最佳的。
BP神经网络的原理和实现方法参见我的博客:BP神经网络
我们得到的结果如下:
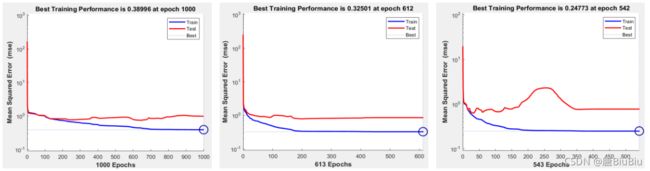
GAR/RFE/MIR的迭代曲线:
可见MIR的拟合优度最高。因此第一问最终结果就是使用MIR得到的那组特征。
下面拟合的pIC值与真实的pIC50值的对比:
赛后思考:这一问其实是有点问题的。RFE做特征选择的时候使用的模型是SVM,但实际性能对比的时候用到模型是BP神经网络,这是错误的。当选用BP神经网络时,我们应该让RFE使用BP神经网络重新做一次特征选择,这样才能保证结果是可靠的。
第三问
由假设3可知,第三问与前两问一毛钱关系都没有。
第三问是一个经典的二分类问题,套路与前两问类似——先做特征选择,再做预测模型。而随机森林算法既可以做二分类模型,也可以进行特征选择,因此这一问我们很自然的选择了随机森林算法。
随机森林是一种基于决策树的集成学习算法,具体的原理可以参考这篇博文:随机森林(by the way, 这篇文章详略得当,写的确实不错)
特征选择:
import sklearn.feature_selection
from sklearn.model_selection import ShuffleSplit
from collections import defaultdict
from sklearn.ensemble import RandomForestClassifier
rf = RandomForestClassifier(n_estimators=100,
criterion='gini',
verbose=1,
n_jobs=-1,
oob_score=True)
scores = defaultdict(list)
rs = ShuffleSplit(n_splits=5, test_size=0.2)
for train_idx, test_index in rs.split(x_train):
X_train, X_test = x_train[train_idx], x_train[test_index]
Y_train, Y_test = y[train_idx], y[test_index]
r = rf.fit(X_train,Y_train)
acc = mean_absolute_error(Y_test, rf.predict(X_test))
for i in range(x_train.shape[1]):
X_t = X_test.copy()
np.random.shuffle(X_t[:, i])
shuff_acc = mean_absolute_error(Y_test, rf.predict(X_t))
scores[i].append(abs(acc-shuff_acc))
print("Features sorted by their score:")
print(sorted([(round(np.mean(score), 4), feat) for
feat, score in scores.items()], reverse=True))
五个标签选择的特征分别是:
Caco-2 (相关性阈值取0.5): [719, 677, 105, 725, 716, 655, 626, 27, 26, 175, 8, 678, 653, 286, 630, 615, 605, 604, 594, 266, 66, 638, 35, 3, 720, 88, 294]
CYP3A4 (相关性阈值取0.5): [225, 105, 102, 100, 99, 722, 7, 91, 30, 623, 238, 98, 26, 653, 101, 346, 31]
hERG (相关性阈值取0.5): [357, 238, 476, 653, 606, 291, 4, 587, 480, 95, 92, 648, 11, 7, 410, 346, 250, 155, 104, 22, 8, 725, 647, 630, 84, 97]
HOB (相关性阈值取0.5): [39, 238, 119, 291, 357, 615, 44, 585, 346, 86, 292, 94, 23, 172, 465, 411, 630, 4, 606, 493, 476, 344, 228, 81, 619, 618, 594, 591, 529, 504, 225, 88, 610, 589, 587, 531, 463, 383, 237, 60]
MN (相关性阈值取0.3): [724,722,346]
分类预测:
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
X_train,X_test,Y_train,Y_test = train_test_split(x_train,y,test_size=0.2)
# 模型建立和训练
rf = RandomForestClassifier(
n_estimators=100,
criterion='gini',
verbose=1,
n_jobs=-1,
oob_score=True
)
rf.fit(X_train,Y_train)
predict = rf.predict(X_test)
# 模型评估
print('The accuracy of random forest classifier is', rf.score(X_test, Y_test))
print(classification_report(predict, Y_test))
# 预测
predict_test = rf.predict(x_test)
print('Final prediction result is:')
print(predict_test)
最终得到的结果为:
第四问
第四问是一个最优化问题,我们尝试了使用粒子群算法,但最后效果非常离谱。。总而言之,我们在第四问遇到了困难(猛男哭哭)。因此使用了一个非常不科学的方式:

这一部分我就不细讲了。最后贴个结果吧。
| 分子描述符序号 | 分子描述符 | 取值范围 |
|---|---|---|
| 68 | SCH-7 | (1.66 , +∞) |
| 73 | VCH-7 | (0.847 , +∞) |
| 78 | VC-3 | (2.46 , +∞) |
| 81 | VC-6 | (1.2, 1.25) |
| 90 | SP-2 | (18.481 , +∞) |
| 92 | SP-4 | (3.61 , +∞) |
| 346 | minwHBd | (-∞, 2.2) |
| 529 | maxssssNp | (1.2 , +∞) |
| 619 | ETA_BetaP_ns | (4.32 , +∞) |
| 665 | MDEO-11 | (8.91 , +∞) |
| 722 | WTPT-2 | (-∞, 9.2) |
| 724 | WTPT-4 | (-∞, 4.32) |
| 726 | WPATH | (30134.1 , +∞) |