原文链接:http://tecdat.cn/?p=24057
1.概要
本文的目标是使用各种预测模型预测Google的未来股价,然后分析各种模型。Google股票数据集是使用R中的Quantmod软件包从Yahoo Finance获得的。
2.简介
预测算法是一种试图根据过去和现在的数据预测未来值的过程。提取并准备此历史数据点,来尝试预测数据集所选变量的未来值。在市场历史期间,一直有一种持续的兴趣试图分析其趋势,行为和随机反应。不断关注在实际发生之前先了解发生了什么,这促使我们继续进行这项研究。我们还将尝试并了解 COVID-19对股票价格的影响。
3.所需包
library(quantmod) R的定量金融建模和交易框架
library(forecast) 预测时间序列和时间序列模型
library(tseries) 时间序列分析和计算金融。
library(timeseries) 'S4'类和金融时间序列的各种工具。
library(readxl) readxl包使你能够轻松地将数据从Excel中取出并输入R中。
library(kableExtra) 显示表格
library(data.table) 大数据的快速聚合
library(DT) 以更好的方式显示数据
library(tsfknn) 进行KNN回归预测4.数据准备
4.1导入数据
我们使用Quantmod软件包获取了Google股票价格2015年1月1日到2020年4月24日的数据,用于我们的分析。为了分析COVID-19对Google股票价格的影响,我们从quantmod数据包中获取了两组数据。
- 首先将其命名为data\_before\_covid,其中包含截至2020年2月28日的数据。
- 第二个名为data\_after\_covid,其中包含截至2020年4月24日的数据。
所有分析和模型都将在两个数据集上进行,以分析COVID-19的影响(如果有)。
getSymbols("GOG" fro= "2015-01-01", to = "2019-02-28")
before_covid <-dafae(GOOG)
getSymbols("GOG" , frm = "2015-01-01")
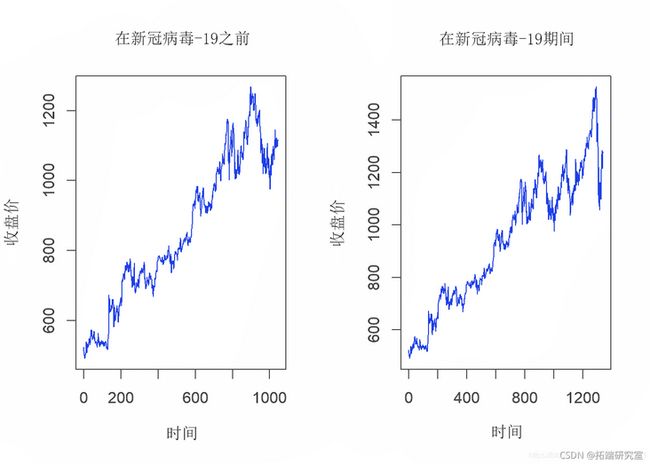
after_covid <- as.tae(GOOG)4.2数据的图形表示
par(mfrow = c(1,2))
plot.ts(fore_c)4.3数据集预览
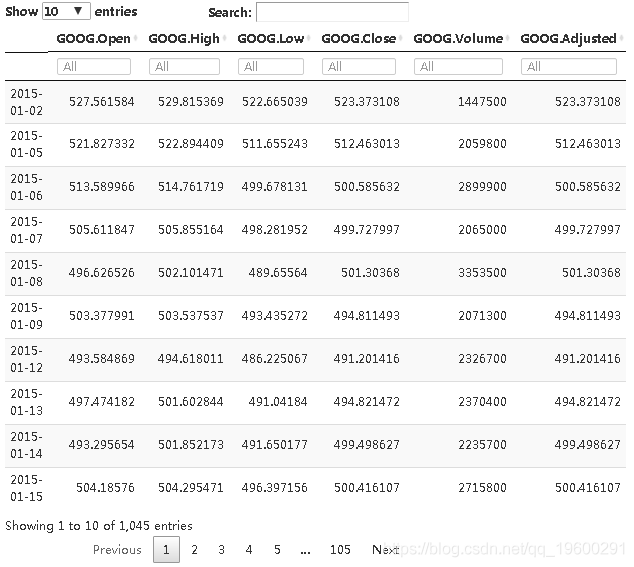
最终数据集可以在下面的交互式表格中找到。
table(before_covid)4.4变量汇总
变量
描述
Open
当日股票开盘价
High
当日股票最高价
Low
当日股价最低
Close
当日股票收盘价
Volumn
总交易量
Adjusted
调整后的股票价格,包括风险或策略
5. ARIMA模型
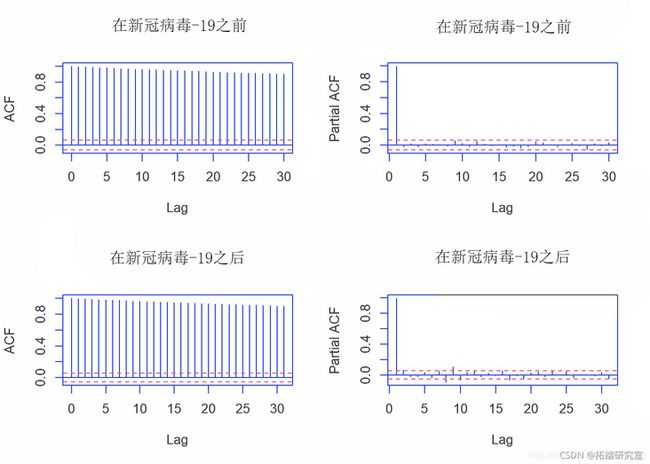
我们首先分析两个数据集的ACF和PACF图。
par(mfrow = c(2,2))
acft(bfoe_covid)
pacf(bfre_covid)然后,我们进行 ADF(Dickey-Fuller) 检验和 KPSS(Kwiatkowski-Phillips-Schmidt-Shin) 检验,检验两个数据集收盘价的时间序列数据的平稳性。
print(adf.test)print(adfes(sata\_after\_covid))通过以上ADF检验,我们可以得出以下结论:
- 对于COVID-19之前的数据集,ADF测试给出的p值为 0.2093,该值大于0.05,因此说明时间序列数据 不是平稳的。
- 对于COVID-19之后的数据集,ADF测试给出的p值为0.01974,该值 小于0.05,这说明时间序列数据是 平稳的。
print(kpss.s(t\_before\_covid))print(kpss.est(Dafter_covid))通过以上KPSS测试,我们可以得出以下结论:
- 对于COVID-19之前的数据集,KPSS测试得出的p值为 0.01,该值小于0.05,因此说明时间序列数据 不是平稳的。
- 对于COVID-19之后的数据集,KPSS测试给出的p值为 0.01,该值小于0.05,这说明时间序列数据 不是平稳的。
因此,我们可以从以上两个测试得出结论,时间序列数据 不是平稳的。
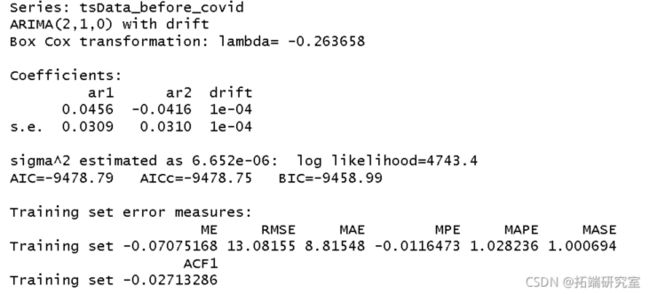
然后,我们使用 auto 函数来确定每个数据集的时间序列模型。
auto.ar(befor_covid, lamd = "auto") auto.arma(after_covid)从auto函数中,我们得出两个数据集的以下模型:
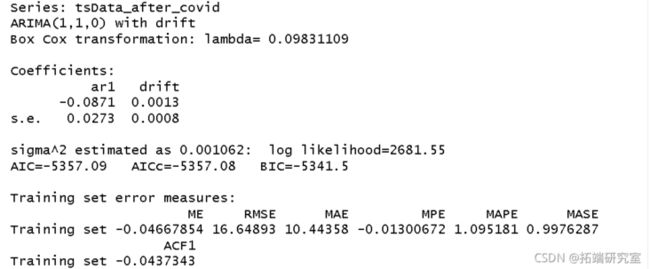
- 在COVID-19之前:ARIMA(2,1,0)
- 在COVID-19之后:ARIMA(1,1,1)
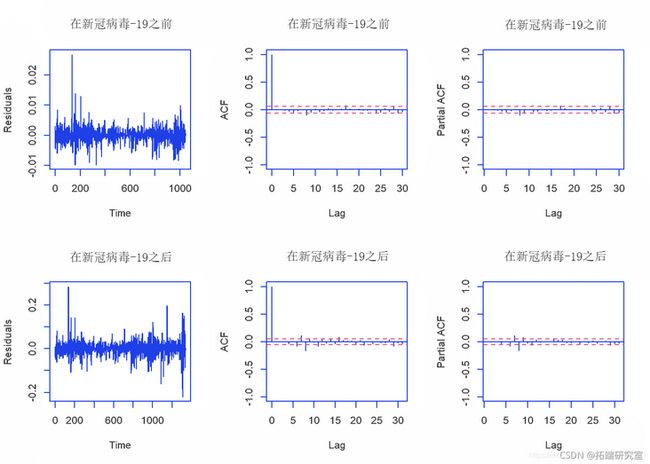
获得模型后,我们将对每个拟合模型执行残差诊断。
par(mfrow = c(2,3))
plot(before_covidresiduals)
plot(mfter_covidresiduals)从残差图中,我们可以确认残差的平均值为0,并且方差也为常数。对于滞后> 0,ACF为0,而PACF也为0。
因此,我们可以说残差表现得像白噪声,并得出结论:ARIMA(2,1,0)和ARIMA(1,1,1)模型很好地拟合了数据。或者,我们也可以使用Box-Ljung检验在0.05的显着性水平上进行检验残差是符合白噪声。
Box.test(moderesiduals)Box.tst(moeit\_fter\_covidreia, type = "Ljung-Box")在此,两个模型的p值均大于0.05。因此,在显着性水平为0.05的情况下,我们无法拒绝原假设,而得出的结论是残差遵循白噪声。这意味着该模型很好地拟合了数据。
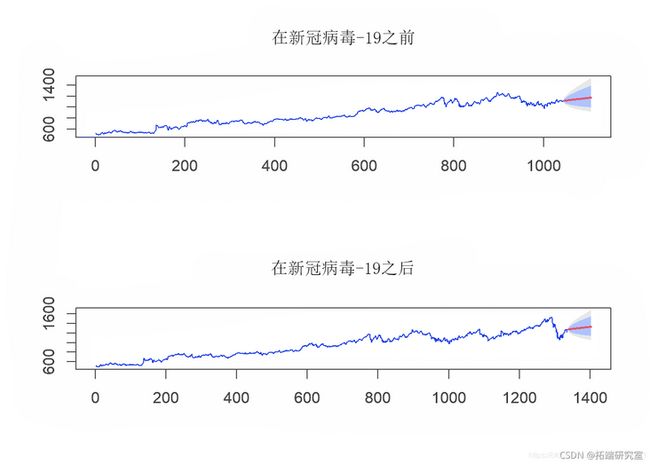
一旦为每个数据集确定了模型,就可以预测未来几天的股票价格。
6. KNN回归时间序列预测模型
KNN模型可用于分类和回归问题。最受欢迎的应用是将其用于分类问题。现在,使用r软件包,可以在任何回归任务应用KNN。这项研究的目的是说明不同的预测工具,对其进行比较并分析预测的行为。在我们的KNN研究之后,我们提出可以将其用于分类和回归问题。为了预测新数据点的值,模型使用“特征相似度”,根据新点与训练集上点的相似程度为值分配新点。
第一项任务是确定我们的KNN模型中的k值。选择k值的一般经验法则是取样本中数据点数的平方根。因此,对于COVID-19之前的数据集,我们取k = 32;对于COVID-19之后的数据集,我们取k = 36。
par(mfrow = c(2,1))
knn\_before\_covid <- kn(bfrvdGO.Clse, k = 32)
knn\_after\_covid <- kn(ber_oiGOG.lose ,k = 36)
plot(knn\_before\_covid )
plot(knn\_after\_covid )然后,我们针对预测时间序列评估KNN模型。
before\_cvid <- ll\_ig(pdn\_befr\_vid)
afer\_vd<- rog\_ogn(redkn\_afer\_vd)7.前馈神经网络建模
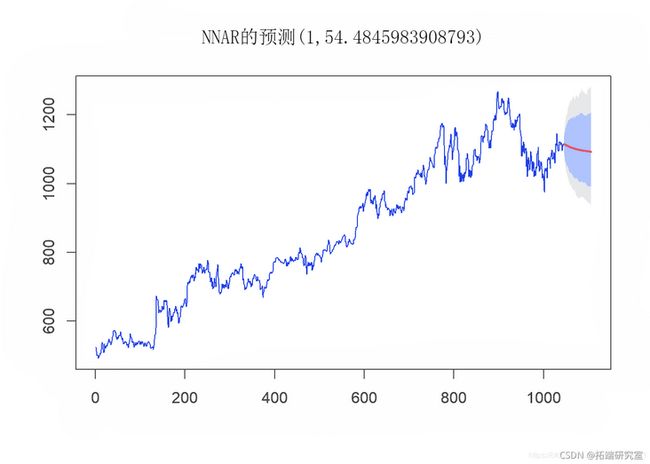
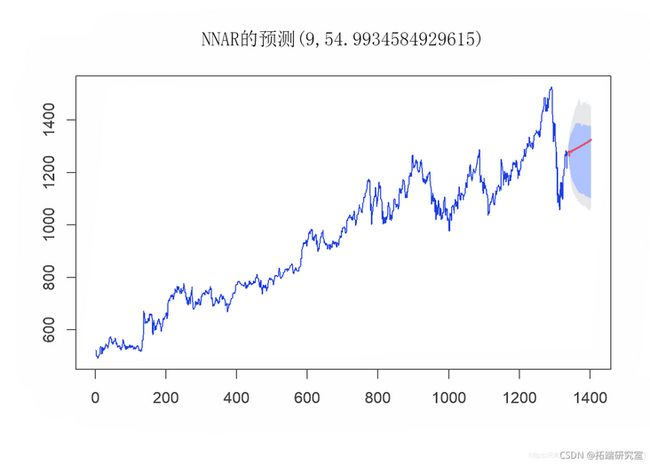
我们将尝试实现的下一个模型是带有神经网络的预测模型。在此模型中,我们使用单个隐藏层形式,其中只有一层输入节点将加权输入发送到接收节点的下一层。预测函数将单个隐藏层神经网络模型拟合到时间序列。函数模型方法是将时间序列的滞后值用作输入数据,以达到非线性自回归模型。
第一步是确定神经网络的隐藏层数。尽管没有用于计算隐藏层数的特定方法,但时间序列预测遵循的最常见方法是通过计算使用以下公式:
其中Ns:训练样本数Ni:输入神经元数No:输出神经元数a:1.5 ^ -10
#隐藏层的创建
hn\_before\_covid <- length(before.Close)/(alpha*(lengthGOOG.Close + 61)
hn\_after\_covid <- length(after\_covidClose)/(alpha*(lengthafter\_ovdClose+65))
#拟合nn
nn(before\_covid$GOOG.Close, size = hn\_beoe_cid,
# 使用nnetar进行预测。
forecast(befe_cvid, h 61, I =UE)
forecast(aftr_coid, h = 5, I = RE)plot(nn\_fcst\_afte_cvid)然后,我们使用以下参数分析神经网络模型的性能:
accuracyaccuracy8.所有模型的比较
现在,我们使用参数诸如RMSE(均方根误差),MAE(均值绝对误差)和MAPE(均值绝对百分比误差)对所有三个模型进行分析 。
sumary\_le\_efore_oid <- data.frame(RMSE = nuerc(), MAE = uer(),
MAPE = numric(), snsAsacrs = FALSE)
summ\_tabe\_fter_ovd <- data.fame(RMSE = umeri(), MAE = nmei(),
MAPE = numeic())
kable(smary\_abe\_eor_oid )COVID-19之前的数据模型汇总
模型
RMSE
MAE
MAPE
ARIMA
13.0
8.8
1.0
KNN
44.0
33.7
3.1
神经网络
13.0
8.7
1.0
kable(sumary\_tbl\_aft_ci
fulith = F, fixdtead = T )COVID-19之后的数据模型汇总
模型
RMSE
MAE
MAPE
ARIMA
16.6
10.4
1.0
KNN
45.9
35.7
3.3
神经网络
14.7
9.8
1.0
因此,从以上模型性能参数的总结中,我们可以看到神经网络模型在两个数据集上的性能均优于ARIMA和KNN模型。因此,我们将使用神经网络模型来预测未来两个月的股价。
9.最终模型:COVID-19之前
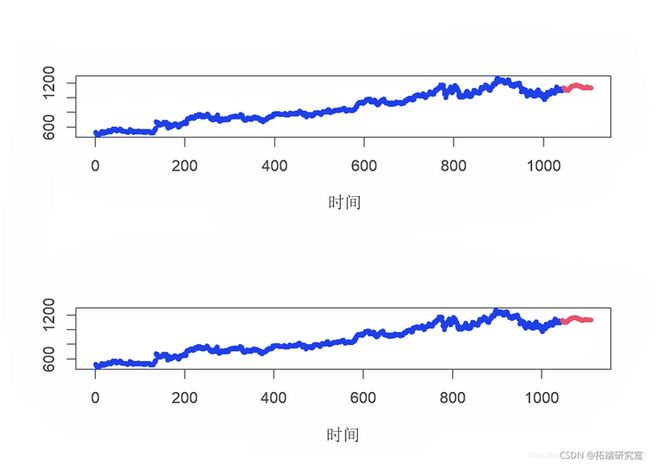
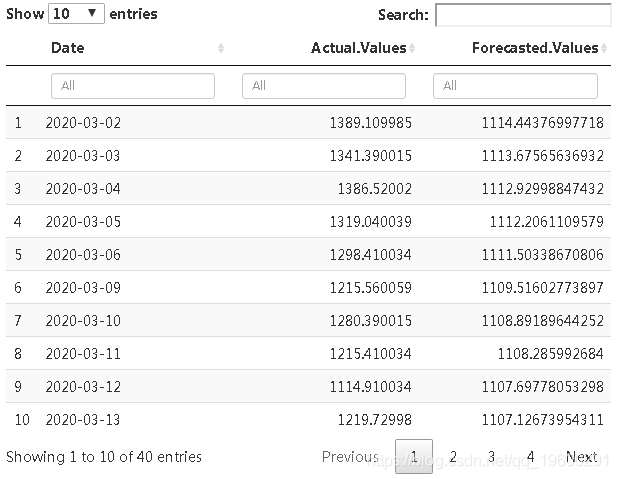
现在,我们使用直到2月的数据来预测3月和4月的值,然后将预测价格与实际价格进行比较,以检查是否由于COVID-19可以归因于任何重大影响。
foestdungcvid<- datafame("De
"Actua Values" =
datatable(foestdungcvid, ilte= 'to')从表中我们可以看到,3月和4月期间,Google股票的实际价值通常比预测值要高一些。因此,可以说,尽管发生了这种全球性大流行,但Google股票的表现仍然相当不错。
10.最终模型:COVID-19之后
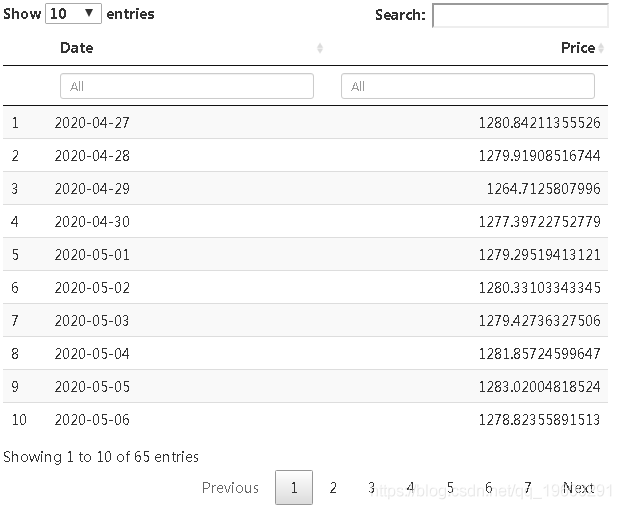
现在,我们使用直到4月的数据预测5月和6月的值,以了解Google的未来股价。
foreataov <- data.frae(dn_reataeimean )
table(foreataov )从表中可以得出结论,在5月和6月的接下来的几个月中,Google股票的价格将继续上涨并表现良好。
最受欢迎的见解
1.在python中使用lstm和pytorch进行时间序列预测
2.python中利用长短期记忆模型lstm进行时间序列预测分析