「手把手带你学算法」本周小结!(动态规划系列七)
相信很多小伙伴刷题的时候面对力扣上近两千道题目,感觉无从下手,我花费半年时间整理了Github项目:leetcode刷题攻略。 里面有100多道经典算法题目刷题顺序、配有40w字的详细图解,常用算法模板总结,以及难点视频讲解,按照list一道一道刷就可以了!star支持一波吧!
本周的主题就是股票系列,来一起回顾一下吧
周一
动态规划:买卖股票的最佳时机II中股票可以买买多了次!
这也是和121. 买卖股票的最佳时机的唯一区别(注意只有一只股票,所以再次购买前要出售掉之前的股票)
重点在于递推公式公式的不同。
在回顾一下dp数组的含义:
- dp[i][0] 表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
递推公式:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);
大家可以发现本题和121. 买卖股票的最佳时机的代码几乎一样,唯一的区别在:
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
这正是因为本题的股票可以买卖多次! 所以买入股票的时候,可能会有之前买卖的利润即:dp[i - 1][1],所以dp[i - 1][1] - prices[i]。
周二
动态规划:买卖股票的最佳时机III中最多只能完成两笔交易。
这意味着可以买卖一次,可以买卖两次,也可以不买卖。
- 确定dp数组以及下标的含义
一天一共就有五个状态,
0. 没有操作
- 第一次买入
- 第一次卖出
- 第二次买入
- 第二次卖出
dp[i][j]中 i表示第i天,j为 [0 - 4] 五个状态,dp[i][j]表示第i天状态j所剩最大现金。
- 确定递推公式
需要注意:dp[i][1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
- dp数组如何初始化
dp[0][0] = 0;
dp[0][1] = -prices[0];
dp[0][2] = 0;
dp[0][3] = -prices[0];
dp[0][4] = 0;
- 确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
- 举例推导dp数组
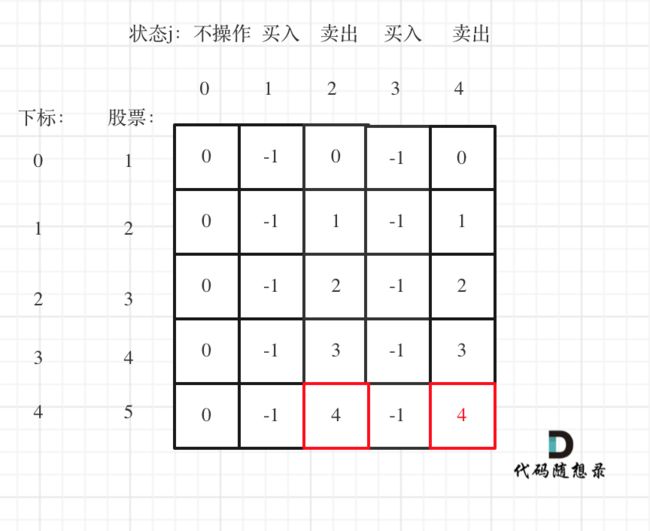
以输入[1,2,3,4,5]为例
可以看到红色框为最后两次卖出的状态。
现在最大的时候一定是卖出的状态,而两次卖出的状态现金最大一定是最后一次卖出。
所以最终最大利润是dp[4][4]
周三
动态规划:买卖股票的最佳时机IV最多可以完成 k 笔交易。
相对于上一道动态规划:123.买卖股票的最佳时机III,本题需要通过前两次的交易,来类比前k次的交易
- 确定dp数组以及下标的含义
使用二维数组 dp[i][j] :第i天的状态为j,所剩下的最大现金是dp[i][j]
j的状态表示为:
- 0 表示不操作
- 1 第一次买入
- 2 第一次卖出
- 3 第二次买入
- 4 第二次卖出
- …
除了0以外,偶数就是卖出,奇数就是买入。
- 确定递推公式
还要强调一下:dp[i][1],表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区。
for (int j = 0; j < 2 * k - 1; j += 2) {
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
}
本题和动态规划:123.买卖股票的最佳时机III最大的区别就是这里要类比j为奇数是买,偶数是卖剩的状态。
- dp数组如何初始化
dp[0][j]当j为奇数的时候都初始化为 -prices[0]
代码如下:
for (int j = 1; j < 2 * k; j += 2) {
dp[0][j] = -prices[0];
}
在初始化的地方同样要类比j为偶数是买、奇数是卖的状态。
- 确定遍历顺序
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
- 举例推导dp数组
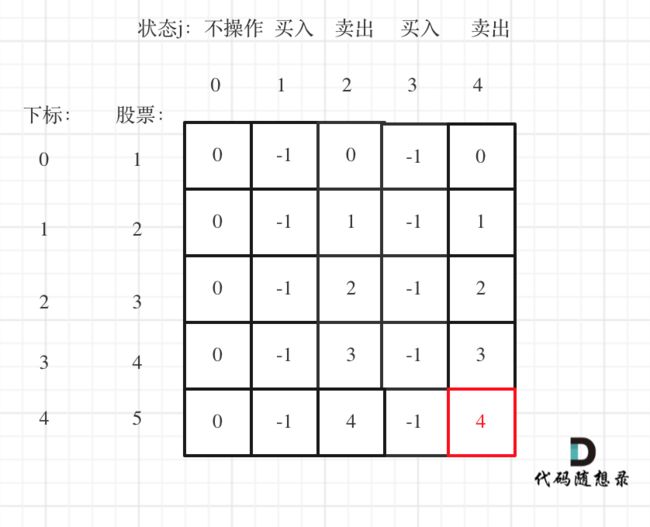
以输入[1,2,3,4,5],k=2为例。
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
周四
动态规划:最佳买卖股票时机含冷冻期尽可能地完成更多的交易(多次买卖一支股票),但有冷冻期,冷冻期为1天
相对于动态规划:122.买卖股票的最佳时机II,本题加上了一个冷冻期
本题则需要第三个状态:不持有股票(冷冻期)的最多现金。
动规五部曲,分析如下:
- 确定dp数组以及下标的含义
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
j的状态为:
- 1:持有股票后的最多现金
- 2:不持有股票(能购买)的最多现金
- 3:不持有股票(冷冻期)的最多现金
- 确定递推公式
dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]);
dp[i][1] = max(dp[i - 1][1], dp[i - 1][2]);
dp[i][2] = dp[i - 1][0] + prices[i];
- dp数组如何初始化
可以统一都初始为0了。
代码如下:
vector> dp(n, vector(3, 0));
初始化其实很有讲究,很多同学可能是稀里糊涂的全都初始化0,反正就可以通过,但没有想清楚,为什么都初始化为0。
- 确定遍历顺序
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历。
- 举例推导dp数组
以 [1,2,3,0,2] 为例,dp数组如下:
最后两个状态 不持有股票(能购买) 和 不持有股票(冷冻期)都有可能最后结果,取最大的。
总结
下周还会有一篇股票系列的文章,股票系列后面我也会单独写一篇总结,来高度概括一下,这样大家会对股票问题就有一个整体性的理解了。
我是程序员Carl,可以找我组队刷题,「代码随想录」目前正在循序渐进讲解算法,目前已经讲到了动态规划,点击这里和上万录友一起打卡学习!
我已经陆续将我的题解按照由浅入深的刷题顺序编排起来,整理成册,这份刷题顺序和题解在公众号里已经陪伴了上万录友。
PDF中不仅有刷题大纲、刷题顺序,还有详细图解,每一本PDF发布之后都广受好评,这也是Carl花费大量时间写题解的动力。
PDF部分截图:
说了这么多还是眼见为实,在『代码随想录』后台回复:pdf,就可以获得全部已经整理出来的pdf,赶快去看一看,你会发现相见恨晚!
如果感觉题解对你有帮助,不要吝啬给一个吧!