模式匹配算法
Pattern Matching
- 概念
-
- 朴素算法
- Hash 运算
- KMP 算法
概念
形如 Java 的 String.indexOf(String),C 的 strstr(char*, char*) 这类子串定位运算,可称为模式匹配。
模式匹配是字符串中一种基本运算。
具体的来讲,给定字符串 S 1 [ 1 ∼ n ] S_{1}[1 \sim n] S1[1∼n]、 S 2 [ 1 ∼ m ] S_{2}[1 \sim m] S2[1∼m],要求求出所有使得 S 1 [ i ∼ i + m ] = S 2 [ 1 ∼ m ] S_{1}[i \sim i + m] = S_{2}[1 \sim m] S1[i∼i+m]=S2[1∼m] 的 i i i, i ≤ n − m i \leq n - m i≤n−m,即子串匹配问题。
在模式匹配里 S 2 S_{2} S2 被称为模式 P P P, S 1 S_{1} S1 被称为目标 T T T,任务是在 T T T 中寻找若干 子串 P P P。
通常,我们只需求出最小的 i i i 即可。
为了方便接下来的实现,下标从0开始计算。
值得注意的是,当 P P P 为空串时,我们引用 Java 和 C 的做法,返回下标0。
模式串当然也可以多至 m m m 个,如果我们能在线性时间内处理完匹配,那么在 O ( n m ) O(nm) O(nm) 的复杂度下完成其实也是可以接受的,但可能会存在更好的方法,这里开个坑,不见得会填。
朴素算法
Brute Force
一种朴素的想法,就是我们拿出 T [ 1 ∼ n ] T[1 \sim n] T[1∼n] 的所有长度为 m m m 子串 T [ 1 ∼ m ] 、 T [ 2 ∼ m + 1 ] 、 . . . 、 T [ n − m ∼ n ] T[1 \sim m] 、 T[2 \sim m + 1] 、... \ \ 、T[n - m \sim n] T[1∼m]、T[2∼m+1]、... 、T[n−m∼n] 和 P [ 1 ∼ m ] P[1 \sim m] P[1∼m] 一一对比,暴力的搜索出子串开始下标,这种做法时间复杂度在 O ( m n ) 。 O(mn)。 O(mn)。
public int indexOf(String T, String P) {
int n = T.length(), m = P.length();
for (int i = 0; i <= n - m; i++) {
boolean flag = true;
for (int j = 0; j < m; j++)
if (T.charAt(i + j) != P.charAt(j))
flag = false;
if (flag) return i;
}
return -1;
}
这段代码里显然有一个可以做常数优化的点,这里留给不熟悉字符串的读者自行思考。
Hash 运算
嗯赌
对于一个字符串,我们只需要线性时间内的预处理,然后在常数时间内就能拿到其子串的 hash值,也就是整个匹配时间能在 O ( n ) O(n) O(n) 意义下完成。
如果 T T T 的子串 hash值 和 P P P 的不等,那么它们一定不等。
如果 T T T 的子串 hash值 和 P P P 的相等,但它们不一定相等。
与 Hash 有关的内容这里便不再展开来讲,
这里只提供一个使用 Hash 模式匹配的示例。
public final int p = 31;
public int indexOf(String T, String P) {
int n = T.length(), m = P.length();
long[] THash = new long[n + 1];
long PHash = 0, PPowM = 1;
for (int i = 0; i < m; i++) {
PPowM = PPowM * p;
PHash = PHash * p + P.charAt(i);
}
for (int i = 0; i < n; i++)
THash[i + 1] = THash[i] * p + T.charAt(i);
for (int i = m; i <= n; i++) {
long k = THash[i] - THash[i - m] * PPowM;
if (THash[i] - THash[i - m] * PPowM == PHash)
return i - m;
}
return -1;
}
发生 hash 碰撞后,可以改用其他质数,或调整为BF算法。
KMP 算法
Knuth-Morris-Pratt Algorithm
大的要来咯
首先定义前缀函数 f f f,以及其使用。
出于惯例我们使用整型数组next保存前缀函数的结果。
这里使用名词前缀函数是为了避免与后缀数组混淆,
也就是这里计算出的 “前缀数组” 并非和后缀数组相近的概念。
我们还需要了解非前缀子串的含义:
对于字符串 S [ 1 ∼ n ] S[1 \sim n] S[1∼n],它的非前缀子串有 { S [ i ∼ j ] ∣ 1 < i ≤ j ≤ n } \{ S[i \sim j] \ | \ 1 < i \leq j\leq n\} { S[i∼j] ∣ 1<i≤j≤n},也就是并非以字符串头开头的子串。
前缀函数 f ( i ) f(i) f(i) 的值为以第 i i i 个字符结尾的非前缀子串与原串的最大匹配长度。
出于惯例, f ( 1 ) f(1) f(1) 记做 − 1 -1 −1。
我们思考一下朴素匹配的过程,给定串 T T T、 P P P:
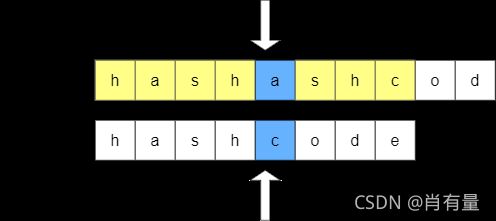
当匹配到 T [ 1 ∼ 8 ] T[1 \sim 8] T[1∼8] 比较到 P 5 P_{5} P5 时,匹配已经失败,
比较直接开始匹配下一个子串。

和顺序跳过已匹配距离 4 4 4 减去 f ( 4 ) f(4) f(4) 个待匹配子串。

当然现在已经匹配失败了,
但是到这里我们就能发现,
在匹配失败发生时,我们将 T T T 左 或 P P P 右 移 f ( 已 匹 配 距 离 ) f(已匹配距离) f(已匹配距离)个单位,最后的结果仍然是正确的。
也就是说在这之间 T T T 的子串绝对不可能和 P P P 相同。
严格来讲:
T [ k ∼ k + m ] T[k \sim k + m] T[k∼k+m] 与 P [ 1 ∼ m ] P[1 \sim m] P[1∼m] 的 [ 1 ∼ i − 1 ] [1 \sim i - 1] [1∼i−1] 处相同, i i i, i ≤ m i \leq m i≤m 处相异,则 T [ k + j ∼ k + m + j ] T[k + j \sim k + m + j] T[k+j∼k+m+j], j ∈ [ 0 , i − f ( x ) ) j \in [0,\ i - f(x)) j∈[0, i−f(x)) 必不可能与 P P P 相等。
因为 f ( i ) f(i) f(i) 是 P P P 以第 i i i 个字符结尾的非前缀子串与原串的最大匹配长度,
若存在 j 0 j_{0} j0, i > j 0 > f ( i ) i > j_{0} > f(i) i>j0>f(i)使得 T [ k + i − j 0 ∼ k + i ] = P [ 1 ∼ j 0 ] T[k + i - j_{0} \sim k + i] = P[1 \sim j_{0}] T[k+i−j0∼k+i]=P[1∼j0],这就意味着 j 0 j_{0} j0 可使 P [ 1 ∼ j 0 ] = P [ i − j 0 ∼ i ] P[1 \sim j_{0}] = P[i - j_{0} \sim i] P[1∼j0]=P[i−j0∼i],这与前缀函数匹配长度的最大性相悖。
也因此在 T [ k + j ∼ k + m + j ] T[k + j \sim k + m + j] T[k+j∼k+m+j] 中每个子串都与 P P P 的前缀相异,故必不可能与 P P P 相等。
我们先朴素的求出所有 f ( x ) f(x) f(x),将其保存到next数组里,随后还会安装上述这个性质对next的求法进行一定的优化,使其能在线性时间内完成。
public int indexOf(String T, String P) {
int n = T.length(), m = P.length();
int[] next = new int[m];
for (int i = 0; i < m; i++)
for (int j = 0; j < i; j++)
if (P.substring(0, j).equals(P.substring(i - j, i)))
next[i] = j;
for (int i = 0, j = 0; i < n;) {
if (j == 0) {
if (T.charAt(i) == P.charAt(j))
{
i++; j++; }
else i++;
} else if (T.charAt(i) == P.charAt(j))
{
i++; j++; }
else j = next[j];
if (j == m) return i - j;
}
return -1;
}
可以看到在这段程序中,处理next的复杂度为 O ( m 2 ) O(m^{2}) O(m2),整个查找过程中, j j j 的减少次数不会超过 j j j 的增加次数,故 j j j 的总变化次数至多为 2 ( n + m ) 2(n + m) 2(n+m),整个算法时间复杂度为 O ( n + m 2 ) O(n + m^{2}) O(n+m2)。
在 n n n 远远大于 m m m 时,这个复杂度显然可以接受,但是对于预处理next的过程,我们还有更好的方案。
从上面的证明中我们能推出,在 i i i 处发生匹配发生失败时,要使得 T T T 继续匹配,回退的位置只会从 f ( i ) , f ( f ( i ) ) , . . . , 0 f(i),\ f(f(i)),\ ... \ ,0 f(i), f(f(i)), ... ,0 即 next[i],next[next[i]],… ,0中产生。
那么把这段话的 T T T 替换成 P P P 呢?
首先要确定next[i]的能否从next[i - 1]中确定,要使 P [ k ∼ i ] = P [ 1 ∼ i − k ] P[k \sim i] = P[1 \sim i -k] P[k∼i]=P[1∼i−k]
算了我再重新写一份,写的太粪了。
等我有时间。