两个不规则四边形IOU计算方法
1 引言
我们常用的目标检测为矩形框检测,但是我们有时检测出来的框为不规则的四边形,如下图为常见的遥感图像,此时我们在使用矩形框计算IOU的方式就不再适用.我们可以将问题进行抽象,有木有计算两个不规则四边形IOU的计算方式呢?
2 矩形框IOU计算方式
一般来说,我们对目标矩形框的抽象有两种方式:
- 左上右下表示 : x1 y1 x2 y2
- 中心点表示: c_x,c_y,w,h
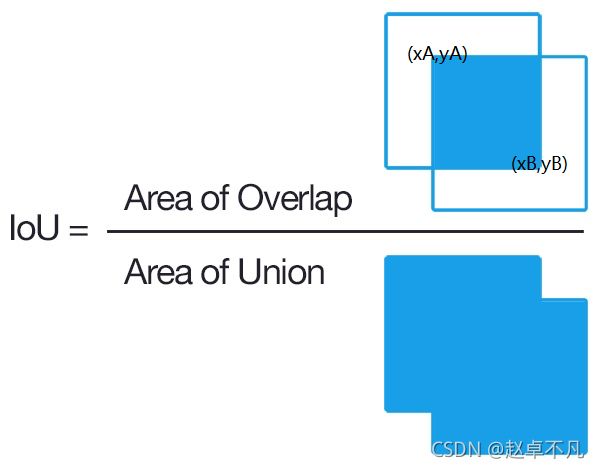
两种表示下的矩形框的IOU的计算方式如下:
def bb_intersection_over_union(boxA, boxB):
boxA = [int(x) for x in boxA]
boxB = [int(x) for x in boxB]
xA = max(boxA[0], boxB[0])
yA = max(boxA[1], boxB[1])
xB = min(boxA[2], boxB[2])
yB = min(boxA[3], boxB[3])
interArea = max(0, xB - xA + 1) * max(0, yB - yA + 1)
boxAArea = (boxA[2] - boxA[0] + 1) * (boxA[3] - boxA[1] + 1)
boxBArea = (boxB[2] - boxB[0] + 1) * (boxB[3] - boxB[1] + 1)
iou = interArea / float(boxAArea + boxBArea - interArea)
return iou
解释如下:
- 由于两个矩形框的交集依旧为矩形,所以我们首先计算交集矩形框的左上和右下坐标 xA,yA,xB,yB
- 计算两个矩形框交集矩形框的面积 interArea
- 利用两个矩形框并集=矩形框A的面积+矩形框B的面积-交集的面积可以得到两个矩形并集的面积
- 利用交集矩形面积除以并集矩形面积得到IOU即可
3 不规则四边形IOU计算方式
阅读上述矩形框IOU的计算方式,由于矩形框的交集依旧为矩形框,所以其交集矩形计算相对简单.接下来我们来思考不规则四边形IOU的计算方式:
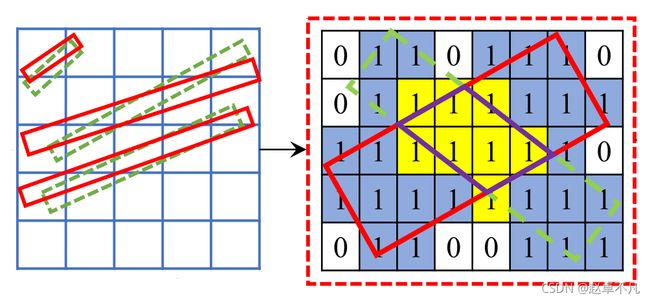
如上图右侧所示,红色实线框为标注的真值框,前绿色虚线框为预测框.
我们可以采用两个任意旋转框之间的共有像素个数来近似IoU,考虑到图像均为整形坐标,所以不规则四边形的面积可以用所包含的像素点个数来近似代替.
基于此,我们将任意两个不规则四边形的IOU计算步骤总结如下:
- step1: 生成三张全黑二值图( I A I_A IA , I B I_B IB , I C I_C IC ), 长和宽同网络输入
- step2: 将四边形 R e c t A Rect_A RectA 画到二值图 I A I_A IA 上 , 并进行全白填充,像素值填充为255
- step3: 将四边形 R e c t B Rect_B RectB 画到二值图 I B I_B IB 上, 并进行全白填充,像素值填充为255
- step4: 将四边形 R e c t A Rect_A RectA和 R e c t B Rect_B RectB 分别画到二值图 I C I_C IC 上, 并进行全白填充,像素值填充为255
- step5: 分别计算三张二值图 I A I_A IA, I B I_B IB, I C I_C IC上白色像素点个数,分别摆表示为 S u m A Sum_A SumA, S u m B Sum_B SumB, S u m C Sum_C SumC
- step6: 计算两个四边形的交集面积 A r e a 1 Area_1 Area1 = S u m A Sum_A SumA + S u m B Sum_B SumB - S u m C Sum_C SumC
- step6: 计算两个四边形的并集面积 A r e a 2 Area_2 Area2 = S u m C Sum_C SumC
- step7: 计算交并比 I o u Iou Iou = A r e a 1 Area_1 Area1 / A r e a 2 Area_2 Area2
上述计算流程如下图所示:
上图所示:
左上红色框为四边形的真值,绿色框为四边形的预测框.
右上所示为上述步骤2中所得到的真值框的填充图;
左下所示为上述步骤3中所得到的预测框的填充图;
右下所示为上述步骤4中所得到的预测框和真值框并集后的填充图.
4 代码实现
4.1 生成样例
我们假设我们网络输入为320X320,对应的真值框为rect1,对应的预测框为rect2,二者均为不规则的四边形,如下所示:
net_width = 320
net_height = 320
rect1 = [160,100, 120,220, 200,220, 180, 100]
rect2 = [180,150, 150,250, 220,250, 230 ,152]
4.2 填充函数
接下来需要对真值框和预测框进行填充,这里我们使用fillPoly函数完成上述功能,代码实现如下:
def draw_region(img,rect_1,rect_2=None,fill_value=255):
pt_list = list()
for i in range(4):
pt_list.append((rect_1[i*2],rect_1[i*2+1]))
cv2.fillPoly(img, [np.array(pt_list)], fill_value)
if rect_2 is not None:
pt_list2 = list()
for i in range(4):
pt_list2.append((rect_2[i * 2], rect_2[i * 2 + 1]))
cv2.fillPoly(img, [np.array(pt_list2)], fill_value)
return img
4.3 计算IOU
接下来我们统计三副填充后的图像的面积,进而可以计算真值框和预测框对应的交并比,代码实现如下:
def compute_iou(net_width,net_height,rect1,rect2,fill_value=255):
img1 = np.zeros((net_height, net_width), np.uint8)
img2 = np.zeros((net_height, net_width), np.uint8)
img3 = np.zeros((net_height, net_width), np.uint8)
out_img1 = draw_region(img1, rect1, fill_value=fill_value)
out_img2 = draw_region(img2, rect2, fill_value=fill_value)
out_img3 = draw_region(img3, rect1, rect2, fill_value=fill_value)
area_1 = np.sum(out_img1 == fill_value)
area_2 = np.sum(out_img2 == fill_value)
area_com = np.sum(out_img3 == fill_value)
print("area1 ={} area2={} area3={} ".format(area_1, area_2, area_com))
iou = (area_1 + area_2 - area_com) * 1.0 / area_com
return iou
运行结果如下:

通过上图可以得到样例中两个四边形的交并比为0.17.
4.4 应用
举了实际应用中的例子吧,如下图所示,我们左鱼眼图像上泊车位的检测,检出来的结果为不规则四边形,需要进行NMS保留置信度最高的检测框,此时就需要用到上述不规则四边形IOU的计算方式来进行NMS操作.
5 总结
本文从两个矩形框的交并比计算开始扩展到两个不规则四边形交并比的计算,并给出了完整代码实现和相应的实际应用例子.
6 参考
参考:
链接一
链接二
关注公众号《AI算法之道》,获取更多AI算法资讯。
![]()
注: 完整代码,关注公众号,后台回复 iou , 即可获取。