Jain‘s Faireness index如何度量TCP公平性

导语：
本文并非源自于突发奇想。好多年前第一次接触Jain’s Faireness index公式，我甚至记不下来它的形式，也不指望能弄懂它的含义。
后来发现任意学科的绝大多数问题都是可以抽象成数学问题，这些数学问题几乎都可以仅通过四则混合运算，开方，简单的微积分描述和解决，而这些知识对于一个小学高年级学生而言都是可以理解的。
最近周末偶尔会给小小灌输一些数学思想，顺便用简单的数学去梳理以前自己似懂非懂的专业领域，作此文。
但这不是唯一一篇，前面写过多篇，后面也还有。

互联网作为一个自治系统，带宽资源在所有数据流之间是共享的，互联网得以运行的关键如如何在所有这些数据流之间公平合理地分配带宽。

TCP作为一个广泛部署的端到端协议，拥塞控制是避免互联网崩溃的前提，其中最重要的是带宽资源分配的公平性(对于避免拥塞而言，公平是最重要的，而不是效率)，公平性是评价一个拥塞控制算法的重要指标。

那么如何度量一个拥塞控制算法的公平性，常用的方式即使用一个公式，即Jain’s Faireness index。

设一共有$n$条流共享带宽，$x_i$为第$i$条流的带宽分配情况(或为cwnd，或为pacing rate，随意)，

$F(x_1,...x_n)=\frac{({\Sigma }_{i=1}^n{x}_i{)}^2}{n{\Sigma }_{i=1}^n{x}_i^2}\in [\frac{1}{n},1]$

$F$数值越大，公平性越好。

$F$为什么是这种形式？为什么它能度量公平性？背后有什么直观含义？我Google了好久都没有找到答案。正好最近跟朋友讨论过这个问题，在经过一些思考后，我决定自己写一篇。

从形式上看，Jain’s Faireness index实际上就是柯西不等式的一个特殊情况。

柯西不等式如下：

${\Sigma }_{k=1}^n{a}_k^2{\Sigma }_{k=1}^n\ge ({\Sigma }_{k=1}^n{a}_k{b}_k{)}^2$【当且仅当$\frac{a_1}{b_1}=\frac{a_2}{b_2}=...\frac{a_n}{b_n}$时取等号】

令$b_1=b_2=...b_n=1$，则柯西不等式化为：

${\Sigma }_{k=1}^n{a}_k^2\times n\ge ({\Sigma }_{k=1}^n{a}_k{)}^2$

两边除以左边，可得：

$1\ge \frac{({\Sigma }_{k=1}^n{a}_k{)}^2}{n{\Sigma }_{k=1}^n{a}_k^2}$【当且仅当$a_1=a_2=...a_n$时取等号】

这就是Jain’s Faireness index，而且连取值范围都有了。

虽然数学形式很清晰，但仅从柯西不等式本身，依然无法看出$F$的直观含义，为什么$x_1=x_2=...x_n$就最公平，为什么随着$x_i$之间偏差逐渐变大，$F$会逐渐变小。

从柯西不等式分析Jain’s Faireness index是最完备且优雅的，但在此之前我想分享一些自己思考的成果。我把柯西不等式的几何意义分析放在本文最后，现在暂且忘掉它，先来直观感受Jain’s Faireness index。

如果能有个动态的过程就太好了，于是想办法构造。

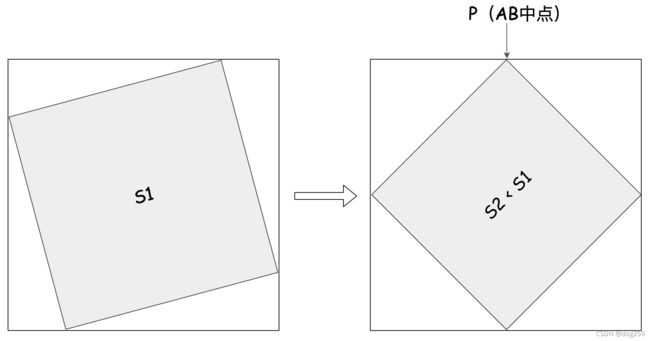
先从2条流说起，设$x_1$，$x_2$为其对应的资源，根据毕达哥拉斯定理的面积证明法，构造下面边长为1的正方形和其内接正方形：

有下列等式成立：

$x_1+x_2=1$
$x_1^2+x_2^2=h^2$

移动P点可改变$x_1$，$x_2$的大小，观察以$h$为边长的内接正方形面积S的变化。就像转万花筒一样，P点从A移动到AB中点的过程中，S逐渐变小，此后在接近B的过程中，S又逐渐增大。

这个动态过程正好可以如下度量公平性：

• 当P点位于A点或者B点附近时最不公平，此时S最大。
• P点逐渐从A或B接近中点的过程中，S单调递减。
  接下来将这个过程向Jain’s Faireness index靠拢。

不妨将S的倒数作为公平性度量。求出S的范围：

$\frac{1}{S}=\frac{1}{x_1^2+x_2^2}=\frac{1}{h^2}$
$S_{max}=1$
$S_{min}=(\frac{\sqrt{2}}{2}{)}^2=\frac{1}{2}$

因此，Jain’s Faireness index的物理意义其实就是S的大小：
$1\le \frac{(x_1+x_2{)}^2}{x_1^2+x_2^2}\le 2$

两边除以2，可得：

$F(x_1,x_2)=\frac{(x_1+x_2{)}^2}{2(x_1^2+x_2^2)}\in [\frac{1}{2},1]$

接下来，3条流，4条流，…n条流的情况，如何像以上这样确定Jain’s Faireness index的实际意义？毕达哥拉斯定理还能挂靠吗？很难了…

毕达哥拉斯定理的面积证明法是一种拼凑法，属于奇技淫巧，但凡奇技淫巧都无法推而广之。虽难推广，但有意思，下面再来一例拼凑。

设$x_1\ge x_2$，对因式分解和勾股数敏感的人一眼就能认出一组勾股数：$\frac{x_1+x_2}{2}$，$\frac{x_1-x_2}{2}$，$\sqrt{\frac{x_1^2+x_2^2}{2}}$，如果认不出来，通过简单的平面几何构造，也能看出究竟，如下图：

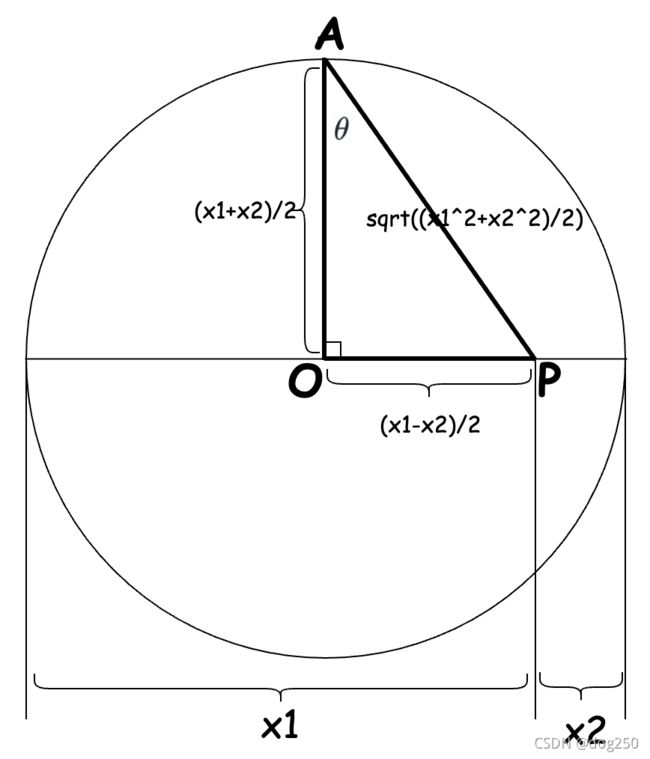
Jain’s Faireness index事实上就是${\cos }^2\theta$。

从上图中可以直观感受到，随着$x_1$和$x_2$逐渐接近，即$P$点向圆心$O$接近，$\theta$会逐渐变小，从而$\cos \theta$逐渐变大，Jain’s Faireness index趋向于公平。

若要度量n条流的带宽分配公平性，并展示其公平性的实际意义，我采用解析几何的方法，寻找
Jain’s Faireness index的几何意义。

依然设总带宽资源为单位1，先从2条流开始。构造下面的二维笛卡儿坐标系：

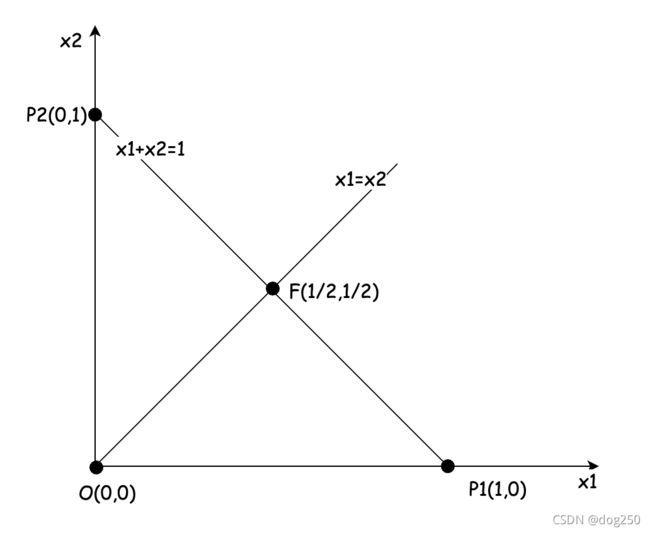
该坐标系中的两个重要方程：

• 公平直线方程：$x_1=x_2$
• 资源直线方程：$x_1+x_2=1$
  根据点到直线上的点，垂线段最短，可得：
• 原点$O$到资源直线距离最近的点为上述两个直线的交点$F(\frac{1}{2},\frac{1}{2})$。
• 原点$O$到资源直线距离最远的点为$P_1(1,0)$和$P_2(0,1)$。
• 在资源直线上从$F$移向$P_1$或$P_2$的过程中，到原点$O$的距离逐渐增大。
  

可得下面的不等式：

$\frac{\sqrt{2}}{2}\le \sqrt{x_1^2+x_2^2}\le 1$

其中，$\frac{\sqrt{2}}{2}$由于上述公平直线方程和资源直线方程联立求得。因此：

$1\le 2(x_1^2+x_2^2)\le 2$

由于$x_1+x_2=1$，取倒数，将取值限制在区间$[\frac{1}{2},1]$:

$\frac{1}{2}\le \frac{(x_1+x_2{)}^2}{2(x_1^2+x_2^2)}\le 1$

看，这就是2条流时的Jain’s Faireness index。

很容易扩展到3条流。构造三维坐标系：

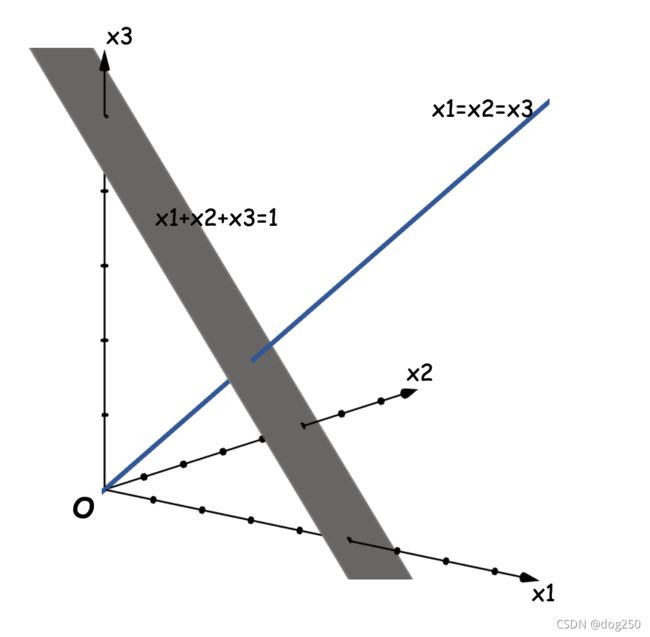
该坐标系中的两个重要方程：

• 公平直线方程：$x_1=x_2=x_3$，注意，任何维度下，均收敛到公平直线。
• 资源平面方程：$x_1+x_2+x_3=1$
  根据点到平面上的点，垂线段最短，可得：
• 原点$O$到资源平面距离最近的点为上述两个直线的交点$F(\frac{1}{3},\frac{1}{3},\frac{1}{3})$。
• 原点$O$到资源直线距离最远的点为$P_1(0,0,1)$，$P_2(0,1,0)$和$P_3(1,0,0)$。
• 在资源平面(注意不再是直线)上从$F$移向$P_1$，$P_2$或$P_3$的过程中，到原点$O$的距离逐渐增大。
  可得下面的不等式：

$\frac{\sqrt{3}}{3}\le \sqrt{x_1^2+x_2^2+x_3^2}\le 1$

其中，$\frac{\sqrt{3}}{3}$由于上述公平直线方程和资源直线方程联立求得。因此：

$1\le 3(x_1^2+x_2^2+x_3^2)\le 3$

其中，$\frac{\sqrt{3}}{3}$由于上述公平直线方程和资源平面方程联立求得。

由于$x_1+x_2+x_3=1$，取倒数，将取值限制在区间$[\frac{1}{3},1]$:

$\frac{1}{3}\le \frac{(x_1+x_2+x_3{)}^2}{3(x_1^2+x_2^2+x_3^2)}\le 1$

看，这就是3条流时的Jain’s Faireness index。

很容易扩展到4条流。构造四维坐标系：
… 不过画不出来了…

当存在$n$条流时，资源分配体现为$n$维坐标系下资源超平面$x_1+x_2+...x_n=1$上的点，公平性的度量就是原点$O$到资源超平面上点距离的倒数。如果该距离最短，则资源分配绝对公平，该点一定是资源超平面和公平直线的交点$P_{fair}(\frac{1}{n},\frac{1}{n},\frac{1}{n},...\frac{1}{n})$。资源分配点在资源超平面偏离$P_{fair}$越远，原点$O$到该点的距离就越大，其倒数就越小，体现为越不公平。是不是很形象呢？

OK，在结束本文之前，我兑现最开始的承诺，用柯西不等式来正式描述Jain’s Faireness index。先从柯西不等式的几何意义开始。

定义二维向量$a=[a_1,a_2]$，$b=[b_1,b_2]$
设向量$c$如下：

$c=[c_1,c_2]=a-b$

根据余弦定理：

$|c{|}^2=|a{|}^2+|b{|}^2+2|a||b|\cos \theta$

$c$表达式恒等式展开：

$c\cdot c=(a-b)\cdot (a-b)=a\cdot a-2a\cdot b+b\cdot b$

根据点乘定义：

$c\cdot c=c_1{c}_1+c_2{c}_2=c_1^2+c_2^2=|c{|}^2$

所以：

$|c{|}^2=|a{|}^2+|b{|}^2+2a\cdot b$

结合余弦定理的形式，可得：

$a\cdot b=|a||b|\cos \theta \le |a||b|$

根据点乘定义以及距离公式：

$a\cdot b=a_1{b}_1+a_2{b}_2\le \sqrt{a_1^2+a_2^2}\sqrt{b_1^2+b_2^2}$

取平方得：

$(a_1{b}_1+a_2{b}_2{)}^2\le (a_1^2+a_2^2)(b_1^2+b_2^2)$

这就是柯西不等式在二维空间的情况。现在推广到三维空间很容易。三维空间的推导和二维空间完全一致，只是$a$与$b$形成的平面可能是斜的，夹角$\theta$依然是一个夹角。

对于$n(n\ge 4)$维空间，虽然无法想象，但对于数学推导依然不变，比如：

$c\cdot c=c_1^2+c_2^2+...c_n^2=|c{|}^2$

高维空间虽然不可想象，$a$与$b$两个向量永远组成一个二维平面，在二维平面上的夹角$\theta$永远和二维空间的情形完全一致。

将$n$维空间的柯西不等式变换一下形式：

$\frac{(a_1{b}_1+a_2{b}_2+...a_n{b}_n{)}^2}{(a_1^2+a_2^2+...a_n^2)(b_1^2+b_2^2+...b_n^2)}={\cos }^2\theta \le 1$

不等式左边正好可以表示${\cos }^2\theta$，柯西不等式的几何意义在于：

• 在$n(n\in N)$维空间，不等式左边可以度量两个$n$维向量夹角$\theta$的余弦值。
  显然，$\theta$越小，不等式左值越大，当$\theta =0^o$时，不等式左值等于1。OK，已经趋于清晰。

现在假设两个$n$维向量其中的$b$已经确定：

$b=[1,1,...1]$

代入柯西不等式：

$\frac{(a_1+a_2+...a_n{)}^2}{n(a_1^2+a_2^2+...a_n^2)}={\cos }^2\theta \le 1$

以上就是完整的Jain’s Faireness index！

$n$条流共享带宽，构造$n$维空间，向量$b$记为$OB$，点$B$坐标为$(1,1,...1)$，空间中的点$P(a_1,a_2,...a_n)$可以代表一个资源分配点，它的几何意义就是：

• 对于总量固定的资源，所有满足条件的$P$点均在一个超平面$x_1+x_2+...+x_n=1$上。
• 公平性度量可以表示为原点$O$到资源分配点$P$的向量$OP$与向量$OB$之间夹角$\theta$的余弦值的平方。
  显然，$\theta$越大，说明资源分配越不公平，$\theta$越小，说明资源分配越公平。

参考

• 1984年Jain’s paper：https://arxiv.org/pdf/cs/9809099.pdf

浙江温州皮鞋湿，下雨进水不会胖。