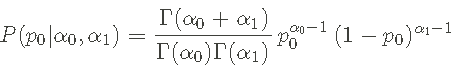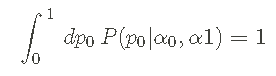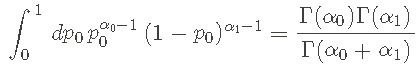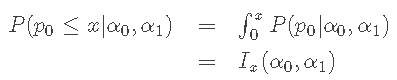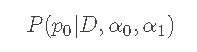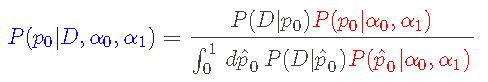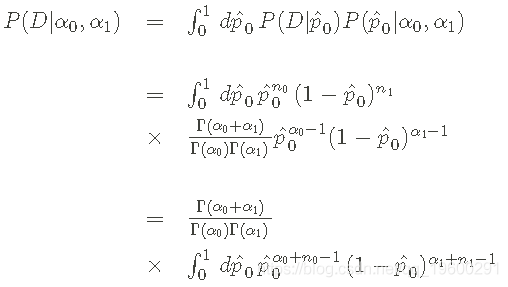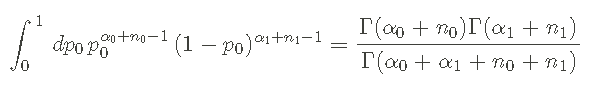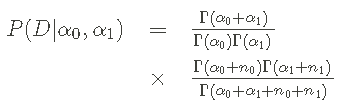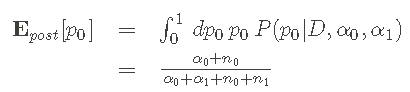原文链接:http://tecdat.cn/?p=24084
在这篇文章中,我将扩展从数据推断概率的示例,考虑 0 和 1之间的所有(连续)值,而不是考虑一组离散的候选概率。这意味着我们的先验(和后验)现在是一个 probability density function (pdf) 而不是 probability mass function (pmf)。
我考虑了从数据序列推断 p0,即零的概率:
_我_使用 p0的不同先验来_解决相同的问题,该_先验允许 0 和 1 之间的连续值而不是一组离散的候选值。
概率
我们推理问题的起点是 _似然_ ——观察到的数据序列的概率,写成就像我知道 p0 的值一样:
为了清楚起见,我们可以插入 p0=0.6,并找到给定未知概率值的指定数据序列的概率:
可能性的更一般形式,不是特定于所考虑的数据序列,是
其中 n0 是零的数量,n1 是考虑的任何数据序列 D 中的 1 的数量。
先验 - Beta 分布
我们使用贝塔分布来表示我们的先验假设/信息。其数学形式是
其中 α0 和 α1 是我们必须设置的超参数,反映我们关于 p0 值的假设/信息。但是,只需将p0 视为我们想要推断的参数——忽略参数是概率。
请注意 后验 pdf 也将是 Beta Distribution,因此值得努力适应 pdf。
先验均值—— 大多数人想要一个数字或点估计来表示推理结果或先验中包含的信息。然而,在贝叶斯推理方法中,先验和后验都是 pdf 或 pmf。获得点估计的一种方法是取 相关参数相对于先验或后验的 _平均值_。例如,对于 Beta 先验我们得到:
pdf 被归一化—— 这意味着如果我们将 p0 从 0 积分到 1,我们会得到一个:
因为以下关系:
就我们而言,最重要的信息是 b 在 0 到 1 区间上进行归一化,这对于像 p0 这样的概率是必要的。
先验假设和信息可以通过设置超参数来反映--超参数α0α0和α1α1影响pdf的形状,使先验信息的编码更加灵活。
例如,使用α0=1, α1=1 不能反映p0 的优选值。这个pdf看起来像
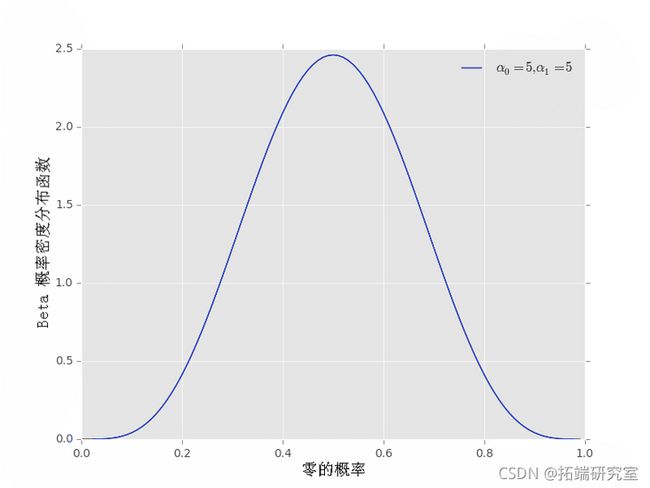
另一个先验可以指定 α0=5, α1=5,它更接近 p0=1/2 附近的值
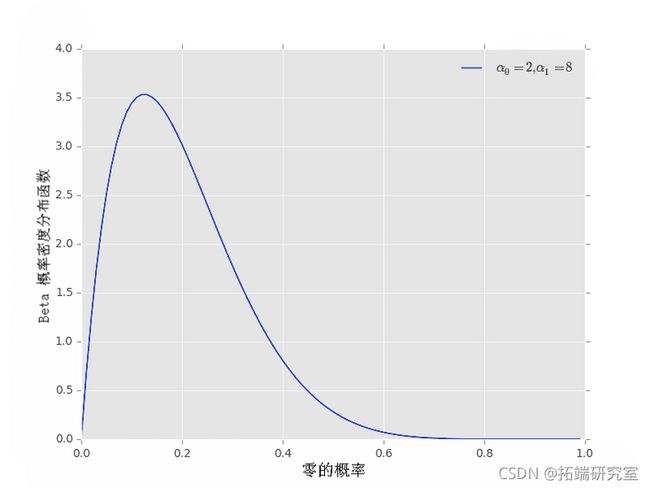
最后,我们可以用α0≠α1得到非对称的先验,可以看到α0=2,α1=8。
关于设置超参数需要记住的一些事情:
- 如果 α0=α1,先验将是对称的,先验平均值等于 Eprior[p0]=1/2。
- 如果 α0≠α1,则先验将是不对称的,先验平均值不同于 1/21/2。
- 先验的强度与α0+α1的总和有关。将α总和与数据中的n0+n1进行比较,将α的视为假数。这些和的相对大小控制着先验和似然对后验形状的影响。这在下面的Python例子中会变得很清楚。
累积分布函数 (cdf) beta累积分布函数 (cdf)让我们计算 p0 小于或等于值 x 的概率。具体来说,cdf定义为:
该积分也被称为不完全Beta ing积分,并表示为Ix(α0,α1)。
如果我们想知道p0在数值xl和xh之间的概率,我们可以用cdf来计算。
不完全 Beta 积分或 cdf 及其逆积分允许从先验或后验计算置信区间。使用这些工具,可以说p0 的值有 95% 的概率在某个范围内——同样,我们将使用 Python 代码在下面绘制它。
贝塔分布是这个问题的共轭先验--这意味着后验将具有与先验相同的数学形式(它也是一个贝塔分布),并更新了超参数。这种数学上的 "共鸣 "真的很好,让我们不用MCMC就能做完整的贝叶斯推断。
现在我们谈谈贝叶斯定理和这个问题的后验pdf。
贝叶斯定理和后验
我们的最终目标是后验概率密度函数,结合似然和先验,在考虑数据后对我们对p0的知识做一个更新的反映。后验pdf的形式是(在这种情况下)。
换句话说,这是 _给定数据_序列 D _和先验假设的_ p0 _的概率密度__,由具有超参数_ (α0,α1)_的 Beta pdf 反映_。
在这种情况下,贝叶斯定理采用以下形式:
其中后验 P(p0|D,α0,α1) 为蓝色,似然 P(D|p0)为黑色,先验 P(p0| α0,α1)是红色的。请注意,归一化 _边际似然_ (上述等式中的分母)现在是一个积分。
尝试将贝叶斯定理视为关于 p0 从 假设 (α0,α1) 更新到 假设 + 数据 (D,α0,α1) 的信息:
试着把贝叶斯定理看作是关于p0的信息被从假设(α0,α1)更新为假设+数据(D,α0,α1)。
为了得到后验pdf,我们必须在贝叶斯定理的分母上做积分。在这种情况下,利用贝塔分布的特性,就可以进行计算。该积分如下。
最后一行的积分定义了一个贝塔函数,在关于先验的一节中讨论过,并且有一个已知的结果。
这意味着分母,也叫边际似然,等于。
同样,我们得到这个结果是因为Beta分布是我们所考虑的伯努利过程可能性的共轭先验。请注意,来自先验的超参数已经被计数数据所更新。
这与人们预期的完全一样,不需要做所有的数学计算。在任何情况下,在用Python实现这一点之前,有几个注意事项。
- 后验pdf在0到1的区间内被归一化,就像我们推断p0这样的概率时需要的那样。
- 后验平均数,是对我们的推断给出一个点估计的方法是
- 后验的cdf和先验的一样,因为我们仍然有一个Beta分布--只不过,现在的参数是用数据更新的。在任何情况下,我们都可以用不完整的Beta积分和它的逆向找到置信区间,如上所述。
Python 中的推理代码
首先,我们导入一些包,使用这些包来计算和绘制先验、似然和后验。此外,使用 matplotlib,在本例中为 ggplot,创建漂亮的图。
概率
def _int(sef, daa):
""二进制数据的概率。""
elfus = {s:0 for s in \['0', '1'\]}
def proes_data(sef, ata):
""处理数据。""
for s in \['0', '1'\]:
unts\[s\] =cont(s)
""处理概率。""
n0 = couts\['0'\]
n1 = couts\['1'\]
if p0 != 0 and p0 != 1:
# 典型情况
lgpdaa = n0*log(p0) + \
n1*log(1.-p0)
rdta = exp(lgpata)
elif p0 == 0 and n0 != 0:
# 如果n0不是0,p0就不可能是0
lpr_dta = -np.inf
p_dta = exp(lgrata)
elif p0 == 0 and n0 == 0:
# 数据与p0=0一致
lgpr_at = n1*np.log(1.-p0)
p\_ata =.exp(lo\_dta)
elif p0 == 1 and n1 != 0:
# 如果n1不是0,p0就不可能是1
lpdta = -inf
praa = exp(lor_ta)
elif p0 == 1 and n1 == 0:
# 数据与p0=1一致
log_dta = n0*log(p0)
def prob(sef, p0):
""获取数据的概率。"""
prdat,_ = .\_procs\_proabiti(p0)
def logprob(sef, p0):
""获取数据的概率对数。"""
_, lgpr\_a = sel\_presplies(p0)先验分布
我们的先验类基本上是一个围绕 scipy的包,有一个绘图方法。注意 plot() 方法得到了 Beta 分布的平均值,并使用 interval() 方法得到了一个概率为 95% 的区域--这是使用不完整的 Beta 积分和上面讨论的它的逆值完成的。
def \_int\_(sef, alpa0=1, alph1=1):
""二进制数据的β先验。""
elfa0 = alha0
sl.1 = alha1
slf.0r = ba(self.0, sef.a1)
def intrval(slf, pb):
""包含`prob'的pdf区域的端点。
例如:interval(0.95)
"""
return sef.pvitervl(rob)
def mean(self):
"""返回先验平均数。"""
def pdf(self, p0):
"""p0处的概率密度。"""
return self.p.pdf(p0)
def plot(self):
""显示平均值和95%置信区间的图。""
fig, ax = tsuplots(1, 1)
x = np.rae(0., 1., 0.01)
# 获得先验平均数 p0
mean = mean()
# 获得包含95%概率的低/高点
low\_p0, high\_p0 = l.nterval(.95)
xo =nang(\_0, hih\_p0, 0.01)
# 绘制pdf
ax.plot(x, self.pdf(x), 'r-')
# 填充95%的区域
between(x\_prob 0, sel.pdf(x\_pob)
# 平均值
ax.stem(\[mean\], \[sf.df(mea)让我们使用新代码绘制一些具有一序列参数的 Beta pdf。
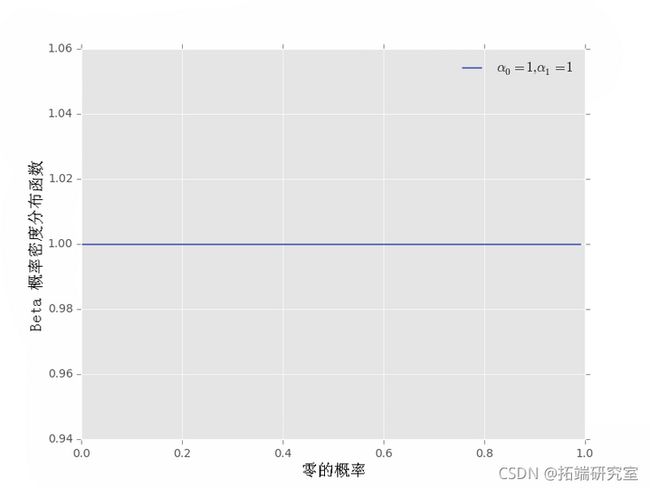
统一先验
带点的垂直线显示 pdf 均值的位置。阴影区域表示对于给定的 α0 和 α1 值,概率为 95% 的(对称)区域。如果您想要平均值和置信区间的实际值,也可以获取这些值:
print("先验均值: {}".format(pri.mean()))上面的其他先前示例也有效:
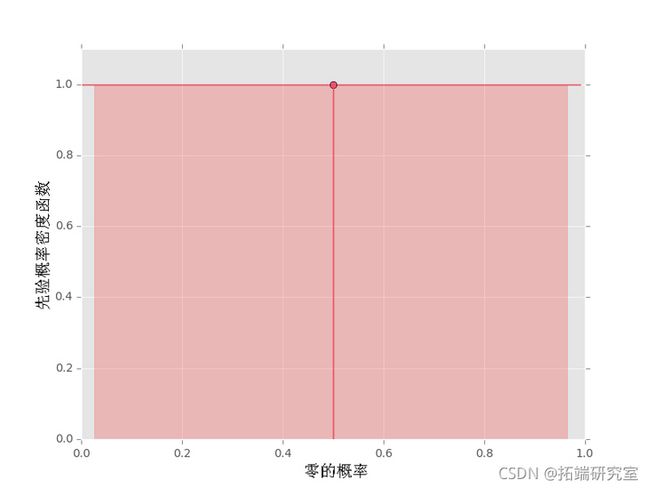
prior(5, 5)
plot()和
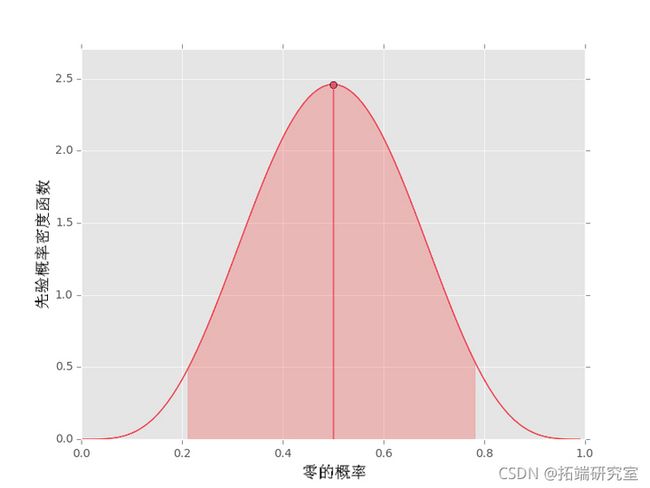
por(2, 8)
iplot()了解超参数所反映的先前假设的均值和不确定性很有用。
后验
最后,我们为后验构建类。正如您所料,我将数据和先验作为参数,并从这些元素中提取后验所需的参数。
def \_\_int\_(sf datprior):
""后验。
data: 一个数据样本的列表
先验:β先验类的一个实例
"""
elflilihod = liliod(dta)
sefprir = rio
self.\_css\_steror()
def \_pces\_posteror(slf):
""使用传递的数据和先验来处理后验。""
# 从似然和先验中提取n0, n1, a0, a1
seln = slfliklihod.counts\['0'\]
sel.n1 = elf.lkelihodcnts\['1'\]
lfa0 = sf.prir.0
self.a = sef.priora
el0rv= beta(selfa0 + sfn0,
sef.a1 + slf.1)
def interalself, prob):
""含\`prob\`的pdf区域的端点。
例如:interval(0.95)
"""
def mean(sef):
"""返回后验平均数。"""
def pdf(sef, p0):
"""p0处的概率密度。"""
def plot(slf):
""显示先验、似然和后验的图。""
## 先验
# 得到先验平均数 p0
pri_mean =eorman()
#得到包含95%概率的低/高分值
plo_p0,= interval(0.95)
prob = arange(low\_p0, i\_hgh_0, 0.01)
# 绘制pdf
plot(prior.pdf(x)
# 填充95%的区域
x.ll\_between(pri\_p )
# 平均值
astm(\[pri_mean\])
## 似然
# 绘制似然图
li = \[sel.likliood.pro\]
# ##后验
#获得后验平均数p0
ostmen = mean()
#得到包含95%概率的低/高点
ow\_p0, \_high_p0 = interval(0.95)
prob = np.rngest\_low\_p0po_highp0 0.01)
# 绘制pdf
plot(x, slf.pd(x)
# 填充95%的区域
fil\_etween(pos\_xob, 0,self.df(pt_pr )
# 平均值
ax2\].t_mean\])基本代码就是这样,让我们做一些例子。
例子
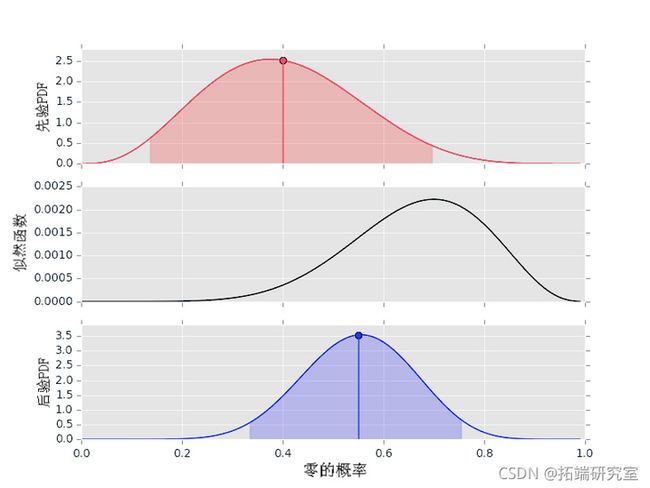
让我们从数据和统一先验的示例开始。
# 数据
data1 = \[0,0,0,0,1,1,0,0,0,1\]
# 先验
pro1 = prir(1, 1)
# 后验
ot1 = psteior(daa1, ior1)
plot()这里需要注意的事项:
- 先验是统一的。这意味着概率和后验具有相同的形状。
- 95%的置信区间同时显示在先验和后验中。
接下来,让我们考虑具有不统一先验的相同数据。数据集长度为 10,因此 n0+n1=10。让我们用 α0+α1=10 ,设置先验,但先验在与似然不同的位置达到峰值(也许有专家说这应该是先验设置):
# 先验
prir(4, 6)
# 后验
ps2 = postior(da1, pio2)
plot()显然数据和专家在这一点上存在分歧。然而,因为先验的权重设置为 10 并且数据序列的长度为 10,所以后验峰值位于先验峰值和似然峰值的中间。尝试使用这种效果来更好地理解先验超参数、数据集长度和结果后验之间的相互作用。
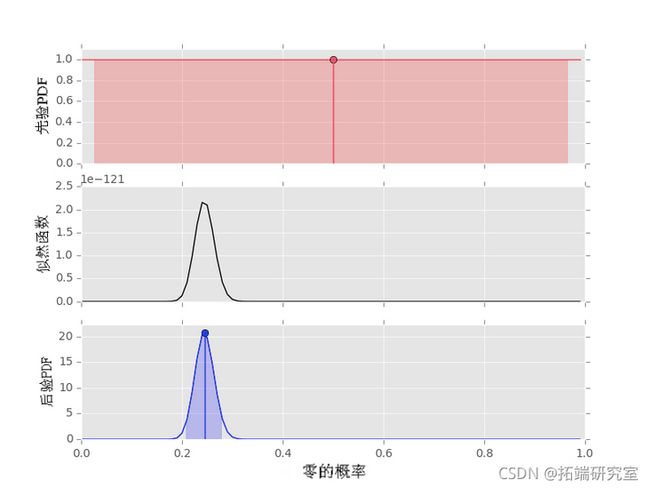
作为最后一个例子,我们考虑最后一个例子的两个变体, 首先我们使用统一先验:
# 设定概率为0
p0 = 0.2
#设置rng种子为2
n.rand.sed(2)
# 产生数据
dta2 =rando.i(\[0,1\], 500, p=\[p0, 1.-p0\])
# 先验
prior(1,1)
# 后验
poteir(daa2, pio3)请注意,概率和后验峰值在同一个地方,正如我们所期望的那样。但是,由于数据集较长(500 个值),峰值要强得多。
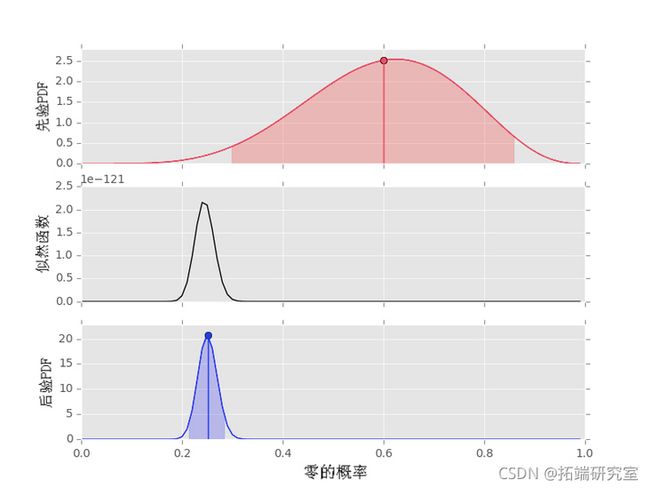
最后,我们在同一数据集上使用“错误先验”。在这种情况下,我们将保持先验强度为 10,即 α0+α1=10:
# 先验
prior(6,4)
# 后验
poseor(data, pior4)请注意,尽管先验在错误的位置达到峰值,但可能性和后验非常相似。这个例子表明,如果先验没有设置得太强,合理数量的数据应该产生不错的推理。一般来说,最好让 n0+n1>α0+α1 并考虑先验和后验的形状。
最受欢迎的见解
4.R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归