人工智能之数学基础篇—高等数学基础
人工智能之数学基础篇—高等数学基础
- 1 函数
-
- 1.1 函数的定义
- 1.2 几种特殊函数的定义
- 1.3 函数的几种特性
- 2 极限
-
- 2.1 数列
- 2.2 收敛数列的性质
在这篇文章,我将简单的总结一下函数、极限、无穷大和无穷小、连续性与导数、偏导数、方向导数、梯度等高等数学基本概念,这些概念是理解人工智能算法的基础数学知识。其中梯度下降算法是机器学习领域的重要算法,是应用最广泛的优化算法之一。在本篇文章中,我将结合综合实例来介绍梯度下降算法,并通过Python语言编程实现。
1 函数
我们经常会遇到彼此之间有依赖关系的变量,如圆的面积 s s s 与它的半径 r r r 之间存在 s = π r 2 s=\pi r^{2} s=πr2,自由落体运动中,若开始下落的时刻为 t = 0 t=0 t=0,则下落的距离 h h h 与下落的时间 t t t 之间存在 h = 1 2 g t 2 h=\frac{1}{2}gt^{2} h=21gt2 关系。我们称这种依赖关系为函数关系。
1.1 函数的定义
定义1.1 设数集 D ⊂ R D\subset R D⊂R,则映射 f : D → R f:D\rightarrow R f:D→R 为定义在 D D D 上的函数,通常简记为 y = f ( x ) , x ϵ D y=f(x),x\epsilon D y=f(x),xϵD。其中 x x x 称为自变量, y y y 称为因变量, D D D 称为定义域,记作 D f D_{f} Df,即 D f = D D_{f}=D Df=D。
按此定义,对每个 x ϵ D x\epsilon D xϵD,按对应法则 f f f,总有唯一确定的值 y y y 与之对应,这个值称为函数 f f f 在 x x x 处的函数值,记作 f ( x ) f(x) f(x),即 y = f ( x ) y=f(x) y=f(x)。因变量 y y y 与自变量 x x x 之间的这种依赖关系通常称为函数关系。函数值 f ( x ) f(x) f(x) 的全体所构成的集合称为函数的值域,记作 R f R_{f} Rf 或 f ( D ) f(D) f(D),即 R f = f ( D ) = { y ∣ y = f ( x ) , x ϵ D } R_{f}=f(D)=\left \{ y\mid y=f(x),x\epsilon D \right \} Rf=f(D)={ y∣y=f(x),xϵD}。
函数的定义域通常由函数的实际意义所决定,如圆的面积 s = π r 2 s=\pi r^{2} s=πr2,其中 r r r 为自变量,而实际上圆的半径不可能为负数,因此函数定义域为 D = [ 0 , ∞ ) D=\left [ 0,\infty \right ) D=[0,∞)。
函数在 x 0 x_{0} x0 处取得的函数值 y 0 = y ∣ x = x 0 = f ( x 0 ) y_{0}= y \mid _{x=x_{0}} = f\left ( x_{0} \right ) y0=y∣x=x0=f(x0)
1.2 几种特殊函数的定义
1.分段函数
定义1.2 对于自变量 x x x 的不同的取值范围,有着不同的对应法则,这样的函数称为分段函数。
【例1.1】分段函数
f ( x ) = { x if x ≥ 0 x if x < 0 f\left ( x \right ) = \begin{cases} \sqrt{x} & \text{ if } x \geq 0 \\ x & \text{ if } x < 0 \end{cases} f(x)={ xx if x≥0 if x<0
2.反函数
定义1.3 设函数 f : D → f ( D ) f:D\rightarrow f\left ( D \right ) f:D→f(D) 是单射,则存在逆映射 f − 1 : f ( D ) → D f^{-1}:f\left ( D \right )\rightarrow D f−1:f(D)→D,称此映射 f − 1 f^{-1} f−1 为函数 f f f 的反函数。
按此定义,对每个 y ϵ f ( D ) y \epsilon f\left ( D \right ) yϵf(D),有唯一的 x ϵ D x\epsilon D xϵD,使得 f ( x ) = y f\left ( x \right ) = y f(x)=y,于是有 f − 1 ( y ) = x f^{-1}\left ( y \right ) = x f−1(y)=x。也就是说反函数 f − 1 f^{-1} f−1 的对应法则完全由函数 f f f 的对应法则所确定。
【例1.2】求 h = 1 2 g t 2 h = \frac{1}{2}g t^{2} h=21gt2 的反函数。
解:
h = f ( t ) , t = f − 1 ( h ) → t = 2 h g h=f\left ( t \right ), t=f^{-1}\left ( h \right )\rightarrow t=\sqrt{\frac{2h}{g}} h=f(t),t=f−1(h)→t=g2h
即原函数的反函数为 t = 2 h g t=\sqrt{\frac{2h}{g}} t=g2h。
3.显函数与隐函数
定义1.4 一个函数如果能用形如 y = f ( x ) y=f(x) y=f(x) 的解析式表示,其中 x x x、 y y y 分别是函数的自变量与因变量,则此函数称为显函数。例如, y = x 2 + 1 y = x^{2} + 1 y=x2+1 即为显函数。
定义1.5 如果由方程 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0 可确定 y y y 是 x x x 的函数,即 x x x、 y y y 在某个范围内存在函数 y = g ( x ) y=g(x) y=g(x),使 F [ x , g ( x ) ] = 0 F\left [ x,g\left ( x \right ) \right ] = 0 F[x,g(x)]=0,则这个函数是隐函数。例如, x 2 + 1 − y 2 = 0 x^{2} + 1 - y^{2} = 0 x2+1−y2=0 就是隐函数。
1.3 函数的几种特性
1.函数的奇偶性
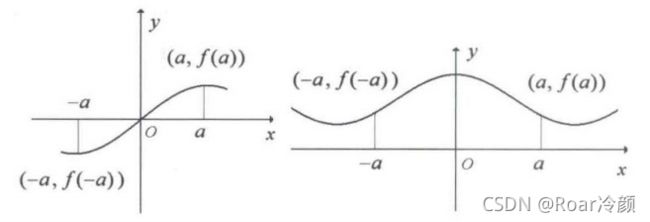
设函数 y = f ( x ) y=f(x) y=f(x) 的定义域 D D D 关于原点对称。对于区间 D D D 上任意点 x x x,若 f ( − x ) = − f ( x ) f(-x)=-f(x) f(−x)=−f(x) 恒成立,则 f ( x ) f(x) f(x) 为奇函数。若 f ( − x ) = f ( x ) f(-x)=f(x) f(−x)=f(x) 恒成立,则 f ( x ) f(x) f(x) 为偶函数。
从几何意义上说,一个奇函数,其图像在绕原点180°旋转后不会改变。一个偶函数关于 y y y 轴对称,其图像在对 y y y 轴映射后不会改变,如图1所示。
2.函数的单调性
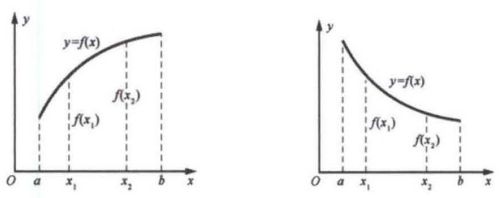
设函数 f ( x ) f(x) f(x) 的定义域为 D D D,区间 I ⊂ D I \subset D I⊂D。假设区间 I I I 上有任意两点 x 1 x_{1} x1 及 x 2 x_{2} x2:当 x 1 < x 2 x_{1} < x_{2} x1<x2 时,恒有 f ( x 1 ) < f ( x 2 ) f(x_{1})
3.函数的周期性
设函数 f ( x ) f(x) f(x) 的定义域为 D D D,如果存在一个正数 T T T,使任意点 x ϵ D x \epsilon D xϵD 有 ( x ± T ) ϵ D (x±T) \epsilon D (x±T)ϵD,且 f ( x ± T ) = f ( x ) f(x±T)=f(x) f(x±T)=f(x)恒成立,则称 f ( x ) f(x) f(x) 为周期函数, T T T 称为 f ( x ) f(x) f(x) 的周期,通常说周期函数的周期是指最小正周期。
如图3所示,函数 s i n x sinx sinx、 c o s x cosx cosx 都是以 2 π 2\pi 2π 为周期的周期函数,函数 t a n x tanx tanx 是以 π \pi π 为周期的周期函数。
2 极限
极限概念是在探求某些实际问题的精确解答过程中产生的。例如,求解曲边梯形的面积就是采用划分无穷个小梯形面积,然后求和得出曲边梯形的近似面积的方法,即极限思想在积分学的应用。另外以泰勒多项式近似表达复杂函数,也是极限思想的应用。极限方法是高等数学中的一种基本方法。
2.1 数列
定义1.6 如果按照某一法则,对每一个 n ϵ N + n \epsilon N_{+} nϵN+,对应着一个确定的实数 u n u_{n} un,按照下标 n n n 从小到大排列得到的序列 u 1 , u 2 , . . . , u n u_{1}, u_{2},...,u_{n} u1,u2,...,un 就叫作数列,简记为数列 { u n } \left \{ u_{n} \right \} { un},其中 u n u_{n} un 叫作通项。
对于数列 { u n } \left \{ u_{n} \right \} { un} 而言,如果 n n n 无限增大,其通项无限接近常数 A A A,则称该数列以 A A A 为极限或称数列收敛于 A A A,记为 lim n → ∞ u n = A \lim_{n\rightarrow \infty } u_{n}=A limn→∞un=A ,否则称数列为发散。
2.2 收敛数列的性质
定理1.1 (极限的唯一性)如果数列 { u n } \left \{ u_{n} \right \} { un} 收敛,那么它的极限唯一。
定理1.2 (收敛数列的有界性)如果数列 { u n } \left \{ u_{n} \right \} { un} 收敛,那么数列 { u n } \left \{ u_{n} \right \} { un} 一定有界。
注意:数列有界是数列收敛的必要条件,但不是充分条件。
定理1.3 (收敛数列的保号性)如果 lim n → ∞ u n = a \lim_{n\rightarrow \infty } u_{n}= a limn→∞un=a,且 a > 0 a>0 a>0(或 a < 0 a < 0 a<0),那么存在正整数 N N N,当 n > N n>N n>N时,则 u n > 0 u_{n} > 0 un>0 (或 u n < 0 u_{n} < 0 un<0)。
定理1.4 (收敛数列与其子序列的关系)如果数列 { u n } \left \{ u_{n} \right \} { un} 收敛于 a a a,那么它的任意子序列也收敛,且极限为 a a a。