原文链接: http://tecdat.cn/?p=24092
前言
在量化金融中,我学习了各种时间序列分析技术以及如何使用它们。
通过发展我们的时间序列分析 (TSA) 方法组合,我们能够更好地了解已经发生的事情,_并对_未来做出更好、更有利的预测。示例应用包括预测未来资产收益、未来相关性/协方差和未来波动性。
在我们开始之前,让我们导入我们的 Python 库。
import pandas as pd
import numpy as np让我们使用pandas包通过 API 获取一些示例数据。
# 原始调整后的收盘价
daa = pdDatrme({sx(sm)for sm i syos})
# 对数收益率
ls = log(dta/dat.sit(1)).dropa()基础知识
什么是时间序列?
时间序列是按时间顺序索引的一系列数据点。—— Wikipedia
平稳性
为什么我们关心平稳性?
- 平稳时间序列 (TS) 很容易预测,因为我们可以假设未来的统计属性与当前的统计属性相同或成比例。
- 我们在 TSA 中使用的大多数模型都假设协方差平稳。这意味着这些模型预测的描述性统计数据(例如均值、方差和相关性)仅在 TS 平稳时才可靠,否则无效。
“例如,如果序列随着时间的推移不断增加,样本均值和方差会随着样本规模的增加而增长,并且他们总是会低估未来时期的均值和方差。如果一个序列的均值和方差是没有明确定义,那么它与其他变量的相关性也不是。”
话虽如此,我们在金融中遇到的大多数 TS 都不是平稳的。因此,TSA 的很大一部分涉及识别我们想要预测的序列是否是平稳的,如果不是,我们必须找到方法将其转换为平稳的。(稍后会详细介绍)
自相关
本质上,当我们对时间序列建模时,我们将序列分解为三个部分:趋势、季节性/周期性和随机。随机分量称为残差或误差。它只是我们的预测值和观察值之间的差异。序列相关是指我们的 TS 模型的残差(误差)彼此相关。
为什么我们关心序列相关性?
我们关心序列相关性,因为它对我们模型预测的有效性至关重要,并且与平稳性有着内在的联系。回想一下,根据定义,_平稳_TS的残差(误差)是连续_不相关_的!如果我们在我们的模型中没有考虑到这一点,我们系数的标准误差就会被低估,从而夸大了我们的 T 统计量。结果是太多的 1 类错误,即使原假设为真,我们也会拒绝原假设!通俗地说,忽略自相关意味着我们的模型预测将是胡说八道,我们可能会得出关于模型中自变量影响的错误结论。
白噪声和随机游走
白噪声是我们需要了解的第一个时间序列模型(TSM)。根据定义,作为白噪声过程的时间序列具有连续不相关的误差,这些误差的预期平均值等于零。对连续不相关的误差的另一种描述是,独立和相同分布(i.i.d.)。这一点很重要,因为如果我们的TSM是合适的,并且成功地捕捉了基本过程,我们模型的残差将是i.i.d.,类似于白噪声过程。因此,TSA的一部分实际上是试图将一个模型适合于时间序列,从而使残差序列与白噪声无法区分。
让我们模拟一个白噪声过程并查看它。下面我介绍一个方便的函数,用于绘制时间序列和直观地分析序列相关性。
我们可以轻松地对白噪声过程进行建模并输出 TS 图检查。
np.random.seed(1)
# 绘制离散白噪声的曲线
ads = radooral(size=1000)
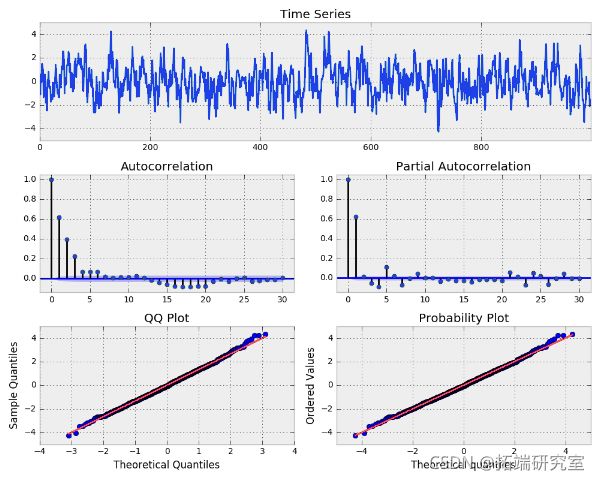
plot(ads, lags=30)高斯白噪声
我们可以看到该过程似乎是随机的并且以零为中心。自相关 (ACF) 和偏自相关 (PACF) 图也表明没有显着的序列相关。请记住,我们应该在自相关图中看到大约 5% 的显着性,这是由于从正态分布采样的纯偶然性。下面我们可以看到 QQ 和概率图,它们将我们的数据分布与另一个理论分布进行了比较。在这种情况下,该理论分布是标准正态分布。显然,我们的数据是随机分布的,并且应该遵循高斯(正常)白噪声。
p("nmean: {:.3f}\\{:.3f}\\stde: {:.3f}"
.format(ademean(), nerva(), der.td()))随机游走的意义在于它是非平稳的,因为观测值之间的协方差是时间相关的。如果我们建模的 TS 是随机游走,则它是不可预测的。
让我们使用“random”函数从标准正态分布中采样来模拟随机游走。
# 没有漂移的随机行走
np.rao.sed(1)
n = 1000
x = w = np.aonral(size=n)
for t in rnge(_sples):
x\[t\] = x\[t-1\] + w\[t\]
splt(x, las=30)无漂移的随机行走
显然,我们的 TS 不是平稳的。让我们看看随机游走模型是否适合我们的模拟数据。回想一下随机游走是xt = xt-1 + wt。使用代数我们可以说xt - xt-1 = wt。因此,我们随机游走系列的第一个差异应该等于白噪声过程,我们可以在我们的 TS 上使用“ np.diff()” 函数,看看这是否成立。
# 模拟的随机游走的第一个差值
plt(p.dffx), las=30)随机行走的一阶差分
我们的定义成立,因为这看起来与白噪声过程完全一样。如果我们对 SPY 价格的一阶差分进行随机游走会怎么样?
# SPY价格的一阶差分
plt(diff(dt.PY), lag=30)将随机行走模型拟合到ETF价格
它与白噪声非常相似。但是,请注意 QQ 和概率图的形状。这表明该过程接近正态分布,但具有“重尾”。 ACF 和 PACF 在滞后 1、5?、16?、18 和 21 附近似乎也存在一些显着的序列相关性。这意味着应该有更好的模型来描述实际的价格变化过程。
线性模型
线性模型又称趋势模型,代表了一个可以用直线作图的TS。其基本方程为。 
在这个模型中,因变量的值由β系数和一个单一的自变量--时间决定。一个例子是,一家公司的销售额在每个时间段都会增加相同的数量。 让我们来看看下面的一个特制的例子。在这个模拟中,我们假设坚定的ABC公司在每个时间段的销售额为-50.00元(β0或截距项)和+25.00元(β1)。
# 模拟线性趋势
# 例子 公司ABC的销售额默认为-50元,在每个时间步长为+25元
w = n.anom.ann(100)
y = nppt_lke(w)
b0 = -50.
b1 = 25.
for t in rge(lnw)):
y\[t\] = b0 + b1*t + w\[t\]
plt(y, lags=ls)线性趋势模型模拟
在这里我们可以看到模型的残差是相关的,并且作为滞后的函数线性减少。分布近似正态。在使用此模型进行预测之前,我们必须考虑并消除序列中存在的明显自相关。PACF 在滞后 1 处的显着性表明_自回归_ 模型可能是合适的。
对数线性模型
这些模型与线性模型类似,只是数据点形成了一个指数函数,代表了相对于每个时间步的恒定变化率。例如,ABC公司的销售额在每个时间步长增加X%。当绘制模拟的销售数据时,你会得到一条看起来像这样的曲线。
# 模拟ABC的指数式增长
# 日期
pdat_rge('2007-01-01', '2012-01-01', freq='M')
# 假设销售额以指数速度增长
ale = \[exp( x/12 ) for x inage1, len(id)+1)\]
# 创建数据框架并绘图
df = d.ataame(sals, ix=x)
plt()模拟指数函数
然后我们可以通过采用销售额的自然对数来转换数据。现在线性回归拟合数据。
# ABC对数销售
indexid.plot()指数函数的自然对数
如前所述,这些模型有一个致命的弱点。它们假设连续不相关的误差,正如我们在线性模型的例子中看到的那样。在现实生活中,TS数据通常会违反我们的平稳假设,这使我们转向自回归模型。
自回归模型 - AR(p)
当因变量针对自身的一个或多个滞后值进行回归时,该模型称为自回归模型。公式如下所示:
AR (P) 模型
当您描述 模型的“阶”时,例如阶“p”的 AR 模型, p 表示模型中使用的滞后变量的数量。例如,AR(2) 模型或_二阶_自回归模型如下所示:
AR (2) 模型
这里,alpha (a) 是系数,omega (w) 是白噪声项。在 AR 模型中,Alpha 不能等于 0。请注意,alpha 设置为 1 的 AR(1) 模型是_随机游走_ ,因此不是平稳的。
AR(1) 模型,ALPHA = 1;随机漫步
让我们模拟一个 alpha 设置为 0.6 的 AR(1) 模型
# 模拟一个α=0.6的AR(1)过程
rndm.sed(1)
n_sams = int(1000)
a = 0.6
x = w = n.amma(siz=_apes)
for t in rane(n_saps):
x\[t\] = a*x\[t-1\] + w\[t\]
plot(x, gs=lgs)AR(1) 模型,ALPHA = 0.6
正如预期的那样,我们模拟的 AR(1) 模型的分布是正常的。滞后值之间存在显着的序列相关性,尤其是在滞后 1 处,如 PACF 图所示。
现在我们可以使用 Python 的 statsmodels 拟合 AR(p) 模型。首先,我们将 AR 模型拟合到我们的模拟数据并收益估计的 alpha 系数。然后我们使用 statsmodels 函数“order()”来查看拟合模型是否会选择正确的滞后。如果 AR 模型是正确的,估计的 alpha 系数将接近我们的真实 alpha 0.6,所选阶数等于 1。
# 拟合AR(p)模型到模拟的AR(1)模型,alpa=0.6
md = AR(x).itm=30, ic='aic', trnd='nc')
%time st_oer = mt.R(x).stor(
mxag=30, ic='aic', trnd='nc')
tuerer = 1看起来我们能够恢复模拟数据的基础参数。让我们用 alpha\_1 = 0.666 和 alpha\_2 = -0.333 来模拟 AR(2) 过程。为此,我们使用 statsmodel 的“generate_samples()”函数。该函数允许我们模拟任意阶数的 AR 模型。
# 模拟一个AR(2)过程
n = int(1000)
# Python要求我们指定零滞后值,即为1
# 还要注意,AR模型的字母必须是否定的
# 对于AR(p)模型,我们也将MA的betas设置为0
ar = nr_\[1, -ahas\]
ma = npr_\[1, beas\]
ar2 = smt.arme_pe(ar=ar, ma=a, nsale=n)
plot(ar2, lags=lags)AR(2) 模拟 ALPHA\_1 = 0.666 和 ALPHA\_2 = -0.333
让我们看看是否可以恢复正确的参数。
# 拟合AR(p)模型来模拟AR(2)过程
max_lag = 10
est_rer = st.AR(r2)sennc')
tu_rder = 2让我们看看 AR(p) 模型将如何拟合 MSFT 对数收益。这是收益TS。
MSFT 对数收益时间序列
# 选择MSFT收益的最佳滞后阶数
max_ag = 30
ml = smt.AR(ls.MSFT).fit(mam_lg, c='aic', tnc)
es_rr = tAR(rts.FT).secter(
maag=malag ic=aic', re=nc')
p('最佳估计滞后阶数 = {}'.format(etoer))最好的阶数是 23 个滞后或 23 !任何具有这么多参数的模型在实践中都不太可能有用。显然,收益过程背后的复杂性比这个模型所能解释的要复杂得多。
移动平均模型 - MA(q)
MA(q) 模型与 AR(p) 模型非常相似。不同之处在于 MA(q) 模型是过去白噪声误差项的线性组合,而不是像 AR(p) 模型这样的过去观察的线性组合。MA 模型的目的是我们可以通过将模型拟合到误差项来直接观察误差过程中的“冲击”。在 AR(p) 模型中,通过使用 ACF 对过去的一系列观察结果间接观察到这些冲击。MA(q) 模型的公式是:
Omega (w) 是 E(wt) = 0 且方差为 sigma 平方的白噪声。让我们使用 beta=0.6 并指定 AR(p) alpha 等于 0 来模拟这个过程。
# 模拟一个MA(1)过程
n = int(1000)
# 设置AR(p)的alphas等于0
alpas = npray(\[0.\])
beas = np.ra(\[0.6\])
# 添加零滞后
ar = np_\[1, -alph\]
ma = np_\[1, beta\]
a1 = st.m_gerse(ar=ar, ma=a, naple=n)
plot(ma1, lags=30)BETA=0.6 的模拟 MA(1) 过程
ACF 函数显示滞后 1 很重要,这表明 MA(1) 模型可能适用于我们的模拟序列。当 ACF 仅在滞后 1 处显示显着性时,我不确定如何解释在滞后 2、3 和 4 处显示显着性的 PACF。我们现在可以尝试将 MA(1) 模型拟合到我们的模拟数据中。我们可以使用 “ARMA()” 函数来指定我们选择的阶数。我们调用它的“fit()” 方法来返回模型输出。
# 将MA(1)模型与我们模拟的时间序列相匹配
# 指定ARMA模型,阶数为(p,q)。
maxlag = 30
st.RMa1, orer=(0,1)).fit
maag=maxg, ethod='e', tren='nc')MA(1) 模型概要
该模型能够正确估计滞后系数,因为 0.58 接近我们的真实值 0.6。另请注意,我们的 95% 置信区间确实包含真实值。让我们尝试模拟 MA(3) 过程,然后使用我们的 ARMA 函数将三阶 MA 模型拟合到系列中,看看我们是否可以恢复正确的滞后系数(β)。Beta 1-3 分别等于 0.6、0.4 和 0.2。
# 模拟MA(3)过程,beta为0.6, 0.4, 0.2
n = nt(100)
ar = nr_\[1, -ahas\]
ma = np.r_\[1, betas\]
m3 = genrae_sle(ar=ar, ma=ma, sple=n)
plot(ma3, las=30)BETAS = [0.6, 0.4, 0.2] 的模拟 MA(3) 过程
# 将MA(3)模型拟合模拟的时间序列
maxlg = 30
ARMA(ma3, order=(0, 3)).fit(
xla=mx_ag, mehd='le',tred=nc').summaryMA(3) 模型总结
该模型能够有效地估计实际系数。我们的 95% 置信区间还包含 0.6、0.4 和 0.3 的真实参数值。现在让我们尝试将 MA(3) 模型拟合到 SPY 的对数收益。请记住,我们不知道_真正的_参数值。
# 将MA(3)与SPY收益拟合
x_ag = 30
Y = lrsSY
ARMA(Y, ordr=(0, 3)).it(
mlg=m_lg, thd'le', rndn'.summry())
plot(md.rsd lgs=m_lg)SPY MA (3) 模型总结
让我们看看模型残差。
不错。一些 ACF 滞后有点问题,尤其是在 5、16 和 18 处。这可能是采样错误,但再加上重尾,我认为这不是预测未来 SPY收益的最佳模型。
自回归移动平均模型 - ARMA(p, q)
ARMA 模型只是 AR(p) 和 MA(q) 模型之间的合并。让我们从量化金融的角度回顾一下这些模型对我们的意义:
- AR(p) 模型试图捕捉_(解释)_交易市场中经常观察到的动量和均值回归效应。
- MA(q) 模型试图捕捉_(解释)_在白噪声项中观察到的冲击效应。这些冲击效应可以被认为是影响观察过程的意外事件,例如意外收益、恐怖袭击等。
“对于杂货店中的一组产品,在不同时间推出的有效优惠券活动的数量将构成多重‘冲击’,从而影响相关产品的价格。”
ARMA 的弱点在于它忽略了在大多数金融时间序列中发现的_波动性聚类_效应。
模型公式为:
ARMA(P, Q) 方程
让我们用给定的参数模拟一个 ARMA(2, 2) 过程,然后拟合一个 ARMA(2, 2) 模型,看看它是否可以正确估计这些参数。设置 alpha 等于 [0.5,-0.25] 和 beta 等于 [0.5,-0.3]。
# 模拟一个ARMA(2, 2)模型,alphas=\[0.5,-0.25\],betas=\[0.5,-0.3\]
max_lag = 30
n = int(5000) #大量的样本来帮助估算
burn = int(n/10) #拟合前要丢弃的样本数
ar = np.r_\[1, -alphas\]
ma = np.r_\[1, betas\]
aa22 = aample(ar=ar, ma=ma,samle=n)
plt(rm2, lagsxla)
ARMA(arma22, order=(2, 2)).fit(
maxag=ma_lag, mtd='mle', ted='nc', brnn=brn).summry()模拟 ARMA(2, 2) 过程
ARMA(2, 2) 模型总结
我们的真实参数包含在 95% 的置信区间内。
接下来我们模拟一个 ARMA(3, 2) 模型。之后,我们循环使用 p、q 的组合,以将 ARMA 模型拟合到我们的模拟序列中。我们根据哪个模型产生最低值来选择最佳组合Akaike Information Criterion (AIC)").
# 模拟一个ARMA(3, 2)模型,alphas=\[0.5,-0.25,0.4\],betas=\[0.5,-0.3\] 。
maxg = 30
n = int(5000)
burn = 2000
alpas = nparay(\[0.5, -0.25, 0.4\])
bets = np.ra(\[0.5, -0.3\])
ar = np.r_\[1, -alas\]
ma = np.r_\[1, betas\]
arma32 = armasamp(ar=ar, ma=ma, nsple=n, rin=burn)
plot(ara32, lgs=mxlg)
# 通过AIC选择最佳阶数
# 最小的AIC值最优
for i in rn:
for j in rn:
try:
tmpl = ARMA(arma32, orde=(i, j)).fit(meod='mle', tend='nc')
aic = tp_ml.ac
if tmpaic < bstaic:
bst\_ic = mp\_aic
bestrder = (i, j)
bes_mdl = tmpdl
excpt: ctinue![]()
上面恢复了正确的阶数。下面我们看到了在任何模型拟合之前模拟时间序列的输出。
模拟 ARMA(3, 2) 系列,其中 Alpha = [0.5,-0.25,0.4] 和 BETAS = [0.5,-0.3]
ARMA(3, 2) 最佳模型总结
我们看到选择了正确的阶数并且模型正确地估计了我们的参数。但是请注意 MA.L1.y 系数;0.5 的真实值几乎在 95% 的置信区间之外!
下面我们观察模型的残差。显然这是一个白噪声过程,因此最好的模型已经被拟合来_解释_ 数据。
ARMA(3, 2) 最佳模型残差白噪声
接下来,我们将 ARMA 模型拟合到 SPY 收益。下图是模型拟合前的时间序列。
SPY收益率
# 将ARMA模型与SPY收益率拟合
rng = rng(5) # \[0,1,2,3,4,5\]
for i in rng:
for j in rng:
try:
tmp_mdl = ARMA('SPY', oder=(i, j))fit
tmp\_ic = tp\_dl.aic
if tp\_ic < bes\_aic:
bs\_aic = mp\_aic
es_der = (i j)
bst\_mdl = t\_mdl
exet: cntnue![]()
我们绘制模型残差。
SPY最佳模型残差 ARMA(4, 4)
ACF 和 PACF 没有显示出显着的自相关。QQ 和概率图显示残差近似正态并带有重尾。然而,这个模型的残差看起来不像白噪声,可以看到模型未捕获的明显条件异方差(_条件波动性_)的突出显示区域。
自回归综合移动平均模型 - ARIMA(p, d, q)
ARIMA是ARMA模型类别的自然延伸。如前所述,我们的许多TS并不是平稳的,但是它们可以通过差分而成为平稳的。我们看到了一个例子,当我们采取Guassian随机游走的第一次差分,并证明它等于白噪声。换句话说,我们采取了非平稳的随机行走,并通过第一次差分将其转变为平稳的白噪声。
不用太深入地研究这个方程,只要知道 "d "是指我们对序列进行差分的次数。顺便提一下,在Python中,如果我们需要对一个序列进行多次差分,我们必须使用np.diff()函数。pandas函数DataFrame.diff()/Series.diff()只处理数据帧/序列的第一次差分,没有实现TSA中需要的递归差分。
在下面的例子中,我们通过(p, d, q)订单的非显著数量的组合进行迭代,以找到适合SPY收益的最佳ARIMA模型。我们使用AIC来评估每个模型。最低的AIC获胜。
# 将ARIMA(p, d, q)模型适用于SPY收益
# 根据AIC选择最佳阶数和最终模型
for i in prng:
for d in rng:
for j in prng:
try:
tp_dl = ARIMAfit(lrs, orer=(i,d,j))
if tpaic < betaic:
bestic = tmp_ic
bes_orer = (i, d, j)
bestl = tpmdl
# ARIMA模型的残差图
plot(resid, lags=30)最好的模型的差值为 0 也就不足为奇了。回想一下,我们已经用对数价格的第一个差值来计算股票收益。下面,我绘制了模型残差。结果与我们上面拟合的 ARMA(4, 4) 模型基本相同。显然,这个 ARIMA 模型也没有解释序列中的条件波动!
拟合SPY收益的 ARIMA 模型
现在我们至少积累了足够的知识来对未来的收益进行简单的预测。这里我们使用我们模型的predict() 方法。作为参数,要预测的时间步数需要一个整数,alpha 参数需要一个小数来指定置信区间。默认设置为 95% 置信度。对于 99%,设置 alpha 等于 0.01。
# 创建一个具有95%、99%CI的21天SPY收益预测
n_steps = 21
fc9 =atFae(ncolmack(\[c99\])
inx=clus=\['wr\_ci99', upr\_ci_99')
fc_ll.head(# 绘制21天的SPY收益预测图
ilc\[-500:\].cpy()
# 在样本预测中
prdct(side\[0\], t.id\[-1\])
plt(ax=x, stye=styes)21 天SPY收益预测 - ARIMA(4,0,4)
自回归条件异方差模型 - ARCH(p)
ARCH(p) 模型可以简单地认为是应用于时间序列方差的 AR(p) 模型。另一种思考方式是,我们的时间序列 _在时间 t_的方差取决于对先前时期方差的过去观察。
ARCH(1) 模型公式
假设系列的均值为零,我们可以将模型表示为:
零均值的 ARCH(1) 模型
# 模拟ARCH(1)序列
# Var(yt) = a\_0 + a\_1\*y{t-1}\*\*2
# 如果a_1在0和1之间,那么yt就是白噪声
Y = np.epy_lik
for t in rng(ln()):
Y\[t\] = w\[t * sqrt((a0 + a1\*y\[t-1\*\*2)
# 模拟的ARCH(1)序列,看起来像白噪声
plot(Y, lags=30)模拟ARCH(1)过程
模拟ARCH(1)**2 过程
请注意 ACF 和 PACF 似乎在滞后 1 处显示显着性,表明方差的 AR(1) 模型可能是合适的。
广义自回归条件异方差模型 - GARCH(p,q)
简单地说,GARCH(p, q) 是一个应用于时间序列方差的 ARMA 模型,即它有一个自回归项和一个移动平均项。AR(p) 对残差的方差(平方误差)或简单地对我们的时间序列平方进行建模。MA(q) 部分对过程的方差进行建模。基本的 GARCH(1, 1) 公式是:
GARCH(1, 1) 公式
Omega (w) 是白噪声,alpha 和 beta 是模型的参数。此外 alpha\_1 + beta\_1 必须小于 1,否则模型不稳定。我们可以在下面模拟一个 GARCH(1, 1) 过程。
# 模拟一个GARCH(1, 1)过程
n = 10000
w = rnom.ral(sze=n)
eps = np.er_ike(w)
gsq =pzslie(w)
for i in rne1, n):
sis\[i\] = a+ a1*(eps\[i-1\]\*\*2) + b1\*siq\[i-1\]
es\[i\] = w\[i\] * srt(sisq\[i\])模拟 GARCH(1, 1) 过程
再次注意到,总体上这个过程与白噪声非常相似,然而当我们查看平方的eps序列时,请看一下。
模拟 GARCH(1, 1) 过程平方
显然存在着自相关,ACF和PACF的滞后期的重要性表明我们的模型需要AR和MA。让我们看看我们是否能用GARCH(1, 1)模型恢复我们的过程参数。这里我们使用ARCH包中的arch_model函数。
# 将GARCH(1, 1)模型与我们模拟的EPS序列相匹配
# 我们使用arch函数
am = arch(ps)
fit(dae_freq=5)
summary())GARCH 模型拟合摘要
现在让我们运行一个使用 SPY 收益的示例。过程如下:
- 迭代 ARIMA(p, d, q) 模型的组合来拟合我们的时间序列。
- 根据 AIC 最低的 ARIMA 模型选择 GARCH 模型阶数。
- 将 GARCH(p, q) 模型拟合到我们的时间序列。
- 检查模型残差和残差平方的自相关
另请注意,我选择了一个特定的时间段来更好地突出关键点。然而,根据研究的时间段,结果会有所不同。
for i in pq_g:
for d in d_ng:
for j in p_ng:
try:
tpml = ARIMA(T,order(i,d,j).fi
if tmp\_aic < best\_aic:
best_ic =mpac
best_oder = (i, d, j)
best\_ml =tm\_ml
# 注意我已经选择了一个特定的时间段来运行这个分析
bstmoel(TS)拟合SPY收益的 ARIMA(3,0,2) 模型的残差
看起来像白噪声。
拟合SPY收益的 ARIMA(3,0,2) 模型的平方残差
平方残差显示自相关。让我们拟合一个 GARCH 模型。
# 现在我们可以使用最适合的arima模型参数来拟合arch模型
p_ = bst_dr
o= st_orde
q = bst_er
# 使用学生T分布通常能提供更好的拟合
arcd(TS, p=p_, o=o_, q=q_, 'StdensT')
fit(uat_eq=5, sp='ff')
summaryGARCH(3, 2) 模型拟合SPY收益
在处理非常小的数字时,会出现收敛警告。在必要时,将数字乘以10倍的系数以扩大幅度,可以起到帮助作用,但是对于这个演示来说,没有必要这样做。下面是模型的残差。
拟合SPY收益的 GARCH(3, 2) 模型残差
上面看起来像白噪声。现在让我们查看平方残差的 ACF 和 PACF。
我们已经实现了良好的模型拟合,因为平方残差没有明显的自相关。
最受欢迎的见解
1.HAR-RV-J与递归神经网络(RNN)混合模型预测和交易大型股票指数的高频波动率
2.R语言中基于混合数据抽样(MIDAS)回归的HAR-RV模型预测GDP增长回归的HAR-RV模型预测GDP增长")
4.R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测