二值图像分析:OpenCV中的二值化阈值操作
二值图像分析:OpenCV中的二值化阈值操作
-
- 1.二值图像的定义
- 2.OpenCV中的基本阈值操作
- 3.OTSU二值寻找算法
-
- 3.1 OTSU二值寻找算法介绍
- 3.2 OTSU二值寻找算法分析
- 3.2 OpenCV中OTSU算法的使用
- 4.TRIANGLE二值寻找算法
-
- 41 TRIANGLE二值寻找算法介绍
- 4.2 TRIANGLE二值寻找算法分析
- 4.3 OpenCV中TRIANGLE算法的使用
- 5.自适应二值化阈值算法
1.二值图像的定义
二值图像就是图像中灰度值只有2个的图像,一般就是黑白图像,2个灰度值分别为0(表示黑色)和255(表示白色)。二值图像处理与分析在机器视觉与机器人视觉中非常重要,涉及到非常多的图像处理相关的知识。
常见的二值图像分析包括轮廓分析、对象测量、轮廓匹配与识别、形态学处理与分割、各种形状检测与拟合、投影与逻辑操作、轮廓特征提取与编码等。此外图像二值化的方法也有很多,OpenCV支持几种经典的二值化算法。
从编程与代码角度来说,OpenCV中二值图像是单通道的、字节类型的Mat对象。对于任意的输入图像首先需要把图像转换为灰度图,然后通过二值化方法转换为二值图像。本质上来说,从灰度到二值图像是对数据的二分类分割,所以很多数据处理的方法都可以使用,但是图像是特殊类型的数据,它有很多限制条件,这决定了只有一些合适的方法才会取得比较好的效果。这些方法的本质任务就是寻找合理的分割阈值T,使得对于任意一个给定的像素点灰度值经过如下变换成为0或255其中的一个:
P ( x , y ) = { 255 , P ( x , y ) > T . 0 , P ( x , y ) ≤ T . P(x, y) = \begin{cases} 255, \qquad & P(x, y) \gt T. \\ 0, \qquad & P(x, y) \le T. \end{cases} P(x,y)={ 255,0,P(x,y)>T.P(x,y)≤T.
2.OpenCV中的基本阈值操作
如果已经寻找到合适的阈值T,那么对图像二值化分割可以看成是一种基本的阈值化操作,OpenCV除了支持正常的二值化阈值分割操作之外,还支持一些其它的阈值操作。
OpenCV中支持的基本阈值操作的C++ API如下:
double cv::threshold(
InputArray src,
OutputArray dst,
double thresh,
double maxval,
int type)
其中src为单通道的输入图像,dst为输出的二值图像,maxval为最大值,一般为255,thresh为阈值,可以与type表示的阈值分割方法配合使用产生不同的二值化效果,type在基本二值化时支持如下五种:
THRESH_BINARY = 0:正向二值分割,大于阈值为maxval,反之为0。THRESH_BINARY_INV = 1:反向二值分割,大于阈值为0,反之为maxval。THRESH_TRUNC = 2:截断,大于阈值时设为为阈值,否则保持原值不改变。THRESH_TOZERO = 3:取零,大于阈值保留原值不变,低于阈值为0。THRESH_TOZERO_INV = 4:反向取零,大于阈值时设为0,否则保持原值不变。
返回值double类型用于返回实际使用的阈值,因为threshold不仅可以用给定的阈值,也支持一些自动生成阈值的二值化方法,这个时候就可以用这个返回值来得到自动方法所生成的阈值。
举个栗子:
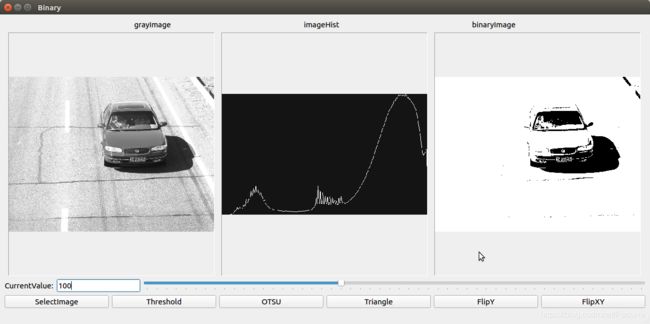
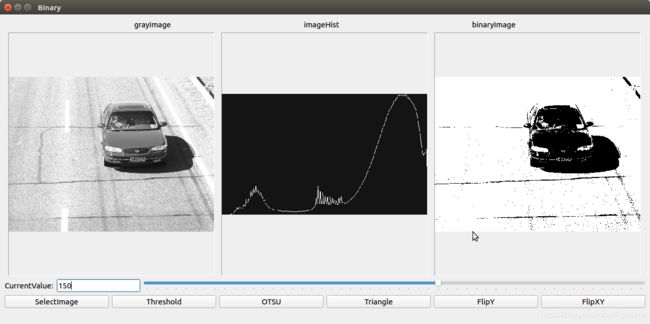
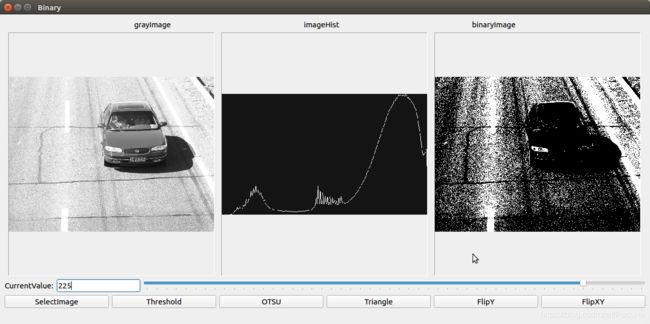
cv::threshold(grayImage,binaryImage,value,255.0,0);
指定二值化方法为THRESH_BINARY = 0时,几个不同阈值时的二值化效果如下:
图像二值化除了第二部分中的手动阈值设置方法之外,还有几个根据图像直方图实现自动全局阈值寻找的方法。OpenCV中支持的有OTSU与Triangle这两种直方图阈值寻找算法,这两个非常具有代表性,可以覆盖常见的直方图分布图像。
3.OTSU二值寻找算法
3.1 OTSU二值寻找算法介绍
OTSU是通过计算类间最大方差(找到一个阈值 k k k 将像素灰度值分为2类,使得这2个类的类间方差最大)来确定分割阈值的阈值选择算法,该算法针对图像直方图来计算阈值,对有两个波峰(前景对象和背景)、中间有明显波谷的直方图对应的图像二值化效果比较好,而对于只有一个单峰的直方图对应的图像分割效果没有双峰的好。
3.2 OTSU二值寻找算法分析
假设一幅图像大小为 M ∗ N M*N M∗N,像素值属于集合 { 0 , 1 , 2 , . . . , 255 } \{0,1,2,...,255\} { 0,1,2,...,255},用 n i n_i ni 表示像素值为 i i i 的像素点的个数,由此可以得到图像的归一化直方图,直方图横轴分量 p i = n i / M N p_i=n_i/MN pi=ni/MN ,由概率和统计知识可以得到:
像 素 总 数 M ∗ N = n 0 + n 1 + . . . + n 255 . (1) 像素总数M*N=n_0+n_1+...+n_{255}.\tag{1} 像素总数M∗N=n0+n1+...+n255.(1)
∑ i = 0 255 p i = 1 , p i ≥ 0. (2) \sum_{i=0}^{255}p_i=1,p_i\geq0.\tag{2} i=0∑255pi=1,pi≥0.(2)
首先来看对于任意一个给定的介于 0~255的阈值 k k k,将其作为图像阈值来对图像进行二值化操作,可以将像素灰度值分为背景 C 1 C_1 C1 和前景对象 C 2 C_2 C2两个类,其中 C 1 C_1 C1由图像中灰度值在区间 [0, k k k] 的所有像素组成, C 2 C_2 C2由图像中灰度值在区间 [ k k k+1,255] 的所有像素组成。
则此图像中,像素被分到 C 1 C_1 C1的概率(或者说 C 1 C_1 C1发生的概率)由如下的累计和给出:
P 1 ( k ) = ∑ i = 0 k p i . (3) P_1(k)=\sum_{i=0}^{k}p_i.\tag{3} P1(k)=i=0∑kpi.(3)
像素被分到 C 2 C_2 C2的概率(或者说 C 2 C_2 C2发生的概率)由如下的累计和给出:
P 2 ( k ) = ∑ i = k + 1 255 p i = 1 − P 1 ( k ) . (4) P_2(k)=\sum_{i=k+1}^{255}p_i=1-P_1(k).\tag{4} P2(k)=i=k+1∑255pi=1−P1(k).(4)
分配到 C 1 C_1 C1类的平均像素值为:
m 1 ( k ) = ∑ i = 0 k i ⋅ P ( i / C 1 ) = ∑ i = 0 k i ⋅ P ( C 1 / i ) P ( i ) / P ( C 1 ) = 1 P 1 ( k ) ∑ i = 0 k i ⋅ p i (5) m_1(k)=\sum_{i=0}^{k}i·P(i/C_1)\\\qquad\qquad=\sum_{i=0}^{k}i·P(C_1/i)P(i)/P(C_1)\\={\frac{1}{P_1(k)}}{\sum_{i=0}^{k}i·p_i}{\tag{5}} m1(k)=i=0∑ki⋅P(i/C1)=i=0∑ki⋅P(C1/i)P(i)/P(C1)=P1(k)1i=0∑ki⋅pi(5)
上式中第二行可由贝叶斯公式得到,而在第三行中,在给定 i i i 的前提下 C 1 C_1 C1 发生的概率 P ( C 1 / i ) P(C_1/i) P(C1/i) 为1, P ( i ) P(i) P(i) 是第 i i i 个值的概率,即归一化直方图 p i p_i pi 分量的第 i i i 个分量, P ( C 1 ) P(C_1) P(C1) 是 C 1 C_1 C1 发生的概率,等于(3)式中计算得到的 P 1 ( k ) P_1(k) P1(k)。
同理,分配到 C 2 C_2 C2类的平均像素值为:
m 2 ( k ) = ∑ i = k + 1 255 i ⋅ P ( i / C 2 ) = 1 P 2 ( k ) ∑ i = k + 1 255 i ⋅ p i (6) m_2(k)=\sum_{i=k+1}^{255}i·P(i/C_2)\\\qquad\qquad=\frac{1}{P_2(k)}\sum_{i=k+1}^{255}i·p_i{\tag{6}} m2(k)=i=k+1∑255i⋅P(i/C2)=P2(k)1i=k+1∑255i⋅pi(6)
整个图像的平均像素值为:
m G = ∑ i = 0 255 i ⋅ p i (7) m_G=\sum_{i=0}^{255}i·p_i{\tag{7}} mG=i=0∑255i⋅pi(7)
为了评估k的分类质量,假设 σ G 2 \sigma_G^2 σG2为全局方差,即图像中所有像素灰度值的方差,该值是一个常数且只需要计算一次。 σ B 2 \sigma_B^2 σB2为类间方差,则有:
σ G 2 = ∑ i = 0 255 ( i − m G ) 2 ⋅ p i (8) \sigma_G^2=\sum_{i=0}^{255}(i-m_G)^2·p_i{\tag{8}} σG2=i=0∑255(i−mG)2⋅pi(8)
σ B 2 = P 1 ( m 1 − m G ) 2 + P 2 ( m 2 − m G ) 2 = P 1 P 2 ( m 1 − m 2 ) 2 = ( m G P 1 − m ) 2 P 1 ( 1 − P 1 ) (9) \sigma_B^2=P_1(m_1-m_G)^2+P_2(m_2-m_G)^2{\tag{9}}\\=P_1P_2(m_1-m_2)^2\\=\frac{ {(m_GP_1-m)}^2}{P_1(1-P_1)} σB2=P1(m1−mG)2+P2(m2−mG)2=P1P2(m1−m2)2=P1(1−P1)(mGP1−m)2(9)
至此对于给定的 k k k,已经可以求出此时两个类的类间方差,那么接下来要做的就是对于0~255之间每一个可能的 k k k 按照上面的方式来计算类间方差,找到使其最大化的那一个,如果能使类间方差最大的 k k k 值有多个,则一般取这些 k k k 的平均值。
3.2 OpenCV中OTSU算法的使用
OpenCV中OTSU算法使用只需要在threshold()函数的type类型声明THRESH_OTSU即可,举个栗子:
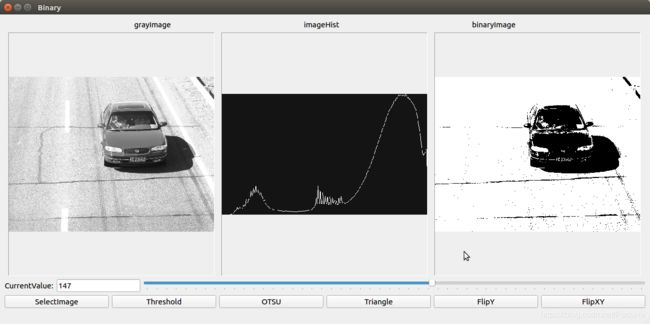
double t = threshold(gray,binary,0,255,THRESH_BINARY|THRESH_OTSU);
同样对于上面的图,计算得到的阈值为147,运行结果如下:
4.TRIANGLE二值寻找算法
41 TRIANGLE二值寻找算法介绍
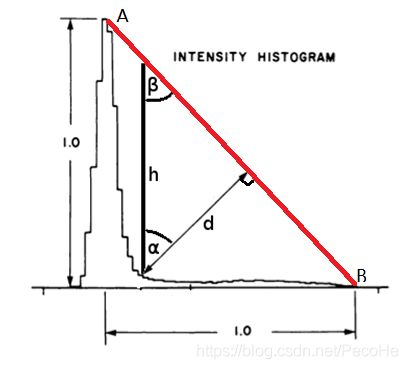
对于直方图为双波峰的图像来说,是比较好的二值化方法。而对于直方图为单波峰的图像来说,三角阈值法更为有效。之所以叫三角阈值法,是因为该算法通过在图像直方图上构建一个三角形来获得阈值。
4.2 TRIANGLE二值寻找算法分析
对于该图像的直方图,首先引一条直线,即图中的红色线,使得该直线经过波峰最高点 A A A 和横轴最远点 B B B,然后不断地作该条直线的垂线,找到使得 d d d 最大化就可以了。实际上可以通过构造等腰直角三星形(如图, α α α 和 β β β 都是45度)来寻找最大 d d d ,则寻找最大 d d d 等价于寻找最大 h h h,显然 h h h 更好找。经 h h h 计算得到的 d d d 就是本算法寻找到的阈值。
h 2 = 2 ⋅ d 2 − > d = s q r t ( h 2 2 ) . h^2=2·d^2->d=sqrt(\frac{h^2}{2}). h2=2⋅d2−>d=sqrt(2h2).
这里有一个细节,就是对于上面的直方图,该直方图波峰是在靠0的位置,偏左侧。如果实际直方图波峰是靠1.0(不归一化是255),偏右侧的时候,则可以对所有像素取反,然后按照之前的方式来处理就可以了。
4.3 OpenCV中TRIANGLE算法的使用
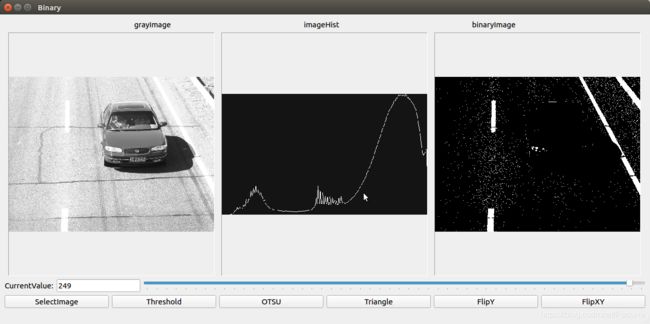
OpenCV中TRIANGLE算法使用只需要在threshold()函数的type类型声明THRESH_TRIANGLE即可,举个栗子:
double t = threshold(gray,binary,0,255,THRESH_BINARY|THRESH_TRIANGLE);
同样对于上面的图,计算得到的阈值为249,运行结果如下:
5.自适应二值化阈值算法
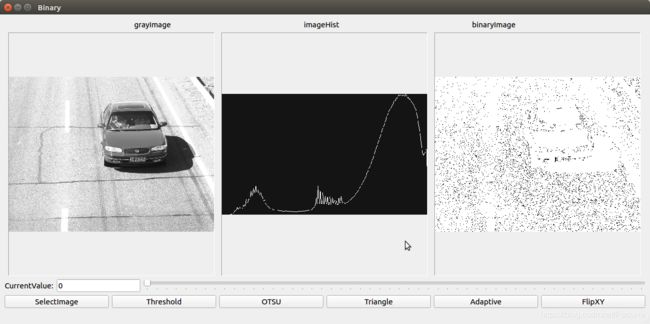
OpenCV中的自适应阈值算法主要是基于均值实现,根据计算均值的方法不同分为盒子模糊(box filter)均值与高斯模糊均值,然后使用原图减去均值图像,得到的差值图像进行自适应分割,相关的API如下:
void cv::adaptiveThreshold(
InputArray src,
OutputArray dst,
double maxValue,
int adaptiveMethod,
int thresholdType,
int blockSize,
double C)
其中blockSize取值必须是奇数,C取值在10左右
adaptiveMethod自适应方法类型:
ADAPTIVE_THRESH_GAUSSIAN_C = 1:ADAPTIVE_THRESH_MEAN_C = 0:
当阈值操作类型thresholdType为:
THRESH_BINARY:二值图像 = 原图–均值图像> C? 255:0。THRESH_BINARY_INV:二值图像 = 原图–均值图像>C? 0:255。
举个栗子:
cv::adaptiveThreshold(grayImage,binaryImage,255.0,cv::ADAPTIVE_THRESH_GAUSSIAN_C,cv::THRESH_BINARY,3,10.0);