在K-Means算法中使用肘部法寻找最佳聚类数
1.from scipy.cluster.vq import kmeans包的介绍:
输入 数据集和簇的数量
返回 聚类中心坐标(codebook)、观测值与生成的质心之间的平均(非平方)欧氏距离(distortion)
例1:
import numpy as np
from scipy.cluster.vq import vq, kmeans, whiten
import matplotlib.pyplot as plt
features = np.array([[1,1],
[2,2],
[3,3],
[4,4],
[5,5]])
wf = whiten(features)
print("whiten features: \n", wf)
book = np.array((wf[0], wf[1]))
codebook, distortion = kmeans(wf, book)
# 可以写kmeans(wf,2), 2表示两个质心,同时启用iter参数
print("codebook:", codebook)
print("distortion: ", distortion)
plt.scatter(wf[:,0], wf[:,1])
plt.scatter(codebook[:, 0], codebook[:, 1], c='r')
plt.show()结果:
whiten features:
[[0.70710678 0.70710678]
[1.41421356 1.41421356]
[2.12132034 2.12132034]
[2.82842712 2.82842712]
[3.53553391 3.53553391]]
codebook: [[1.06066017 1.06066017]
[2.82842712 2.82842712]]
distortion: 0.5999999999999999例2:
import numpy as np
from scipy.cluster.vq import vq, kmeans, whiten
import matplotlib.pyplot as plt
pts = 5
a = np.random.multivariate_normal([0, 0], [[4, 1], [1, 4]], size=pts)
b = np.random.multivariate_normal([30, 10],
[[10, 2], [2, 10]],
size=pts)#np.random.multivariate_normal这个官方解释说从多元正态分布中抽取随机样本
features = np.concatenate((a, b))
#print(features)
print(features.shape)
whitened = whiten(features)
print(whitened)
codebook, distortion = kmeans(whitened, 2) #这个Kmeans好像只返回聚类中心、观测值和聚类中心之间的失真
plt.scatter(whitened[:, 0], whitened[:, 1],c = 'g')
plt.scatter(codebook[:, 0], codebook[:, 1], c='r')
plt.show()
结果:
(10, 2)
[[-0.01741221 -0.49577372]
[-0.08524789 -0.17768591]
[ 0.0657376 0.47027214]
[ 0.27825025 -0.37835465]
[-0.0079966 0.50196071]
[ 1.824303 2.55040188]
[ 2.05886112 2.08174181]
[ 2.13775252 1.69008105]
[ 2.26411531 1.2035603 ]
[ 1.83463368 0.45632992]]
2.针对鸢尾花数据集的k-means的肘部法优化的聚类
"""Find optimal number of clustres from a Dataset."""
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from scipy.cluster.vq import kmeans
from sklearn.datasets import load_iris
from scipy.spatial.distance import cdist
from scipy.spatial.distance import pdist
def load_dataset():
"""Load dataset."""
# Loading dataset.
return load_iris().data
def find_clusters(dataset):
"""Function to find optimal number of clusters in dataset."""
# cluster data into K=1..10 clusters
num_clusters = range(1, 50)
#从1到50个分别进行聚类,得到50种kmeans的质点坐标和欧式距离
k_means = [kmeans(dataset, k) for k in num_clusters]
# cluster's centroids,得到k_means的质点坐标
centroids = [cent for (cent, var) in k_means]
#计算[ [每个数据点到每个质点的距离] (<-中括号为一个点到每个质点的距离)....] <-指当质心数为某时,所有点到质点距离的集合
clusters_dist = [cdist(dataset, cent, 'euclidean') for cent in centroids]
#argmin:返回每组距离矩阵最小的值的下标。这里每组的意思是一个点到每个质点的距离集合。
# #所以这里用来判断该数据属于哪一类(哪一个质点),并且argmin会将多重数组平铺成一重数组,即每组clusters_dist都会放到同一个数组中,即最后只有50组数组
cidx = [np.argmin(_dist, axis=1) for _dist in clusters_dist]
#返回最短的距离
dist = [np.min(_dist, axis=1) for _dist in clusters_dist]
# Mean within-cluster (sum of squares)
avg_within_sum_sqrd = [sum(d) / dataset.shape[0] for d in dist]
return {'cidx': cidx, 'avg_within_sum_sqrd': avg_within_sum_sqrd,
'K': num_clusters}
def plot_elbow_curv(details):
"""Function to plot elbo curv."""
kidx = 2
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(details['K'], details['avg_within_sum_sqrd'], 'b*-')
ax.plot(details['K'][kidx], details['avg_within_sum_sqrd'][kidx],
marker='o', markersize=12, markeredgewidth=2,
markeredgecolor='r', markerfacecolor='None')
plt.grid(True)
plt.xlabel('Number of clusters')
plt.ylabel('Average within-cluster sum of squares')
plt.title('Elbow for KMeans clustering')
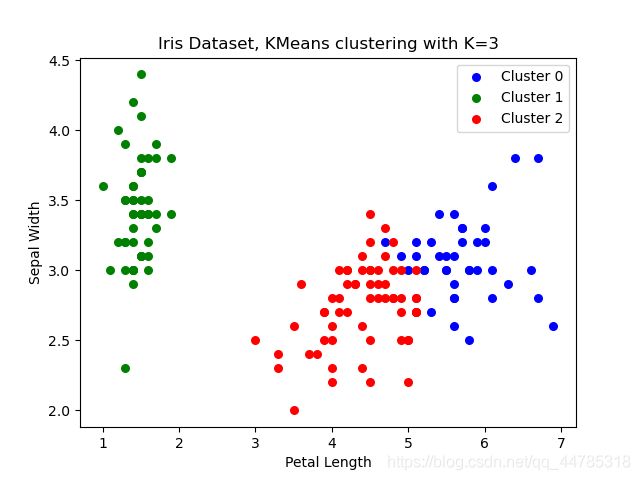
def scatter_plot(dataset, details):
"""Function to plot scatter plot of clusters."""
kidx = 2
fig = plt.figure()
ax = fig.add_subplot(111)
clr = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
#这个循环为质点个数,每次循环代表一个聚落
for i in range(details['K'][kidx]):
#返回Ture或False
#其实就是当前聚落设为True,其余为False。数组读取的只能为True的值
ind = (details['cidx'][kidx] == i)
#数组[Ture,0]指取[0]值,数组[False,0]指不取[0]值
#dataset[ind[index],2]指:取dataset的第二列的每行,其中ind对应行为False时dataset数组不取
ax.scatter(dataset[ind, 2], dataset[ind, 1],
s=30, c=clr[i], label='Cluster %d' % i)
plt.xlabel('Petal Length')
plt.ylabel('Sepal Width')
plt.title('Iris Dataset, KMeans clustering with K=%d' % details['K'][kidx])
plt.legend()
plt.show()
#判断肘点,需肉眼观察,上述kidx的值基于这个函数。n代表聚类个数
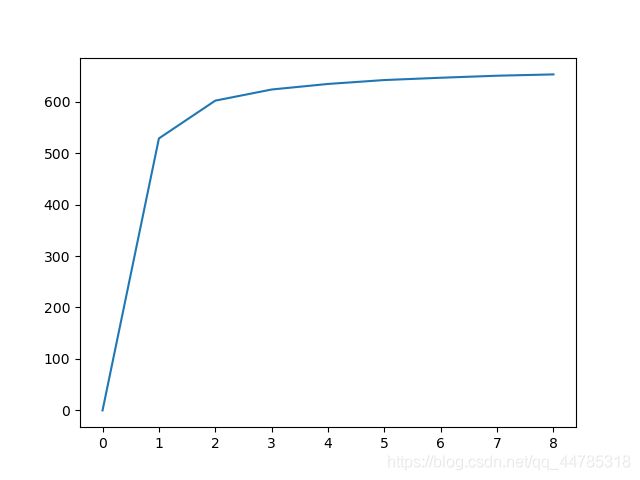
def eblow(n):
"""Elbow testing."""
#测试集的属性
cols = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
df = pd.read_csv('data.csv', usecols=cols).values
#聚类数从1到n-1的模型
kmeans_var = [KMeans(n_clusters=k).fit(df) for k in range(1, n)]
#得到中心点坐标,每个属性看作一维,所以每个中心点坐标有4个值
centroids = [x.cluster_centers_ for x in kmeans_var]
#得到每个数据点到每个中心点的距离
k_euclid = [cdist(df, cent) for cent in centroids]
#得到k_euclid每组最小的值
dist = [np.min(ke, axis=1) for ke in k_euclid]
#每种聚类数对应的最小距离平方和
wcss = [sum(d**2) for d in dist]
#原数据集距离平方和的均值
tss = sum(pdist(df)**2) / df.shape[0]
bss = tss - wcss
plt.plot(bss)
plt.show()
dataset = load_dataset()
details = find_clusters(dataset)
plot_elbow_curv(details)
scatter_plot(dataset, details)
#可以观察到肘点
eblow(10)
结果: