数据结构学习笔记：二叉树的基础知识总结

程序员在面试中，经常会问到关于数据结构的问题，通过对其熟悉程度，判断面试者的编程能力和以往难度，其中二叉树可谓是数据结构知识点中的必问题目，在本篇博客中，我会将所了解的有关二叉树的知识点总结概括。

二叉树的特点

1. 每个节点最多有两棵子数，没有或有一棵也可以。
2. 左子树与右子树有次序，次序不能颠倒。
3. 即使树中某结点只有一棵子树，也要区分左子树还是右子树。

二叉树基本形态

1. 空二叉树
2. 只有一个根结点
3. 根结点只有左子树
4. 根结点只有右子树
5. 根结点既有左子树，又有右子树

特殊二叉树

1. 斜树：所有的结点都只有左子树的二叉树，称之为左斜树，右斜树同理。
2. 满二叉树：每个结点都存在左子树和右子树，所有的叶子都在同一层上。
3. 完全二叉树：每个结点都按数字编号，编号是连续的。

注意：满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树。

二叉树的遍历：

从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问一次且仅被访问一次。

遍历方法主要分为四种：

• 前序遍历：规则是若二叉树为空，则空操作返回。否则先访问根结点，然后遍历左子树，再遍历右子树。（中－》左－》右）
• 中序遍历：规则是若二叉树为空，则空操作返回。否则先从根结点开始（但并不先访问根结点），先遍历左子树，然后访问根结点，最后遍历右子树。（左－》中－》右）
• 后序遍历：规则是若二叉树为空，则空操作返回。否则从左到右线叶子后结点的方式遍历访问左右子树，最后是访问根结点。（左－》右－》中）
• 层序遍历：规则是若二叉树为空，则空操作返回。否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历。再同一层，按从左到右的顺序对结点逐个访问。

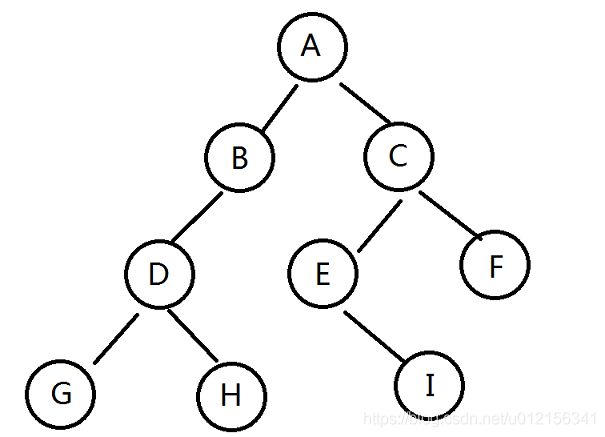
实例：

不同的遍历方法得到的结果并不相同。

前序：A B D G H C E I F                           中序：G D H B A E I C F

后序：G H D B I E F C A                           层序：A B C D E F G H I

不同的遍历提供了对结点依次处理的不同方式，可在遍历过程中对结点进行各种处理。

二叉树排序的代码

package com.animee.work01;
import java.util.LinkedList;
import java.util.List;
public class BinTreeTraverse {  
    private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };  
    private static List nodeList = null;  
    /** 
     * 内部类：节点 
     */  
    private static class Node {  
        Node leftChild;  
        Node rightChild;  
        int data;  
        Node(int newData) {  
            leftChild = null;  
            rightChild = null;  
            data = newData;  
        }  
    }  
    public void createBinTree() {  
        nodeList = new LinkedList();  
        // 将一个数组的值依次转换为Node节点  
        for (int nodeIndex = 0; nodeIndex < array.length; nodeIndex++) {  
            nodeList.add(new Node(array[nodeIndex]));  
        }  
        // 对前lastParentIndex-1个父节点按照父节点与孩子节点的数字关系建立二叉树  
        for (int parentIndex = 0; parentIndex < array.length / 2 - 1; parentIndex++) {  
            // 左孩子  
            nodeList.get(parentIndex).leftChild = nodeList  
                    .get(parentIndex * 2 + 1);  
            // 右孩子  
            nodeList.get(parentIndex).rightChild = nodeList  
                    .get(parentIndex * 2 + 2);  
        }  
        // 最后一个父节点:因为最后一个父节点可能没有右孩子，所以单独拿出来处理  
        int lastParentIndex = array.length / 2 - 1;  
        // 左孩子  
        nodeList.get(lastParentIndex).leftChild = nodeList  
                .get(lastParentIndex * 2 + 1);  
        // 右孩子,如果数组的长度为奇数才建立右孩子  
        if (array.length % 2 == 1) {  
            nodeList.get(lastParentIndex).rightChild = nodeList  
                    .get(lastParentIndex * 2 + 2);  
        }  
    }  
  
    /** 
     * 先序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     *            遍历的节点 
     */  
    public static void preOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        System.out.print(node.data + " ");  
        preOrderTraverse(node.leftChild);  
        preOrderTraverse(node.rightChild);  
    }  
  
    /** 
     * 中序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     *            遍历的节点 
     */  
    public static void inOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        inOrderTraverse(node.leftChild);  
        System.out.print(node.data + " ");  
        inOrderTraverse(node.rightChild);  
    }  
  
    /** 
     * 后序遍历 
     * 这三种不同的遍历结构都是一样的，只是先后顺序不一样而已 
     * @param node 
     *            遍历的节点 
     */  
    public static void postOrderTraverse(Node node) {  
        if (node == null)  
            return;  
        postOrderTraverse(node.leftChild);  
        postOrderTraverse(node.rightChild);  
        System.out.print(node.data + " ");  
    }  
    public static void main(String[] args) {  
        BinTreeTraverse binTree = new BinTreeTraverse();  
        binTree.createBinTree();  
        // nodeList中第0个索引处的值即为根节点  
        Node root = nodeList.get(0);  
  
        System.out.println("先序遍历：");  
        preOrderTraverse(root);  
        System.out.println();  
  
        System.out.println("中序遍历：");  
        inOrderTraverse(root);  
        System.out.println();  
  
        System.out.println("后序遍历：");  
        postOrderTraverse(root);  
    }  
}  

观察代码会发现，先序，中序和后序的代码都差不多，就是三步顺序不一致，大家可以自己试试，区别并不大。

测试题

已知二叉树的前序便利序列为ABCDEF,中序遍历序列为CBAEDF,请问这颗二叉树的后序遍历结果是什么？

需求分析：

首先先绘制这颗树，前序为中左右，所以A为根节点，中序为左中右，所以推测出CB为根节点的左子树，再看前序顺序为BC，所以推测B为A左子树，C为B的左子树。而DEF为A的右子树。根据前中序结合分析，树状图如下：

后序遍历结果：C B E F D A

注意：已知前序遍历序列和中序遍历序列，可唯一确定二叉树。已知后序遍历序列和中序遍历序列，可唯一确定二叉树。已知前序和后序遍历，是不能确定一根二叉树的。

翻转二叉树

解决这个问题，可以获取当前树，将左右结点替换，然后在进入其子结点，用递归思想解决问题：

public static Node reverseTree(Node root) {
		if (root == null) {
			return null;
		} else {
			Node leftNode = reverseTree(root.leftChild); //把左子树翻转
			//把右子树翻转
			Node rightNode = reverseTree(root.rightChild);
			root.leftChild = rightNode;  //把左右子树分别赋给root
			root.rightChild = leftNode;
			return root;
		}
	}

最后分析一下：安卓开发哪些情况下运到的树形结构

在安卓系统中，每个ViewGroup里面又会包含多个或者0个View，每个View或者ViewGroup都有一个整型的id，每次使用ViewGroup的findViewById(int id)的时候，以二叉树查找的方式返回当前ViewGroup下面的View。

源码如下：

public static View find(ViewGroup vg,int id) {
    	if (vg == null) 
    		return null;
    	int size = vg.getChildCount();
    	/** 循环遍历所有孩子*/
    	for (int i = 0; i < size; i++) {
			View v = vg.getChildAt(i);
			/** 如果当前孩子id相同，那么返回，不同而且是ViewGroup就递归*/
			if (v.getId() == id) 
				return v;
			if (v instanceof ViewGroup) {  /** 递归*/
				View temp = find((ViewGroup)v, id);
				if (temp!=null) 
					return temp;
			}
		}
    	/** 到最后都没找到，不包含该id的控件*/
    	return null;
	}

如果编程中有相似功能，也可以使用此思路解决～关于二叉树的知识点总结先到这里，如果之后我再有更深入的认知，会在补充......感谢您的阅读！