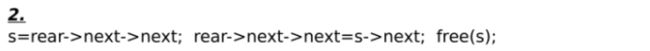数据结构常用常考经典习题【按十大专题总结】
以下都是小旭大一下学期在家上网课的时候,根据教授所出的试题,一份份手写搞成图片粘进word里面的,现在免费做一个小汇总,主要涵盖了一些简单的介绍和10次线下作业及2次思维训练,涵盖了几乎所有的经典习题类型,方便大家借鉴交流~
一、定义: 数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。数据结构往往同高效的检索算法和索引技术有关。
二、研究对象:
1.数据的逻辑结构: 指反映数据元素之间的逻辑关系的数据结构,其中的逻辑关系是指数据元素之间的前后件关系,而与他们在计算机中的存储位置无关。逻辑结构包括: 集合结构(数据结构中的元素之间除了"同属一个集合" 的相互关系外,别无其他关系) 线性结构(数据结构中的元素存在一对一的相互关系) 树形结构(数据结构中的元素存在一对多的相互关系)
图形结构(数据结构中的元素存在多对多的相互关系)2.数据的物理结构: 指数据的逻辑结构在计算机存储空间的存放形式。
数据的物理结构: 数据结构在计算机存储器中的具体实现,是逻辑结构的表示(又称存储映像),它包括数据元素的机内表示和关系的机内表示。由于具体实现的方法有顺序、链接、索引、散列等多种,所以,一种数据结构可表示成一种或多种存储结构。
数据元素的机内表示(映像方法): 用二进制位(bit)的位串表示数据元素。通常称这种位串为节点(node)。当数据元素有若干个数据项组成时,位串中与各数据项对应的子位串称为数据域(data
field)。因此,节点是数据元素的机内表示(或机内映像)。关系的机内表示(映像方法): 数据元素之间的关系的机内表示可以分为顺序映像和非顺序映像,常用两种存储结构:顺序存储结构和链式存储结构。顺序映像借助元素在存储器中的相对位置来表示数据元素之间的逻辑关系;非顺序映像借助指示元素存储位置的指针(pointer)来表示数据元素之间的逻辑关系。
3.数据结构的运算(这里就不一一赘述啦)
第一次线下作业【数据及其结构】
【简单定义、数据的两种存储方式、ADT三元组、二分归并排序的公式推导及复杂度求解】

typedef int Status;
typedef int ElemType;
typedef ElemType *Triplet;
Status InitTriplet(Triplet &T,ElemType v1,ElemType v2,ElemType v3){
T=(ElemType *)malloc(3 *sizeof(ElemType));
if(!T) exit(OVERFLOW);
T[0]=v1;
T[1]=v2;
T[2]=v3;
return OK;
}
第二次线下作业【表】
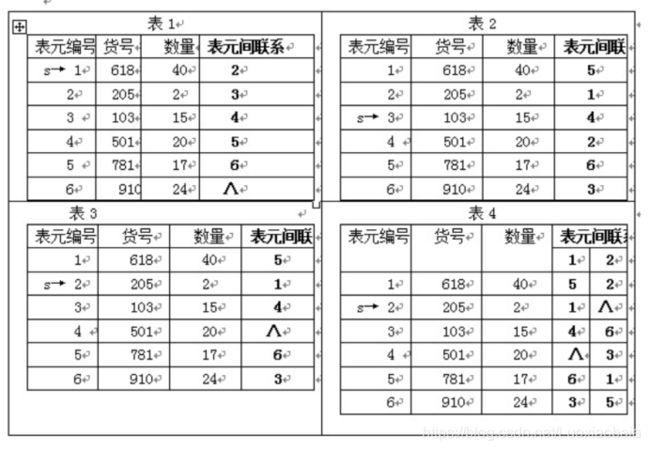
【顺序表的插入删除平均移动元素次数、单循环链表删除节点的操作、各表的存储方式】
第三次线下作业【堆栈】
SqStack *s
(s->top)-(s->base)
s->top
(s->top)++
1
第四次线下作业【队列】
【循环队列的优点及判空满、单循环链表表示链队时头尾指针出入队的操作时间、定义顺序队列的代码补充】
![]()






第五次线下作业【字符串】
第六次线下作业【矩阵&广义表】
【求矩阵的向量copt值、求广义表深度&长度&表头表尾、用head()&tail()函数取出LS中原子的运算命令组合】


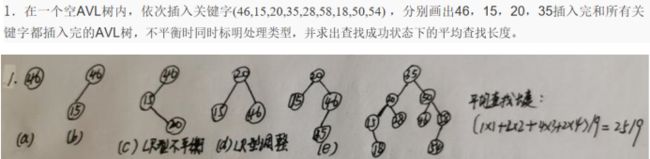
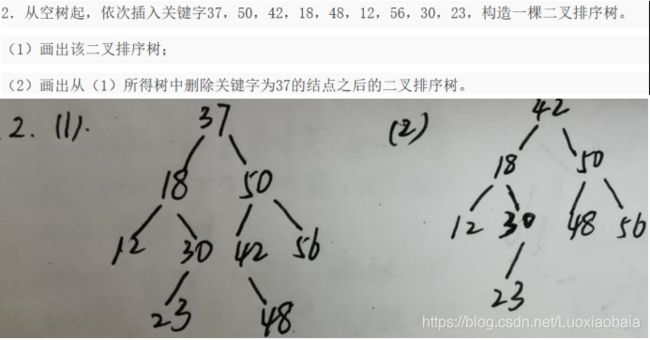
第七次线下作业【树】
第八次线下作业【图】
【连通图、无向图、连通分量、最小生成树(Prim和Krucskal算法)】

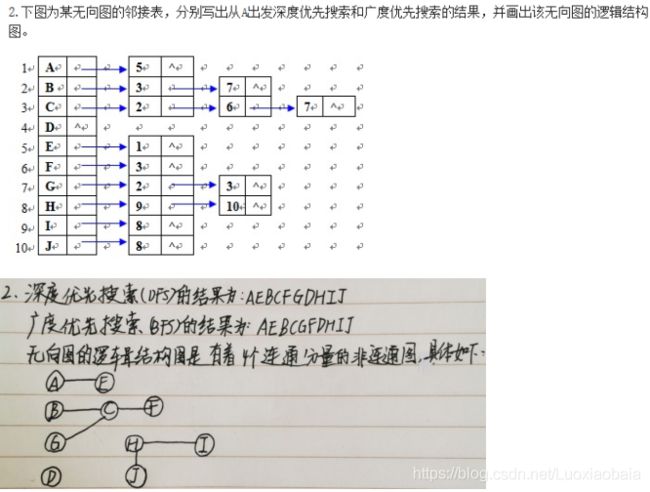

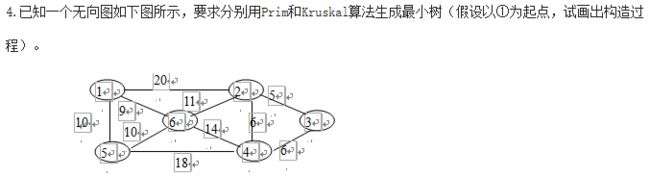



第九次线下作业【散列/哈希】
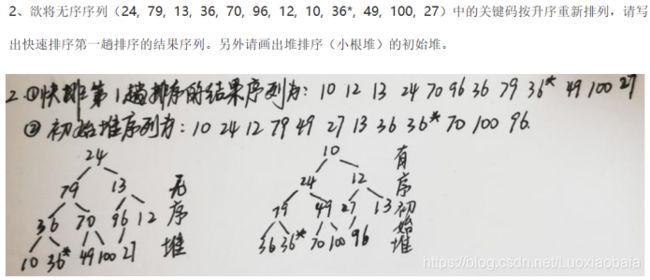
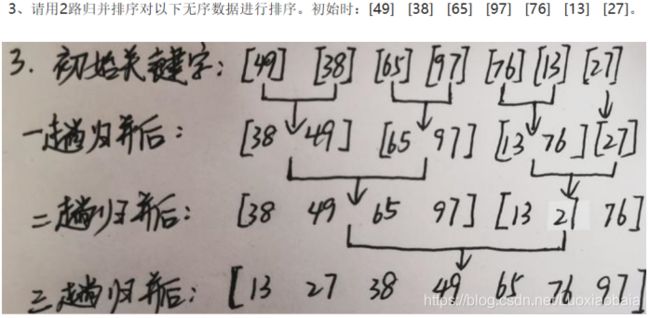
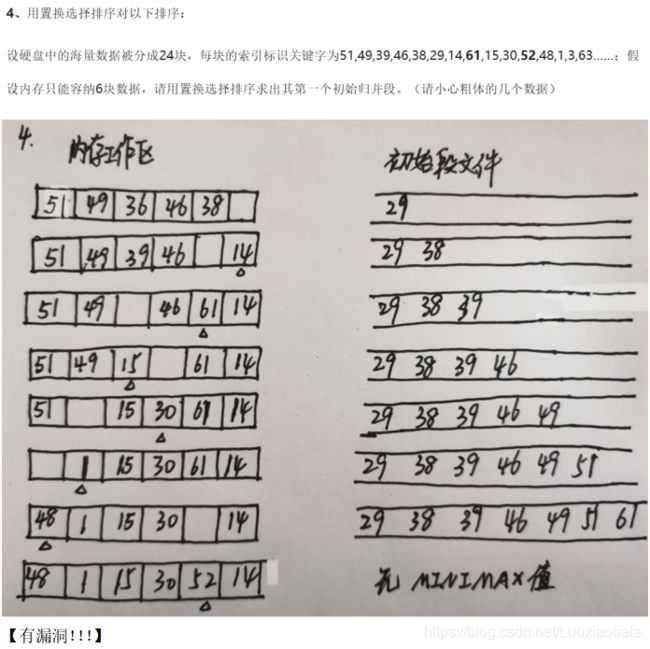
第十次线下作业【排序】
第一次思维训练【合并新闻列表】
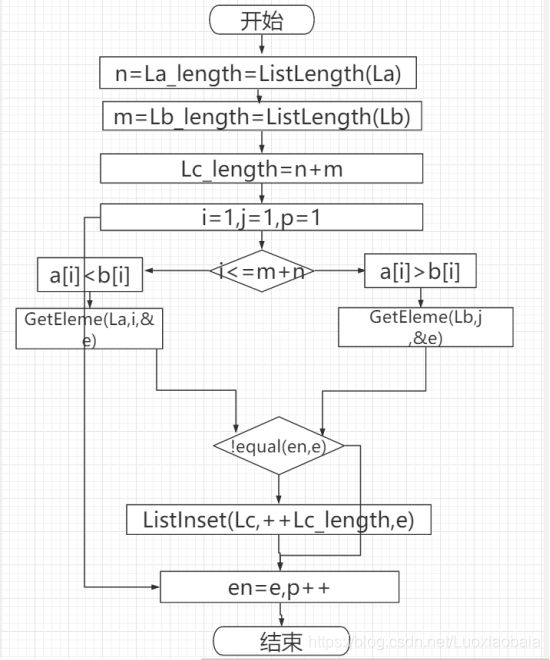
第二次思维训练【合并有序线性表】
#include 运行结果:
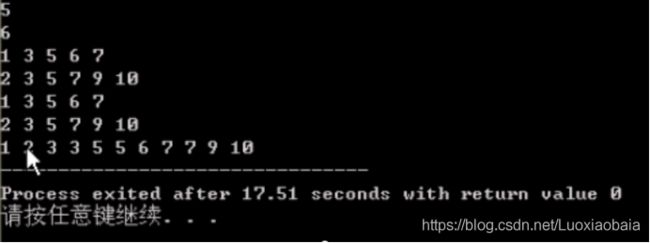
【大家在掌握理论知识之后,可以结合下方链接的文章巩固应用所学的知识,进入实战演练,明确不同篇章的具体要求,在自己的编码能力上更上一个层次 】
手把手教你写数据结构八大实验报告