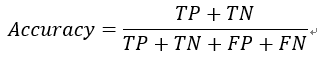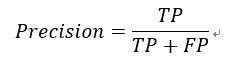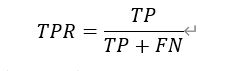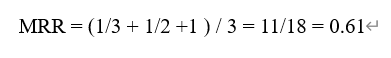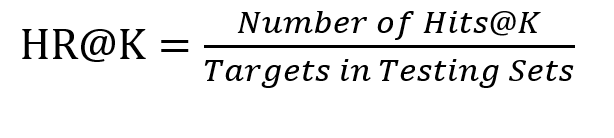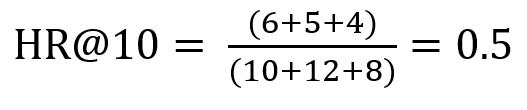【科研分享】推荐算法指标总结(ACC,Precision,Recall,F1,FPR,TPR,ROC,AUC,MAP,MRR,HR,NDCG...)
常用的推荐算法指标解释总结
本文目前包含指标解释包括(Accuracy(ACC),Precision,Recall,F1,FPR,TPR,ROC,AUC,MAP,MRR,HR,NDCG.... )稍后还会继续更新。笔者也是站在巨人的肩膀上学习,希望对大家有所帮助。
1. 指标计算的参数(TP,TN,FP,FN)
TP:被正确分类的正例(True-Positive),即正例被分成正例的样本。
TN:被正确分类的负例(True-Negative),即负例被分成负例的样本。
FP:被错误分类的负例(False-Positive),即本来是负例却被分成了正例的样本。
FN:被错误分类的正例(False-Negative),即本来是正例却被分成了负例的样本。
2. 预测精准度(Accuracy)
即被正确分类的正例和负例,占所有参与分类样本的比例。表达式如下
3. 模型精确率(Precision)
模型预测出的正例,有多少是真实的,即被正确分类的正例占所有被分成的正例的比例。表达式如下:
4. 召回率(Recall)
应该向用户推荐的样本中,有多少被模型所成功召回,即在所有的正例样本中,有多少被模型成功地找出。表达式如下:
5. F1分数(F1)
F1 Score是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了、模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种调和平均,它的最大值是1,最小值是0。表达式如下:
更一般的,还有Fi分数的定义:
其中F2与F0.5也很常用。通过上式不难看出,在F2分数中,召回率的权重高于精确率,而F0.5分数中,精确绿的权重高于召回率。这两种分数分别适用于对精确率和召回率要求不同的应用场景。
6. 假正例率(FPR)
即所有的负例中,被模型分成正例的概率。表达式如下:
7. 真正例率(TPR)
即所有的正例中,被模型分成正例的概率。其表达式与召回率一样:
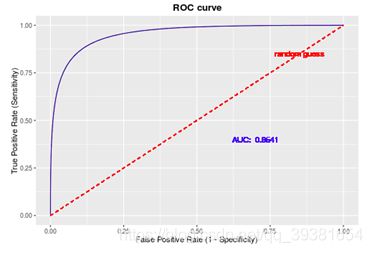
8. 接受者操作特征曲线(ROC)
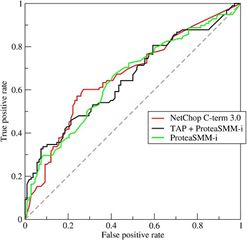
ROC曲线是计算AUC的关键,它的横坐标为FPR,纵坐标为TPR,如下图所示:
ROC曲线能很容易的查出任意阈值对学习器的泛化性能影响,ROC曲线越靠近左上角,模型的准确性就越高。最靠近左上角的ROC曲线上的点是分类错误最少的最好阈值,其假正例和假反例总数最少。如下图所示:
9. AUC(Area Under Curve)
由于ROC曲线不是很好评价到底哪种base-line的分类表现更好,所以才有了去计算ROC曲线下面积(AUC)的操作,作为一个数值显然对应AUC数值更大的分类器效果更好。(由于ROC曲线一般都处于y=x这条直线的上方,所以AUC的取值范围在0.5和1之间)
10. MAP(Mean Average Precision)
此概念不好理解,举个例子,例如对于List 1:【命中,命中,未命中,未命中,未命中】和List 2:【未命中,未命中,未命中,命中,命中】这两个Top - 5的推荐列表,通过计算他们的Precision都是2/5,但是显然第一个推荐模型的性能要高于第二个推荐模型,因为第一个模型在前1、2位就已命中用户的兴趣。
理解过程Precision → Average Precision → Mean Average Precision
Step1:精确率只是考虑了返回推荐结果中Item的个数,没有考虑被推荐Item命中的顺序关系。对一个推荐系统来说返回的结果的顺序关系是很重要的,而且与用户兴趣越相关的Item应该排序越靠前越好,于是出现了AP的概念。
Step2:对一个有序的列表,计算AP的时候要先求出每个位置上的precision,然后对所有的位置的precision再取平均。如果该位置的文档是不相关的则该位置 precision取0.
如下表所示,对于推荐列表【命中,命中,未命中,未命中,未命中】(即假设用户实际购买了3种商品,而我们的推荐系统在前5个只给出了2个)
| ID |
Correctness |
Point |
| 1 |
命中,1 |
1 |
| 2 |
命中,1 |
1 |
| 3 |
未命中,0 |
2/3 |
| 4 |
未命中,0 |
2/4 |
| 5 |
未命中,0 |
2/5 |
它的平均精度应为:(其中,min(3,5)中的3为用户实际购买数3而不是命中数2,5为推荐系统提供的Top-K,K=5)
而如下表所示的列表【未命中,未命中,未命中,命中,命中】:
| ID |
Correctness |
Point |
| 1 |
未命中,0 |
0 |
| 2 |
未命中,0 |
0 |
| 3 |
未命中,0 |
0 |
| 4 |
命中,1 |
1/4 |
| 5 |
命中,1 |
2/5 |
它对应的平均精度则为:
最终计算MAP(Mean Average Precision)时,只需要再为所有用户 u 的AP再取一次均值(mean)就可以了。
11. 平均倒数排名(MRR)
即第一个结果匹配,分数为1,第二个匹配分数为0.5,第n个匹配分数为1/n,如果没有匹配的句子分数为0。最终的分数为所有得分之和。举例来说:
有3个用户分别被推荐了如下图所示的序列,如下图所示:
| 用户实际兴趣 |
推荐序列Top-3 |
命中位置序号 |
匹配分数(倒数) |
| A3 |
A1, A2, A3 |
3 |
1/3 |
| B1 |
B1, B2, B3 |
1 |
1 |
| C2 |
C1, C2, C3 |
2 |
1/2 |
所以它的MRR计算表达式如下:
12. Top-K命中率(HR@K)2021-10-27更新
Top-K命中率,也叫作Hit Ratio@K,在推荐系统评价指标中很常见。通常会以HR@5和HR@10的形式出现在论文中,用于衡量模型召回的list中前5个或前10个items在targets list中的命中率,它的本质和召回率并无差别,但更能够体现模型对于Top-K热门items的推荐性能。其表达式可以抽象为:
其中,分母是所有的测试集中target items的总和,分子表示每个用户top-K列表中命中测试集合的item个数的总和。
在此我引用其他前辈文章(文末给出引用)的一个例子:三个用户在测试集中的商品个数分别是10,12,8,模型得到的top-10推荐列表中,分别有6个,5个,4个在测试集中,那么此时HR的值是:
13. 平均NDCG@K(Normalized Discounted Cummulative Gain)
NDCG也是非常常见的评价指标之一,通常与HR相同,会评价NDCG@5和NDCG@10,想要理解NDCG则需要先了解DCG和CG的概念,此处继续引用前辈的部分博文来做解释。
CG为累积增益:CG表示将每个推荐结果相关性的分值累加后的得分,其表达式可以抽象为:
![]()
其中,rel表示第i个正数位置上推荐结果的相关性,k表示推荐列表的长度。然而,CG没有考虑每个推荐结果处于不同位置对整个推荐结果的影响,例如,我们总是希望相关性大大的结果排在前面,相关性低的排在前面会影响用户体验。在此基础上DCG引入了位置影响因素,计算表达式可以抽象为:
![]()
不难看出,推荐结果list中item与target item所计算出的相关性越大,DCG的得分就越大。同时,相关性越高的item排在推荐列表前面的话,推荐效果越好,DCG的得分也就越大。然而,DCG针对不同的推荐列表之间很难进行横向评估,而我们评估一个推荐系统不可能仅使用一个用户的推荐列表及相应结果进行评估,而是对整个测试集中的用户及其推荐列表结果进行评估。那么,不同用户的推荐列表的评估分数就需要进行归一化,也就是上文所述的NDCG。在此之前还需要引入一个伴生概念IDCG(Ideal DCG),它表示推荐系统某一用户返回的最好推荐结果列表, 即假设返回结果按照相关性排序, 最相关的结果放在最前面, 此序列的DCG为IDCG。即DCG∈(0, IDCG],故NDCG的值介于(0,1],那么我们可以抽象出用户u所对应的NDCG@K定义为:
![]()
但这依然不是论文中常见的NDCG@K,由于一个数据集中包含大量的user,所以需要再修改以下计算公式为:(又称为平均NDCG@K)
![]()
写在最后
本文对于推荐算法的一些实验和论文中常见指标进行了学习性总结,文章中出现的知识是借鉴自多位学者的博文。笔者在原文基础上补充了一些内容来方便大家理解,同时用以学习和自查。本文也将在不断学习过程中进行修正和更新。
原文1链接:https://blog.csdn.net/hackerzer/article/details/79632951
原文2链接:https://blog.csdn.net/weixin_41332009/article/details/113343838
原文3链接:https://blog.csdn.net/m0_45338067/article/details/109010821