PyTorch快速入门
什么是PyTorch?
PyTorch是基于以下两个目的而打造的python科学计算框架:
- 无缝替换
NumPy,并且通过利用GPU的算力来实现神经网络的加速。 - 通过自动微分机制,来让神经网络的实现变得更加容易。
安装
pip install torch
pip install torchvision
张量
什么是张量(Tensor)?
可以将张量通俗的理解为多维数组
| 维数 | 阶 | 名字 | 数学实例 | 示例 |
|---|---|---|---|---|
| 0-D | 0 | 标量(scalar) | 数字(只有大小) | 255 |
| 1-D | 1 | 向量(vector) | 向量(大小和方向) | [1.1, 2.2, 3.3 ] |
| 2-D | 2 | 矩阵(matrix) | 数据表 | [[1.1, 2.2, 3.3 ], [1.1, 2.2, 3.3 ]] |
| 3-D | 3 | 3阶张量 | 工用数据、时间序列数据、股价、文本数据、彩色图片 | [[[1.1, 2.2, 3.3 ], [1.1, 2.2, 3.3 ]]] |
| n-D | n | n阶张量 |
张量初始化
import numpy as np
import torch
直接生成张量
# 用list直接初始化一个张量
data = [[1, 2], [3, 4]]
x_data = torch.tensor(data)
tensor([[1, 2],
[3, 4]])
通过Numpy数组来生成张量
# 通过ndarray初始化张量
np_array = np.array(data)
x_np = torch.from_numpy(np_array)
tensor([[1, 2],
[3, 4]], dtype=torch.int32)
通过已有的张量来生成新的张量
# 继承原有张量生成一个新的全1张量(保留原张量属性)
x_ones = torch.ones_like(x_data)
# 继承原有张量生成一个新的随机张量并重写张量的数据类型
x_rand = torch.rand_like(x_data, dtype=torch.float)
tensor([[0.3694, 0.6384],
[0.0699, 0.2854]])
通过指定数据维度来生成张量
# 指定张量维度
shape = (2, 3,)
# 随机张量
rand_tensor = torch.rand(shape)
# 全1张量
ones_tensor = torch.ones(shape)
# 全0张量
zeros_tensor = torch.zeros(shape)
tensor([[0.7085, 0.1440, 0.6007],
[0.7662, 0.5017, 0.4305]])
tensor([[1., 1., 1.],
[1., 1., 1.]])
tensor([[0., 0., 0.],
[0., 0., 0.]])
张量属性
tensor = torch.rand(3, 4)
print("维度:{}".format(tensor.shape))
print("数据类型:{}".format(tensor.dtype))
print("存储设备:{}".format(tensor.device))
维度:torch.Size([3, 4])
数据类型:torch.float32
存储设备:cpu
张量运算
索引和切片
# 创建一个4*4的全1张量
tensor = torch.ones(4, 4)
# 将第1列(从0开始)的数据全部赋值为0
tensor[:, 1] = 0
tensor([[1., 0., 1., 1.],
[1., 0., 1., 1.],
[1., 0., 1., 1.],
[1., 0., 1., 1.]])
拼接
# 将一组张量按照指定的维度进行拼接
t1 = torch.cat([tensor, tensor, tensor], dim=1)
tensor([[1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
[1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
[1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.],
[1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 1., 1.]])
张量乘积
# 初始化一个张量
a = [[1, 2], [3, 4]]
a_tensor = torch.tensor(a)
# 求张量乘积(法一)
b_tensor = a_tensor.mul(a_tensor)
# 求张量乘积(法二)
b_tensor = a_tensor * a_tensor
tensor([[ 1, 4],
[ 9, 16]])
矩阵乘法
# 初始化向量
c = [[1, 2, 3], [4, 5, 6]]
d = [[1, 2], [3, 4], [5, 6]]
c_tensor = torch.tensor(c)
d_tensor = torch.tensor(d)
# 向量乘法(法一)
e_tensor = c_tensor.matmul(d_tensor)
# 向量乘法(法二)
e_tensor = c_tensor @ d_tensor
tensor([[22, 28],
[49, 64]])
自动赋值运算
# 初始化一个3*3的全1向量
f_tensor = torch.ones((3, 3,))
# 对该向量进行自动赋值运算
f_tensor.add_(2)
tensor([[3., 3., 3.],
[3., 3., 3.],
[3., 3., 3.]])
神经元与神经网络
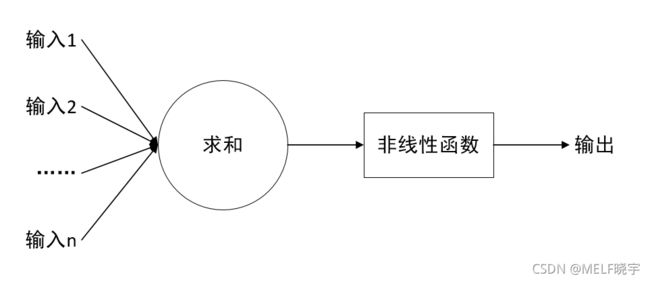
神经元(MP模型)
在不考虑非线性函数时,其数学表达式为:
y = x ∗ W + b y = x * W + b y=x∗W+b
其中程序执行 x ∗ w + b x*w+b x∗w+b的过程称为前向传播
若输入 x x x有 n n n个,输出 y y y有 m m m个,则:
x = [ x 0 x 1 ⋮ x n ] , W = [ w 00 ⋮ w 0 m w 10 ⋮ w 1 m ⋮ ⋮ ⋮ x n 0 ⋮ w n m ] , b = [ b 0 b 1 ⋮ b m ] , y = [ y 0 y 1 ⋮ y m ] x =\begin{bmatrix} x_0 \\ x_1 \\ \vdots \\ x_n \\ \end{bmatrix}, W = \begin{bmatrix} w_{00}& \vdots &w_{0m} \\ w_{10}& \vdots &w_{1m} \\ \vdots& \vdots &\vdots \\ x_{n0}& \vdots &w_{nm} \\ \end{bmatrix}, b =\begin{bmatrix} b_0 \\ b_1 \\ \vdots \\ b_m \\ \end{bmatrix}, y =\begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_m \\ \end{bmatrix} \\ x=⎣⎢⎢⎢⎡x0x1⋮xn⎦⎥⎥⎥⎤,W=⎣⎢⎢⎢⎢⎢⎢⎡w00w10⋮xn0⋮⋮⋮⋮w0mw1m⋮wnm⎦⎥⎥⎥⎥⎥⎥⎤,b=⎣⎢⎢⎢⎡b0b1⋮bm⎦⎥⎥⎥⎤,y=⎣⎢⎢⎢⎡y0y1⋮ym⎦⎥⎥⎥⎤
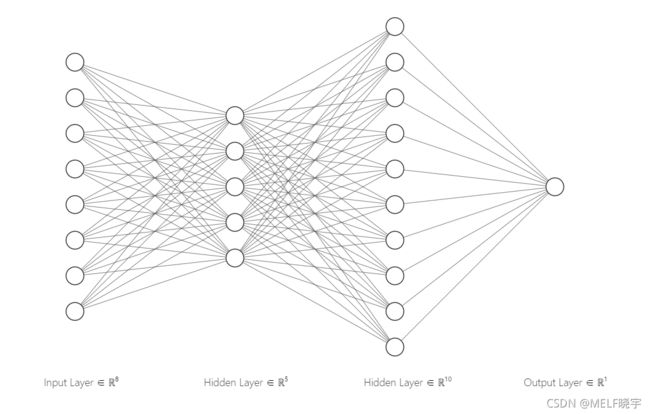
神经网络
人工神经网络,简称神经网络(NN)是在某些输入数据上执行的嵌套函数的集合,每个神经网络由若干个神经元组成。
每个神经网络由 1 1 1个输入层, 1 1 1个输出层以及若干个隐藏层构成。
激活函数
激活函数决定哪些信息保留以传递给后面的神经元
必要性质
- 非线性
- 连续可微性
- 单调
- 近似恒等
常见激活函数
Sigmoid
f ( x ) = δ ( x ) = 1 1 + e − x f(x)=\delta(x) = \frac{1}{1+e^{-x}} f(x)=δ(x)=1+e−x1
Tanh
f ( x ) = t a n h ( x ) = s i n h ( x ) c o s h ( x ) = e x − e − x e x + e − x = 2 δ ( 2 x ) − 1 f(x) = tanh(x)=\frac{sinh(x)}{cosh(x)}=\frac{e^x-e^{-x}}{e^x +e^{-x}} =2\delta(2x)-1 f(x)=tanh(x)=cosh(x)sinh(x)=ex+e−xex−e−x=2δ(2x)−1
Hard Tanh
f ( x ) = { + 1 , x > 1 x , 其 他 − 1 x < − 1 f(x)= \begin{cases} +1, & x>1 \\ x, & \text 其他\\-1 &x<-1 \end{cases} f(x)=⎩⎪⎨⎪⎧+1,x,−1x>1其他x<−1
ReLU
f ( x ) = m a x ( x , 0 ) f(x) = max(x,0) f(x)=max(x,0)
Softmax
f i ( x ) = e x i ∑ j e x j f_i(x) = \frac{e^{x_i}}{\sum_je^{x_j}} fi(x)=∑jexjexi
LogSoftmax
f i ( x ) = l o g ( e x i ∑ j e x j ) f_i(x)=log(\frac{e^{x_i}}{\sum_je^{x_j}}) fi(x)=log(∑jexjexi)
损失函数
损失函数指的是预测值( y y y)与标准答案( y _ y\_ y_)的差距。
损失函数可以定量的判断 W W W和 b b b的优劣,当损失函数输出最小时,参数 W W W和 b b b会出现最优值。
回归问题
均方误差
M E S ( y , y _ ) = ∑ k = 0 n ( y − y _ ) 2 n MES(y,y\_)=\frac{\sum^{n}_{k=0}(y-y\_)^2}{n} MES(y,y_)=n∑k=0n(y−y_)2
分类问题
二分类问题
铰链损失
多分类问题
训练神经网络
训练 NN 分为两个步骤:
前向传播
在前向传播中,NN对正确的输出进行最佳猜测。 它通过其每个函数运行输入数据以进行猜测。
前向传播的方程为:
h ( x ) w , b = y ~ h(x)_{w,b} = \tilde{y} h(x)w,b=y~
表示在 w , b w,b w,b条件下对于输入 x x x神经网络的输出为 y ~ \tilde{y} y~。
反向传播
在反向传播中,NN根据其猜测中的误差调整其参数。 它通过从输出向后遍历,收集有关函数参数(梯度)的误差导数并使用梯度下降来优化参数来实现。
未完待续……
参考资料
PyTorch官网:https://pytorch.org/
PyTorch中文文档:https://pytorch.apachecn.org/
【tensorflow】浅谈什么是张量tensor:https://blog.csdn.net/qq_31821675/article/details/79188449
人工智能实践:Tensorflow笔记_中国大学MOOC(慕课):https://www.icourse163.org/learn/PKU-1002536002?tid=1462067447#/learn/content?type=detail&id=1238898223&sm=1
双曲正切_百度百科:https://baike.baidu.com/item/%E5%8F%8C%E6%9B%B2%E6%AD%A3%E5%88%87/3194837?fromtitle=tanh&fromid=19711736&fr=aladdin
《PyTorch机器学习从入门到实战》