Python机器学习（三）：K近邻算法(K-Nearest Neighbor-KNN)

Python机器学习（三）：K近邻算法(K-Nearest Neighbor-KNN)

---

一、KNN简介

经验告诉我们，相似的事物经常属于同一个类别，如：头发长度更接近，而影响因子低的通常是一般论文，因此，KNN算法基于属性的相似度，来度量事物属于哪一类

KNN是一种比较成熟也是最简单的机器学习算法，可以用于分类与回归

---

二、度量相似度

1. 欧氏距离(Euclidean Distance)

欧氏距离是KNN算法中最常用的相似度度量方法

1.1 连续属性欧氏距离

根据事物 $A(x_i)$ 的属性 $(x_1,x_2)$ 和事物 $B(y_i)$ 的属性 $(y_1,y_2)$来分析事物的相似性：
$$d(x,y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2}$$

$d(x,y)$ 实际上就是二维平面中两个点之间的距离（在二维和三维空间中，欧氏距离实际上就是两点之间的距离）：

推广到 $n$ 维（即 $n$ 个属性）的欧氏距离：
$$d_E(x,y)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

其中，$x_i$ 表示事物 $A$ 的属性，$y_i$ 表示事物 $B$ 的属性，$i$ 表示第 $i$ 个属性

1.2 连续属性欧氏距离的属性尺度

在计算连续属性的欧氏距离时，必须考虑属性值的尺度，如：在式 $d(x,y)=\sqrt{(1-0{)}^2+(0.2-0.1{)}^2+(296-107{)}^2}$ 中，根号里三项的结果分别为：$1、0.01、35721$，显然在这个式子中，第三项完全控制了计算结果，而其他两项对距离的贡献极低，这很不合理

归一化： 我们可以将多个处于不同区间的连续属性，归一化到 $[0,1]$ 内，这样每个属性对欧氏距离的贡献都一样了
$$x_{修正}=\frac{x-min}{max-min}$$

其中，$x$ 为该属性的原取值，$x_{修正}$ 为该属性的最终取值，$max$ 和 $min$ 分别表示该属性的最大值和最小值，容易证明，$x_{修正}$ 落在 $[0,1]$ 间

标准化： 不将值绑定到特定的范围内，受异常值的影响更小
$$x_{修正}=\frac{x-E(x)}{D(x)}$$

其中，$E(x)$ 是该属性的均值，$D(x)$ 是该属性的方差

1.3 离散属性欧氏距离

对于离散属性欧氏距离，有如下表达式：
$$d_M(x,y)=\sqrt{\sum _{i=1}^{n}d(x_i,y_i)}$$

$$最简单的情况时：d(x_i,y_i)=\{\begin{array}{rl}0& ，x_i=y_i\\ 1& ，x_i\ne y_i\end{array}$$

$x_i=y_i$ ，表示属性值相同，因此距离为 $0$；$x_i\ne y_i$，表示属性值不同，因此距离为 $1$

1.4 离散属性间的距离的误导

我们不能机械性地运用上式而无视了给定域的特殊性，如：当我们以季节为属性时
①夏季和冬季是不同的，因此 $d(Summer,Winter)=1$
②夏季与秋季是不同的，因此 $d(Summer,Autumn)=1$
然而，通常我们认为，夏季与冬季的差异比夏季与秋季的差异更大，因此 $d(Summer,Winter)$ 和 $d(Summer,Autumn)$ 的值不应该都等于1，而应该考虑加入更多的中间值（可以考虑取多个小数，使其归一化）

2. 曼哈顿距离(Manhattan distance)

想象你在城市道路里，要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个曼哈顿距离，曼哈顿距离实际上就是两点间的垂直距离

曼哈顿距离的表示式如下：
$$d_E(x,y)=\sqrt{\sum _i|x_i-y_i|}$$

3.切比雪夫距离(Chebyshev distance)

切比雪夫距离表示式如下：
$$d(x,y)=ma{x}_i|x_i-y_i|$$

切比雪夫距离采取了所有属性中的最大距离

4.闵可夫斯基距离(Minkowski distance)

闵可夫斯基距离表示式如下：
$$d(x,y)=(\sum _i|x_i-y_i|{)}^{\frac{1}{p}}$$

其中，$p=1$ 时为曼哈顿距离，$p=2$ 时为欧氏距离，当 $p\to \infty$ 取极限时，可以得到切比雪夫距离

5.其他距离

汉明距离(Hamming distance)、余弦相似度…

---

三、KNN算法流程

在上一章中，我们知道了如何通过计算事物的属性之间的距离，来度量事物的相似度

KNN主要思想：

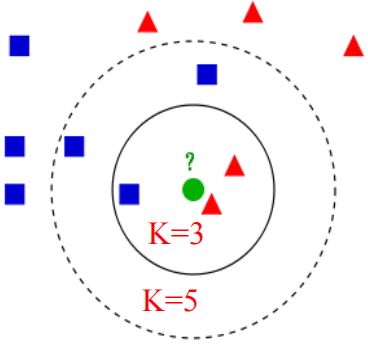
在KNN算法中，如果一个样本在特征空间中与 $k$ 个实例最为相似（即特征空间中最邻近或距离最小），那么这 $k$ 个最近邻的实例中，大多数实例属于哪个类别，则该样本也属于这个类别

而KNN中的K，指的就是上述中的 $k$

对于分类问题：对新的样本，根据其 $k$ 个最近邻的训练样本的类别，通过多数表决等方式进行预测
对于回归问题：对新的样本，根据其 $k$ 个最近邻的训练样本标签值的均值作为预测值

算法流程：

1. 计算测试对象到训练集中每个对象的距离
2. 按照距离的远近排序
3. 选取与当前测试对象距离最近的 $k$ 个训练样本，作为该测试对象的 $k$ 个最近邻
4. 统计这 $k$ 个邻居的标签
5. $k$ 个邻居里频次最高的标签，即为测试对象的标签

对于如果确定 $k$ 的取值：

1. 当 $k=1$ 时，只有一个最近邻，如果训练集的噪声较多时，它容易受到噪声的干扰
2. 当 $k>1$ 时，能够更好地抵抗噪声
3. 当 $k\in \{偶数\}$ 时，在二分类问题中可能会出现【最近邻样本分别属于两类标签的数量是相等的，无法完成决策】的情况，因此在二分类问题中，$k$ 通常取奇数
4. 当 $k$ 的取值越小，越容易过拟合；当 $k$ 的取值越大，越容易欠拟合

KNN的优缺点：

• 优点：
  1.简单易理解，容易解释
  2.基于实例的学习（消极学习），即没有训练过程
• 缺点：
  1.K较小时对噪声非常敏感
  2.训练集很大时，对内存要求极高
  3.测试过程包含大量根号运算，运算速度慢
  4.KNN在稀疏数据集上的效果并不好

---

四、KNN算法的优化

1.KD树(KD-Tree)

显然，KNN可能需要大量的内存或空间来存储所有数据，并且使用距离或接近程度的度量方法可能会在维度非常高的情况下（有许多输入变量）崩溃，这可能会对算法在解决问题的性能上产生负面影响，这就是所谓的维数灾难

既然KNN的运算量这么大，我们有没有办法可以简化运算量呢？

KD树可以减少KNN计算距离的次数，可以很快地找到与测试点最近邻的K个样本，无需单独计算测试点和训练集中每一个样本之间的距离
KD树是二叉树的一种，是对多维空间的分割方法，KD树可不断地利用垂直于坐标轴的超平面将多维空间切分，形成多维超矩形区域，KD树的每一个结点对应于一个多维超矩形区域

1.1 KD树划分

假设现有 6 个二维数据点集合：$D=\{(2,3),(5,7),(9,6),(4,5),(6,4),(7,2)\}$，其中 $(x,y)$ 分别是两不同属性

首先按属性 $x$ 按顺序排列：$points=\{(2,3),(4,5),(5,7),(6,4),(7,2),(9,6)\}$，得到中位数 $6$（注：由于算法需要以点作为切分，因此这里中位数的计算方法为：$len(points)//2=3，points[3]=6$，简单来说就是取较大的值作为中位数）

根据中位数 $x=6$，将点集按 $x$ 切分为 $\{x|x<6\}$ 和 $\{x|x>6\}$ 两个点集，其中 $\{(2,3),(4,5),(5,7)\}$ 在左子树，$\{(7,2),(6,9)\}$ 在右子树

此时，由属性 $x=6$ 作为切分边界就可以将二维平面 $(x,y)$ 切分开来，如果是在三维空间 $(x,y,z)$ 中，切分边界就是一个平面，将三维空间切分为立方体，如果是在 $N>3$ 的高维空间中，则切分边界就是一个超平面，将高维空间切分。其中节点 $(6,4)$ 视为切分边界，将空间划分开，这也是为什么中位数需要取具体点的原因

然后，二叉树的左右子树分别按属性 $y$ 分别求出各点集的中位数为 $y=5$ 和 $y=6$ ，因此可以继续对点集进行切分，如图。其中节点 $(4,5)$ 和 $(9,6)$ 视为切分边界

被继续划分出来的空间如图所示，现在被已划分为四个平面（在高维空间中，将由超平面划分为多个超空间）：

继续切分，所有属性按顺序循环取中位数对空间进行切分，直到最后子树的点集只剩下一个点，则叶子节点最后以自己作为最后的切分

最后切分出的多个空间如图所示：

这样，一棵KD树就构建好了，其中被划分为 $7$ 个空间

1.2 KD树搜索

KD树构建好以后，就可以利用KD树来进行K近邻搜索了

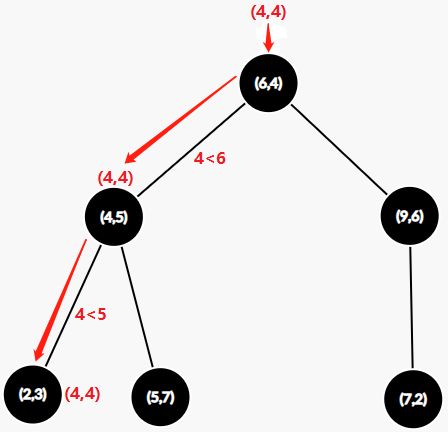
（一）假设我们现在要寻找点 $P(4,4)$ 的K个最近邻，首先我们向KD树输入点 $P(4,4)$，按照KD树的切分，我们很快可以将点 $P$ 归到 $(2,3)$ 叶子节点上，此时，我们暂时认为 $(2,3)$ 是点 $P$ 的K个最近邻之一，放入最近邻容器中，最近邻容器可容纳K个点

（二）此时，我们从叶子节点 $(2,3)$ 开始往上回溯，在父节点 $(4,5)$ 上，先判断最近邻容器是否已满K个点，若未满，则将点 $(4,5)$ 加入最近邻容器中；若已满，则比较点 $(4,5)$ 到点 $P$ 的距离和最近邻容器中距离点 $P$ 最远的那个点的距离的大小，若点 $(4,5)$ 更近，则替换最近邻容器中那更远的点

计算点 $P$ 到父节点 $(4,5)$ 的切分界面的距离：
①若该距离大于最近邻容器中距离点 $P$ 最远的那个点的距离，则说明右子树上不存在比最近邻容器中的点更近邻的点，如果最近邻容器已满，则无需访问右子树；
②若该距离小于最近邻容器中距离点 $P$ 最远的那个点的距离，则说明右子树上可能存在更近邻的点，需要向下访问右子树。访问右子树时，如果右子树的深度大于 $1$，同样需要根据切分界面将点 $P(4,4)$ 分配到某一叶子节点，再参考上述过程进行回溯

（三）访问完右子树后，从 $(4,5)$ 继续向上回溯，在父节点 $(6,4)$ 上，先判断最近邻容器是否已满K个点，若未满，则将点 $(6,4)$ 加入最近邻容器中；若已满，则比较点 $(6,4)$ 到点 $P$ 的距离和最近邻容器中距离点 $P$ 最远的那个点的距离的大小，若点 $(6,4)$ 更近，则替换最近邻容器中那更远的点

计算点 $P$ 到父节点 $(6,4)$ 的切分界面的距离：
①若该距离大于最近邻容器中距离点 $P$ 最远的那个点的距离，则说明右子树上不存在比最近邻容器中的点更近邻的点，如果最近邻容器已满，则无需访问右子树；
②若该距离小于最近邻容器中距离点 $P$ 最远的那个点的距离，则说明右子树上可能存在更近邻的点，需要向下访问右子树。访问右子树时，如果右子树的深度大于 $1$，同样需要根据切分界面将点 $P(4,4)$ 分配到某一叶子节点，再依照上述（二）、(三）的过程进行回溯

（四）仿照步骤（二）、(三），直到访问到根节点为止，结束，将最近邻容器中的点按距离进行排序…

KD树在20维属性以内的效果最佳，在超过20维后的效率表现并不好

2.Ball-Tree

为了改进KD树沿着笛卡尔坐标进行划分的低效率，Ball-Tree将在一系列嵌套的超球体上分割数据，Ball-Tree使用超球面而不是超矩形划分区域，虽然在构建数据结构上的花费大于KD树，但Ball-Tree在高维数据上都表现出更高的效率

KD树在搜索路径优化时使用的是两点之间的距离来判断，而Ball树则是比较两超球体半径之和与球心到测试点的距离大小判断超球体内是否存在最近邻的点

---

五、KNN的sklearn实现

1.sklearn中的KNN

from sklearn.neighbors import KNeighborsClassifier

knn = KNeighborsClassifier(n_neighbors, weights…)

初始化KNN分类器

n_neighbors int，default=5，KNN的近邻数，即K值
weights 各近邻的权重，{‘uniform’：各权重相等, ‘distance’：根据距离赋予权重，权重与距离成反比} or callable：用户自定的权重计算函数，default=’uniform’
algorithm 搜索近邻的算法，{‘auto’：尝试根据fit方法来决定最优算法, ‘ball_tree’：使用ball-tree, ‘kd_tree’：使用KD树, ‘brute’：使用暴力搜索}, default=’auto’，一般在属性维度小于 $20$ 时使用KD树，大于 $20$ 时使用Ball树
leaf_size int，default=30，决定构建KD树和ball树的大小，这个值会影响树的构建速度和搜索速度，也影响存储树所需的内存大小
p 即闵可夫斯基距离中的p值，p=1：曼哈顿距离，p=2：欧氏距离，当p→$\infty$取极限：切比雪夫距离，int，default=2
n_jobs {int, None}，default=None，并行处理设置，临近点搜索并行工作数；若为-1，则CPU的所有 cores 都用于并行工作
注：关于KNN，如果发现两个邻居，邻居k+1和k具有相同距离但不同标签，则结果将取决于训练数据的排序

2.使用KNN进行手写数字识别

2.1 熟悉sklearn手写数字数据集

from sklearn.datasets import load_digits

# 下载手写识别数据集
digits = load_digits()
digits_X, digits_y = digits["data"], digits["target"]

import pandas as pd
print(pd.array(digits_y).unique())

发现手写数字数据集的标签就是 $0～9$ 的数字

数据集中，digits.images[0]$～$digits.images[9] 表示第一组 $0～9$ 数据集，digits.images[10]$～$digits.images[19] 表示第二组 $0～9$ 数据集…

# 显示数字0的数据形式 
print(digits.images[0], digits.images[0].shape)
# 数字0的图片
plt.imshow(digits.images[0])

发现手写数字的图像是一个 $8\times 8$ 的列表，其中值越小，代表颜色越深，值越大，代表颜色越浅，以此组成二维图像， 而这个 $8\times 8=64$ 个数值就是数据集的特征/属性

print(digits_X.shape, digits_y.shape)

再看一下数据的维度，我们就大致了解了手写数字数据集，其中包含了 $1797$ 个数字和它们的标签，$64$ 表示 $8\times 8$ 列表数据

2.2 构建KNN分类器

%matplotlib inline
import matplotlib.pyplot as plt

# 下载手写数字数据集
from sklearn.datasets import load_digits
digits = load_digits()
# 获取样本数据和标签
digits_X, digits_y = digits["data"], digits["target"]

# 划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(digits_X, digits_y, random_state = 66)

# 初始化KNN分类器
from sklearn.neighbors import KNeighborsClassifier
# 由于数据维度较高，最近邻搜索算法使用Ball树搜索
knn = KNeighborsClassifier(n_neighbors=3, weights='distance', algorithm='ball_tree')

# 建立网格搜索
from sklearn.model_selection import GridSearchCV
parameters = {
     "weights": ["uniform", "distance"],
              "n_neighbors": [*range(1, 11)]}
GS = GridSearchCV(knn, parameters, cv=10)
GS.fit(X_train, y_train)
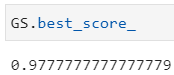
GS.best_params_

网格搜索结果如下，其中 n_neighbors=3, weights='uniform' 最佳


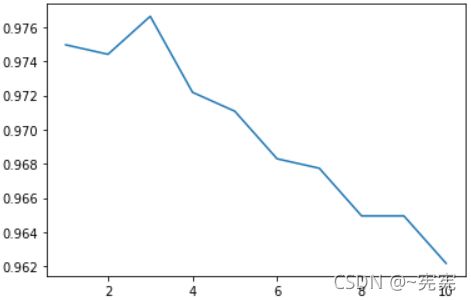
进行10倍交叉验证，用测试集验证一下模型：

from sklearn.model_selection import cross_val_score

scores = []
for i in range(10):
	knn = KNeighborsClassifier(n_neighbors=i+1, weights='uniform', algorithm='ball_tree')
	score = cross_val_score(knn, digits_X, digits_y, cv=10).mean()  # 10倍交叉验证平均值
	scores.append(score)

plt.plot(range(10) + 1, scores)

---

参考资料：
[1]机器学习导论
[2]机器学习-第六章-KNN算法，黄海广