KNN算法的距离公式

理论

1 欧式距离
欧氏距离（L2范数）是最易于理解的一种距离计算方法，源自欧氏空间中两点间的距离公式.
欧式空间是一个非常专业的名词，对于我们编程来说，就等价理解成N维空间即可。

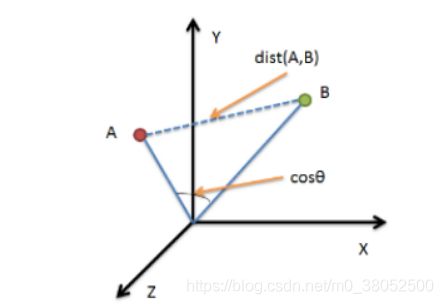
特别要指出的是，一般的，我们可以将N维中的一个测试点与多个样本点间的计算从循环N次计算，转化为一次性计算，见下面的例子。

import numpy as np 
vector1 = np.mat([1,2,3])
vector2 = np.mat([4,5,6])
distance = np.sqrt((vector1-vector2)*((vector1-vector2).T))
print(distance)
##############################
[[5.19615242]]

# 如果想要计算多维空间中，某个点与其他多个点之间的距离，实现快速计算
vector1 = np.array([1,2,3])

vector2 = np.array([[4,5,6],
                   [7,8,9],
                   [10,11,12]])

diffMat = np.tile(vector1, (vector2.shape[0], 1)) - vector2
sqDiffMat = diffMat ** 2
sqDistances = sqDiffMat.sum(axis=1)
o_distances = sqDistances ** 0.5
print(o_distances)
#########################################
[ 5.19615242 10.39230485 15.58845727]

2 杰卡德距离
与杰卡德距离相应的一个词叫做杰卡德相似系数，常用于衡量样本的相似度。
从这一点上看来，比较适合用来做图片识别的工作，但是具体效果如何，还要实际运用实验。

假设，样本A与样本B是两个n维向量，而且所有维度的取值都是0或1。例如：A(0111)和B(1011)。我们将样本看成是一个集合，1表示集合包含该元素，0表示集合不包含该元素。

P：样本A与B都是1的维度的个数

q：样本A是1，样本B是0的维度的个数

r：样本A是0，样本B是1的维度的个数

s：样本A与B都是0的维度的个数

那么样本A与B的杰卡德相似系数可以表示为：

这里p+q+r可理解为A与B的并集的元素个数，而p是A与B的交集的元素个数。
而样本A与B的杰卡德距离表示为：

$$J=\frac{p}{p+q+r}$$

import scipy.spatial.distance as dist  # 导入scipy距离公式
matV = np.array([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
print("dist.jaccard:", dist.pdist(matV,'jaccard'))
#############################################
dist.jaccard: [0.75]

3 汉明距离

两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。

从它计算的数据形式上看，汉明距离也可以用于二值处理后的图像。

matV = np.array([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
smstr = np.nonzero(matV[0]-matV[1]);
len(smstr[0])
####################################
6

4 曼哈顿距离(City Block distance)
从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，驾驶距离是两点间的直线距离吗？显然不是，除非你能穿越大楼。实际驾驶距离就是这个“曼哈顿距离”(L1范数)。而这也是曼哈顿距离名称的来源，曼哈顿距离也称为城市街区距离

vector1 = np.mat([1,2,3])
vector2 = np.mat([4,5,6])
print(sum(abs(vector1-vector2)))
########################################33
[[3 3 3]]

5 切比雪夫距离
国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的任意一个（如图1.11）。那么国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？自己走走试试。你会发现最少步数总是max(| x2-x1| , |y2-y1| ) 步。有一种类似的一种距离度量方法叫切比雪夫距离(L∞范数)。

如果下一个落脚点在起始点的水平位置，那么最少步数是横坐标的差值的绝对值；
如果在垂直位置，那么最少步数是纵坐标的差值的绝对值。
如果是非水平非垂直位置，大家自己试一试。试过之后会发现，还是差不过横坐标差值的绝对值，或者是纵坐标差值的绝对值。

vector1 = np.array([1,2,3])
vector2 = np.array([4,7,5])
print(abs(vector1-vector2).max())
################################

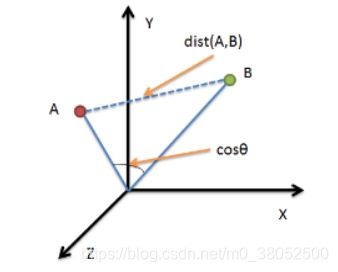
6 余弦距离

几何中夹角余弦可用来衡量两个向量方向的差异，机器学习中借用这一概念来衡量样本向量之间的差异.

vector1 = np.array([1,2,3])
vector2 = np.array([4,7,5])
print(vector1,vector2)
cosV12 = np.dot(vector1,vector2)/(np.linalg.norm(vector1)*np.linalg.norm(vector2))
print(cosV12)
########################################
[1 2 3] [4 7 5]
0.9296696802013682

试验结果

1 欧式距离
准确率:0.9451
F1-Score:0.9718
用时： 2.78871

2 曼哈顿距离
准确率:0.7238
F1-Score:0.8398
用时： 3.12456

3 3切比雪夫距离
准确率:0.1281
F1-Score:0.2271
用时： 2.77712

4 余弦距离
准确率:0.0715
F1-Score:0.1335
用时： 20.69178

5 杰卡德
准确率:0.0998
F1-Score:0.1815
用时： 30.39309
6 汉明距离
准确率:0.9451
F1-Score:0.9718
用时： 1150.58714

可以看出，欧式距离、汉明距离、曼哈顿距离的实验效果都不错，其他的相对来说，比较差劲。另外，六种方法中最费时间的就是汉明距离。

小问题

1 np.tile
np.tile(a, (b,c)) 的介绍

tile有平铺的意思。
在numpy中，np.tile（a,(2)）函数的作用就是将函数将函数沿着X轴扩大两倍。如果扩大倍数只有一个，默认为X轴。
np.tile(a,(2,1))第一个参数为Y轴扩大倍数，第二个为X轴扩大倍数

np.tile(vector1, (vector2.shape[0], 1))
#######################################
array([[1, 2, 3],
       [1, 2, 3],
       [1, 2, 3]])

参考文章

2 numpy中的nonzero

nonzero函数是numpy中用于得到数组array中非零元素的位置（数组索引）的函数。它的返回值是一个长度为a.ndim(数组a的轴数)的元组，元组的每个元素都是一个整数数组，其值为非零元素的下标在对应轴上的值。

matV = np.array([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]])
smstr = np.nonzero(matV[0]-matV[1]);
print(smstr)
len(smstr[0])
##############################################
(array([0, 2, 3, 5, 6, 7]),)
6

参考文章

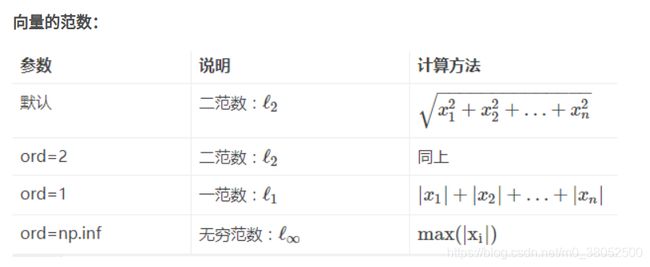
3 np.linalg.norm(求范数)
x_norm=np.linalg.norm(x, ord=None, axis=None, keepdims=False)

参考文章