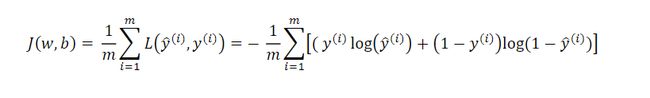Pytorch学习笔记

PyTorch入门

为什么使用PyTorch

PyTorch 是 PyTorch 在 Python 上的衍生. 因为 PyTorch 是一个使用 PyTorch 语言的神经网络库, Torch 很好用, 但是 Lua 又不是特别流行, 所有开发团队将 Lua 的 Torch 移植到了更流行的语言 Python 上.

• 与Tensorflow不同的是：
  • Tensorflow先搭建静态流程图然后代入数据进行计算；
  • PyTorch边代入数据边构建图；

---

二分分类

In a binary classification problem,the result is a discrete value output.

Example：Cat vs Non-Cat

训练目标是训练一个分类器，其输入是由特征向量x表示的图像，并预测相应的标签y是1(这是猫的图像)还是0(这不是猫的图像)。

图像存储在计算机中的三个单独的矩阵中，对应于图像三个矩阵的大小与图像的大小相同，例如，猫的图像的分辨率为 64px * 64px，三个矩阵（RGB）分别为64px * 64px。

单元格中的值表示像素强度，机器学习中，特征向量表示一个对象，在这种情况下，是猫还是没有猫。若要创建特征向量x，像素强度值将分别表示为“unrol”或“reforme”，输入特征向量的维数 x :

nx = 64 * 64 * 3 = 12288

---

Logistic回归

Logistic回归是一种用于有监督学习二分分类问题的学习算法。logistic回归的目标是使预测值与训练数据之间的误差最小化。

Example：Cat vs Non-Cat

给定一个由特征向量x表示的图像，该算法将评估猫在该图像中的概率。

给定 x, 当 0=

Logistic回归中使用的参数有：

• 输入特征向量：

x \in R^nx           

• 训练特征标签：

y = 1|0 

• 权重：

w \in R^nx 

• 阈值：

b \in R

• 输出:

y = \sigma(W^Tx+b)

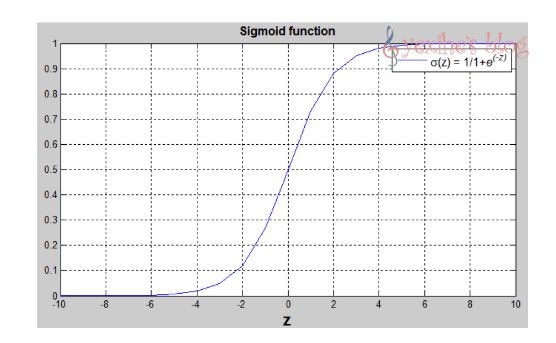
• Sigmoid函数：

s = \sigma(W^Tx+b)=\sigma(z)=1/(1+e^{-z})

---

logistic 回归函数

为了训练出 w 和 b ，我们需要定义函数的成本。
由上面内容可知：

y' = \sigma(W^Tx+b)=\sigma(z)=1/(1+e^{-z})

对于 y’ ，我们想要

y' \approx y

损失函数
损失函数测量预测值 y’ 与期望值 y 之间的差异，即损失函数计算单个训练实例的误差：

L(y'^{(i)},y^{(i)})= (y'^{(i)}-y^{(i)})^2/2

L(y'^{(i)},y^{(i)})= -y^{(i)}log(y'^{(i)})+(1-y^{(i)})log(1-y'^{(i)})

成本函数

成本函数是整个训练集的损失函数的平均值，我们要找到使得总成本函数最小化的参数w和b。

---

梯度下降法

梯度

在微积分里面，对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度。比如函数f(x,y), 分别对x,y求偏导数，求得的梯度向量就是(∂f/∂x, ∂f/∂y)^T,简称grad f(x,y)或者▽f(x,y)。对于在点(x0,y0)的具体梯度向量就是(∂f/∂x0, ∂f/∂y0)^T.或者▽f(x0,y0)，如果是3个参数的向量梯度，就是(∂f/∂x, ∂f/∂y，∂f/∂z)^T,以此类推。　　　　
那么这个梯度向量求出来有什么意义呢？他的意义从几何意义上讲，就是函数变化增加最快的地方。具体来说，对于函数f(x,y),在点(x0,y0)，沿着梯度向量的方向就是(∂f/∂x0, ∂f/∂y0)T的方向是f(x,y)增加最快的地方。或者说，沿着梯度向量的方向，更加容易找到函数的最大值。反过来说，沿着梯度向量相反的方向，也就是 -(∂f/∂x0, ∂f/∂y0)^T的方向，梯度减少最快，也就是更加容易找到函数的最小值。

梯度下降与梯度上升

在机器学习算法中，在最小化损失函数时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数，和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。　　　　
梯度下降法和梯度上升法是可以互相转化的。比如我们需要求解损失函数f(θ)的最小值，这时我们需要用梯度下降法来迭代求解。但是实际上，我们可以反过来求解损失函数 -f(θ)的最大值，这时梯度上升法就派上用场了。

梯度下降法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-4bpnMeaY-1594981557849)(https://cdn.jsdelivr.net/gh/yexihe-jpg/image/img/20200629192811.png)]

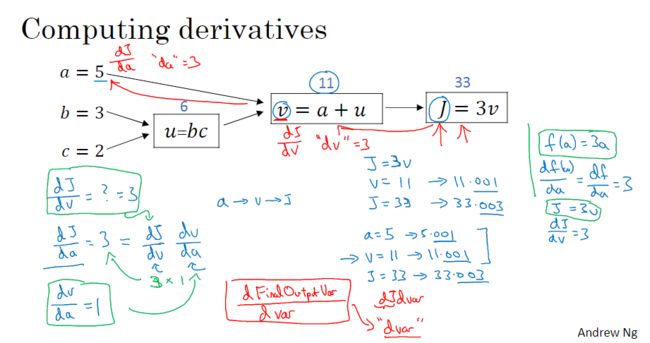
计算图

神经网络的计算都是沿着向前或者向后传播的

---

logistic回归中的梯度下降法

m个样本的梯度下降法

全局函数是1到m项的损失函数的和的平均，它表明全局函数成本对w1的导数也同样是1到m项的损失函数对w1的导数的和的平均；

---

向量化（帮助摆脱for循环）

**向量化：**加速计算数据，取代for循环

---

---

未完待续…

=

参考教程

网易云课堂–吴恩达给你的人工智能第一课
莫烦Python Pytorch 教程系列