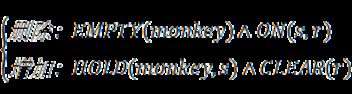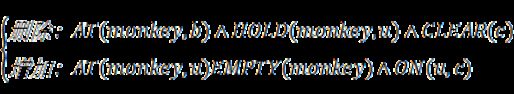广州大学人工智能原理实验一：知识的表示与推理实验
相关资料
广州大学人工智能原理实验一：知识的表示与推理实验
广州大学人工智能原理实验二：八数码问题
广州大学人工智能原理实验三：产生式系统推理
广州大学人工智能原理实验四：TSP问题的遗传算法实现
广州大学人工智能原理实验五：基于汉诺塔的问题规约图实现
五份实验报告下载链接
用谓词表示农夫、狼、山羊、白菜问题
-
-
- 相关资料
- 一、实验目的
- 二、基本要求
- 三、实验软件
- 四、实验内容：
-
- (一)猴子摘香蕉问题
- (二)传教士(牧师)与野人问题
- 五、实验源代码
-
- （一）猴子摘香蕉问题
- （二）传教士(牧师)与野人问题
- 六、实验结果及分析
- 七、最佳优先搜索BFS求解传教士(牧师)与野人问题
-
一、实验目的
本实验课程是计算机、智能、物联网等专业学生的一门专业课程，通过实验，帮助学生更好地掌握人工智能相关概念、技术、原理、应用等；通过实验提高学生编写实验报告、总结实验结果的能力；使学生对智能程序、智能算法等有比较深入的认识。本实验通过牧师与野人渡河的问题，强化学生对知识表示的了解和应用，为人工智能后续环节的课程奠定基础。
二、基本要求
1.实验前，复习《人工智能》课程中的有关内容。
2.准备好实验数据。
3.编程或验证需要独立完成，程序应加适当的注释。
4.完成实验报告。
三、实验软件
使用C或C++（Visual studio平台等）,或其它语言,如matlab或Python。
四、实验内容：
(一)猴子摘香蕉问题
利用一阶谓词逻辑求解猴子摘香蕉问题：房内有一个猴子，一个箱子，天花板上挂了一串香蕉，其位置如图1所示，猴子为了拿到香蕉，它必须把箱子搬到香蕉下面，然后再爬到箱子上。请定义必要的谓词，列出问题的初始化状态（即下图所示状态），目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。（附加：从初始状态到目标状态的谓词演算过程。）
1.定义描述环境状态的谓词。
AT(x,w)：x在w处，个体域：x?{monkey}，w?{a,b,c,box}；
HOLD(x,t)：x手中拿着t，个体域：t?{box,banana}；
EMPTY(x)：x手中是空的；
ON(t,y)：t在y处，个体域：y?{b,c,ceiling}；
CLEAR(y)：y上是空的；
BOX(u)：u是箱子，个体域：u?{box}；
BANANA(v)：v是香蕉，个体域：v?{banana}；
2.使用谓词、连结词、量词来表示环境状态。
问题的初始状态可表示为：So：AT(monkey,a)?EMPTY(monkey)?ON(box,c)?ON(banana,ceiling)?CLEAR(b)?BOX(box)?
BANANA(banana)
要达到的目标状态为：Sg：
AT(monkey,box)?HOLD(monkey,banana)?ON(box,b)?CLEAR(ceiling)?CLEAR©?
BOX(box)?BANANA(banana)
3.从初始状态到目标状态的转化, 猴子需要完成一系列操作, 定义操作类谓词表示其动作。
WALK(m,n)：猴子从m走到n处，个体域：m,n?{a,b,c}；
CARRY(s,r)：猴子在r处拿到s，个体域：r?{c,ceiling}，s?{box,banana}；
CLIMB(u,b)：猴子在b处爬上u；
这3个操作也可分别用条件和动作来表示。条件直接用谓词公式表示，是为完成相应操作所必须具备的条件；当条件中的事实使其均为真时，则可激活操作规则，于是可执行该规则中的动作部分。动作通过前后状态的变化表示，即通过从动作前删除或增加谓词公式来描述动作后的状态。
WALK(m,n)：猴子从m走到n处
条件：AT(monkey,m)
动作：
CARRY(s,r)：猴子在r处拿到s
条件：AT(monkey,r)?EMPTY(monkey)?ON(s,r)?BOX(box)?BANANA(banana)
动作：
CLIMB(u,b)：猴子在b处爬上u
条件：AT(monkey,b)?HOLD(monkey,u)?CLEAR(b)?BOX(box)?BANANA(banana)
动作：
4.按照行动计划, 一步步进行状态替换, 直至目标状态
AT(monkey,a)?EMPTY(monkey)?ON(box,c)?ON(banana,ceiling)?CLEAR(b)?BOX(box)?
BANANA(banana)
AT(monkey,c)?EMPTY(monkey)?ON(box,c)?ON(banana,ceiling)?CLEAR(b)?BOX(box)?
BANANA(banana)
AT(monkey,c)?HOLD(monkey,box)?ON(banana,ceiling)?CLEAR(b)?CLEAR©?BOX(box)?
BANANA(banana)
AT(monkey,b)?HOLD(monkey,box)?ON(banana,ceiling)?CLEAR(b)?CLEAR©?BOX(box)?
BANANA(banana)
AT(monkey,box)?EMPTY(monkey)?ON(box,b)?ON(banana,ceiling)?CLEAR©?BOX(box)?
BANANA(banana)
AT(monkey,box)?HOLD(monkey,banana)?ON(box,b)?CLEAR(ceiling)?CLEAR©?BOX(box)?
BANANA(banana)（目标得解）
猴子行动的规则序列是：WALK(a,c)→CARRY(c,box)→WALK(c,b)→CLIMB(box,b)→
CARRY(banana,ceiling)
(二)传教士(牧师)与野人问题
问题描述：
有n个牧师和n个野人准备渡河，但只有一条能容纳c个人的小船，为了防止野人侵犯牧师，要求无论在何处，牧师的人数不得少于野
人的人数(除非牧师人数为0)，且假定野人与牧师都会划船，试设计一个算法，确定他们能否渡过河去，若能，则给出小船来回次数最少的最佳方案。
实验步骤：
输入：牧师人数(即野人人数)：n；小船一次最多载人量：c。
输出：若问题无解，则显示Failed，否则，显示Successed输出所有可行方案，并标注哪一组是最佳方案。用三元组(X1, X2, X3)表示渡河过程中的状态。并用箭头连接相邻状态以表示迁移过程：初始状态->中间状态->目标状态。
例：当输入n=2，c=2时，输出：221->200->211->010->021->000；
其中：X1表示起始岸上的牧师人数；X2表示起始岸上的野人人数；X3表示小船现在位置(1表示起始岸，0表示目的岸)。
要求：写出算法的设计思想和源程序，并有用户界面实现人机交互（控制台或者窗口都可以），进行输入和输出结果，如：
Please input n: 2 Please input c: 2
Optimal Procedure: 221->200->211->010->021->000
Successed or Failed?: Successed
五、实验源代码
（一）猴子摘香蕉问题
#include （二）传教士(牧师)与野人问题
#include 六、实验结果及分析
（1）对于猴子摘香蕉问题根据自己编写代码或者参考代码，用不同的初始状态测试代码，记录每种初始状态下的输出结果，并对每个结果进行解释。
编写代码思路：使用DFS、递归遍历所有可能的情况并打印出来。香蕉对于猴子来说，不知道在哪里，所以对于猴子来说，要把下一步可能的情况都试一下，因为下一步有多种且是有限确定的走法，借助递归算法做出当前位置的判断，给出下一步的走法即可。
① 猴子在A，箱子在C，香蕉在B，不站在箱子上
结果分析：可以看到有4种路径都可以顺利摘到香蕉，最优的方法是第3种，只需4步。
② 猴子在C，箱子在C，香蕉在A，不站在箱子上
结果分析：可以看到有2种路径都可以顺利摘到香蕉，最优的方法是第2种，只需3步。
③ 猴子在B，箱子在B，香蕉在C，站在箱子上
结果分析：可以看到有2种路径都可以顺利摘到香蕉，最优的方法是第2种，只需4步。要先跳下箱子，再推动箱子，爬上去摘到香蕉。
④ 猴子在C，箱子在B，香蕉在A，站在箱子上
结果分析：猴子和箱子不在同一个位置上，不可能站在箱子上，所以这种初始状态不正确。
（2）完善猴子摘香蕉问题参考代码，参考代码中有什么问题？应该如何修改会更好。
① 递归使用错误，通过下图，可以看到代码出现了一些执行两步后，再调用自身，这种情况会导致第一次打印正确，但后面结果会打印错误的路线。这种情况应该直接修改nextstep()函数内的代码，使得递归正常。
② 该代码只考虑了香蕉在B的情况。在判断到达结束时，该代码给出了States[i].banana == 0限制了香蕉的位置，我们可以通过修改0为我们输入的位置，来获得更加多可能输入的情况。
③ 对于某些输入，打印结果错误。我们发现猴子在爬上箱子后，会直接获得香蕉，这种情况显然是不正确的，所以可以把获得香蕉这一步骤移至代码中的判断到达终点这一步骤，当猴子和箱子和香蕉在同一位置上，并且猴子在箱子上时，可获得香蕉。
④ 对于以上错误，我的代码均以全部纠正，并且完善了原代码的一些冗余地方。
（3）传教士(牧师)与野人问题，写出状态表示的数据结构，还有每种解的状态迁移图示。
typedef struct State //描述问题状态
{
int mLeft; //左岸传教士数量
int cLeft; //左岸野人数量
int mRight; //右岸传教士数量
int cRight; //右岸野人数量
int b; //船在左岸还是右岸
};
typedef struct Move //描述最优路线
{
char ch[1000]=""; //记录路线
struct Move* Next; //后向结点指针
};
两个传教士(牧师)与两个野人，小船一次最多载两人状态迁移图示
（4）尝试写出传教士(牧师)与野人问题的程序清单。
void nextStep(int i); /下一步，递归/
void showOptimal(); /输出最优路线/
void showSolution(int num); /打印所有路线/
void Empty(Move *point); /清空指针链表/
int Islegal(int num); /判断当前状态是否越界或不安全/
全部代码见第五部分——实验源代码
（5）实验结果讨论。
两个传教士(牧师)与两个野人，小船一次最多载两人
三个传教士(牧师)与三个野人，小船一次最多载三人
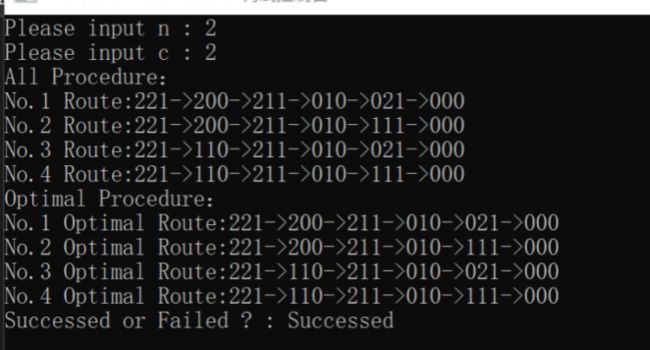
由于题目要求输出所有可能的路线，并输出最优的路线，所以使用DFS的递归实现无疑是最简单的实现算法，如果只要求最快地输出一种尽可能快的路线，我们可以使用BFS（最佳优先搜索）算法加快效率找到局部最优解。根据f(n)=h(n),h(n)选择左岸上牧师与野人的总数量可以尽可能快的找到局部最优解。
注：也可以修改估价函数变成实现A*算法，使f(n)=g(n)+h(n)，保证效率的前提下，寻得全局最优解。
七、最佳优先搜索BFS求解传教士(牧师)与野人问题
BFS（最佳优先搜索）效果如下：
使用的估价函数：
int Heruistic(STATUS *Node) //估价函数，左岸上牧师与野人数量越少，评价越高
{
return (Node->mLeft + Node->cLeft);
}
BFS（最佳优先搜索）代码如下：
#include