最大子序列和的四种算法实现(循序渐进)

ps：这是本人在武大图灵读书会上通过所读的《数据结构与算法分析——C语言描述》总结写成的，本来老师要求读的是《数学之美》，奈何我根本欣赏不了，于是果断掏出了我的这本书！

题目描述

给定整数数组arr[ ],用一个函数求${\sum }_{k=i}^j$arr[k]的最大值（若最大值仍为负数则返回0），即求任一arr的子序列和的最大值（子序列可以与原序列相同）
比如说一个数组{1,-2,4,5,-7,6,-4},它任一子序列和的最大值为9
怎么用代码求解呢？

问题求解

算法一

对一个问题，通常我们都可以用暴力破解法来求解，对这个问题也是如此，我们可以求出所有子序列的和，再从中找出最大的那一个，代码如下：

#include
int	subsequencesum_max(const int a[],int n)//subsequence是子序列的英文（我用百度翻译得到的），n是数组的大小
{
     
	int sum = 0, sum_max = 0,i=0,j=0,k=0;
	for (i = 0; i < n; i++)//为计算子序列和设置一个开始位置
	{
     
		for (j = i; j < n; j++)为计算子序列和设置一个结束位置
		{
     
			sum = 0;//每次计算后sum的值被改变，要重新赋值为0
			for (k = i; k <= j; k++)//计算该子序列的和
			{
     
				sum += a[k];
			}
			if (sum > sum_max)//如果该子序列的和>之前的最大值，则将最大值更新为该子序列之和
			{
     
				sum_max = sum;
			}
		}
	}
	return sum_max;
}

测试运行结果如下（测试案例在图中）：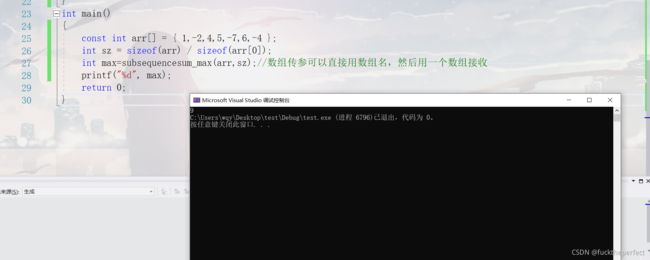
能写出来这题已经很不错了，但这种嵌套三个循环的算法的时间复杂度是O(n³),对于大量的运算，该算法耗费时间过长，不是一个很好的算法

算法二

仔细思考一番，我们会想到另一个比上一个算法好一些的暴力求解法，只用两个循环就可以遍历每一个子序列
代码如下：

int	subsequencesum_max(const int a[],int n)//subsequence是子序列的英文
{
     
	int sum = 0, sum_max = 0,i=0,j=0;
	for (i = 0; i < n; i++)
	{
     
		sum = 0;
		for (j = i; j < n; j++)//i是子序列的开始位置，一个for循环会遍历以i为开头的所有子序列，而外层循环会遍历所有i的值，因此这个嵌套循环可以遍历所有子序列
		{
     
			sum += a[j];
			if (sum > sum_max)
			{
     
				sum_max = sum;
			}
		}
	}
	return sum_max;
}

测试案例同上
这种算法的时间复杂度是O(n²)，比上面的算法稍好，但对大量数据处理还是不太行，但我们已经有进步了！

算法三

如果我们把这个数组分为两个部分，左半部分和右半部分，我们可以知道，该拥有最大值的子序列要么在左半部分，要么在右半部分，要么跨越两个部分（假设数组arr[ ]={4,-3,5,-2,-1,2,6,-2};）：
如图，最大的子序列可能出现在以上三个部位

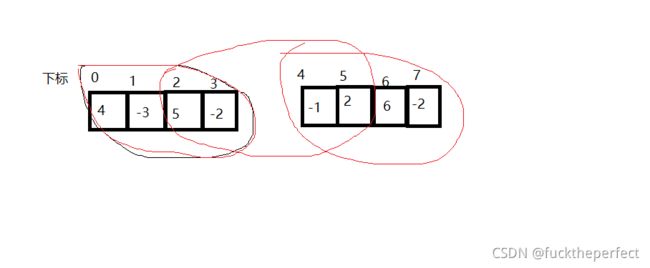
因此，我们可以求出左半部分的最大子序列，右半部分的最大子序列，和跨越两个部分的最大子序列，找出三者中的最大值，即为答案
有了以上的分析，我们可以用递归的思路来求解这道题：
代码如下：

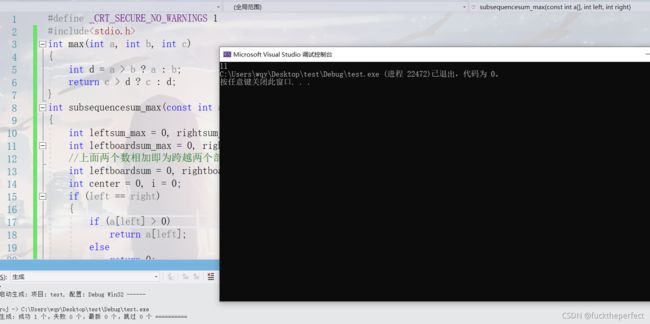
#include
int max(int a, int b, int c)
{
     
	int d = a > b ? a : b;
	return c > d ? c : d;
}
int	subsequencesum_max(const int a[],int left,int right)//subsequence是子序列的英文
{
     
	int leftsum_max = 0, rightsum_max = 0;
	int leftboardsum_max = 0, rightboardsum_max = 0;//其实这里是为了求跨越两个部分子序列最大值而用的小技巧，结合代码，带入实例，一步步分析，你就会明白它的作用
	//上面两个数相加即为跨越两个部分子序列的最大值，左边的数是从左半部分最右边的数字开始的，仔细理解这一点
	int leftboardsum = 0, rightboardsum = 0;
	int center = 0, i = 0;
	if (left == right)
	{
     
		if (a[left] > 0)
			return a[left];
		else
			return 0;
	}
	center = (left + right) / 2;
	leftsum_max = subsequencesum_max(a, left, center);
	rightsum_max = subsequencesum_max(a, center + 1, right);
	leftboardsum_max = 0;
	rightboardsum_max = 0;
	//用两个for循环分别求左半部分和右半部分的子序列和的最大值，注意第一个for循环开始位置
	for (i = center; i >= left; i--)
	{
     
		leftboardsum += a[i];
		if (leftboardsum > leftboardsum_max)
			leftboardsum_max = leftboardsum;
	}
	for (i = center+1; i <= right; i++)
	{
     
		rightboardsum += a[i];
		if (rightboardsum > rightboardsum_max)
			rightboardsum_max = rightboardsum;
	}
	return max(rightboardsum_max + leftboardsum_max, leftsum_max, rightsum_max);
}
int main()
{
     
	const int arr[] = {
     4,-3,5,-2,-1,2,6,-2};
	int sz = sizeof(arr) / sizeof(arr[0]);
	int max=subsequencesum_max(arr,0,sz-1);//数组传参可以直接用数组名，然后用一个数组接收
	printf("%d", max);
	return 0;
}

试图直接理解这块代码十分困难，我们可以代入案例并画图分析以了解其原理，就会发现这段代码其实是对该数组不断平分，并对每个小数组进行如下操作：求左半部分的最大子序列，右半部分的最大子序列，和跨越两个部分的最大子序列，找出三者中的最大值。而数组一直被平分就会有只剩一个元素的情况，此时只需特别写出这种情况的处理方式就可以了。
虽然这部分代码更让人望而生畏，但这种算法的时间复杂度是O(nlog n)，比前面两种都要好,最终运行结果也是正确的:

算法四

还有一种更简单的方法，我们只需要从数组的第一个数开始，依次加后面的数，一旦和为负数，就立即置为0，再继续加后面的数（第一个数也要判断是否是负数），因为一旦出现负数，有这一部分的序列必不可能是和最大的，因此把sum重新置为0，继续此循环，提示，带入实例更容易理解。
代码如下（实例同算法三）：

int	subsequencesum_max(const int a[],int n)//subsequence是子序列的英文
{
     
	int sum = 0, sum_max = 0;
	for (int i = 0; i < n; i++)
	{
     
		sum += a[i];
		if (sum > sum_max)
			sum_max = sum;
		else if (sum < 0)
			sum = 0;
	}
	return sum_max;
}

运行结果是正确的：


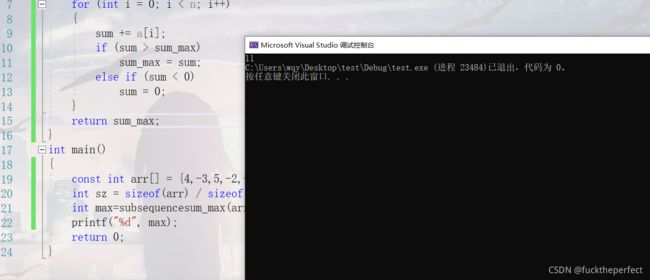
这块代码的时间复杂度是O(n),这种代码时间复杂度低，还很短很友好，真的太牛逼了，我们可以学习这种代码的思想，以武装自己。