KMP算法---C语言

---

字符串匹配

BF算法和KMP算法都主要是为了解决字符串匹配问题，即在主串（又叫文本串）（ primary string，简写为s）中寻找子串（又叫模式串） ( pattern string，简写为p)，其功能类似于strstr函数，与之不同的是strstr(str1,str2)返回值是一个指针，即返回 str1字符串从str2第一次出现的位置；否则，返回NULL。而BF算法和KMP算法则是返回子串在主串的下标，如果没找到则返回-1，当然如果想返回指针也很简单，只需要稍加修改代码即可。

此篇文章将以下面的主串和子串为例，来探讨BF算法和KMP算法的区别：

---

BF算法

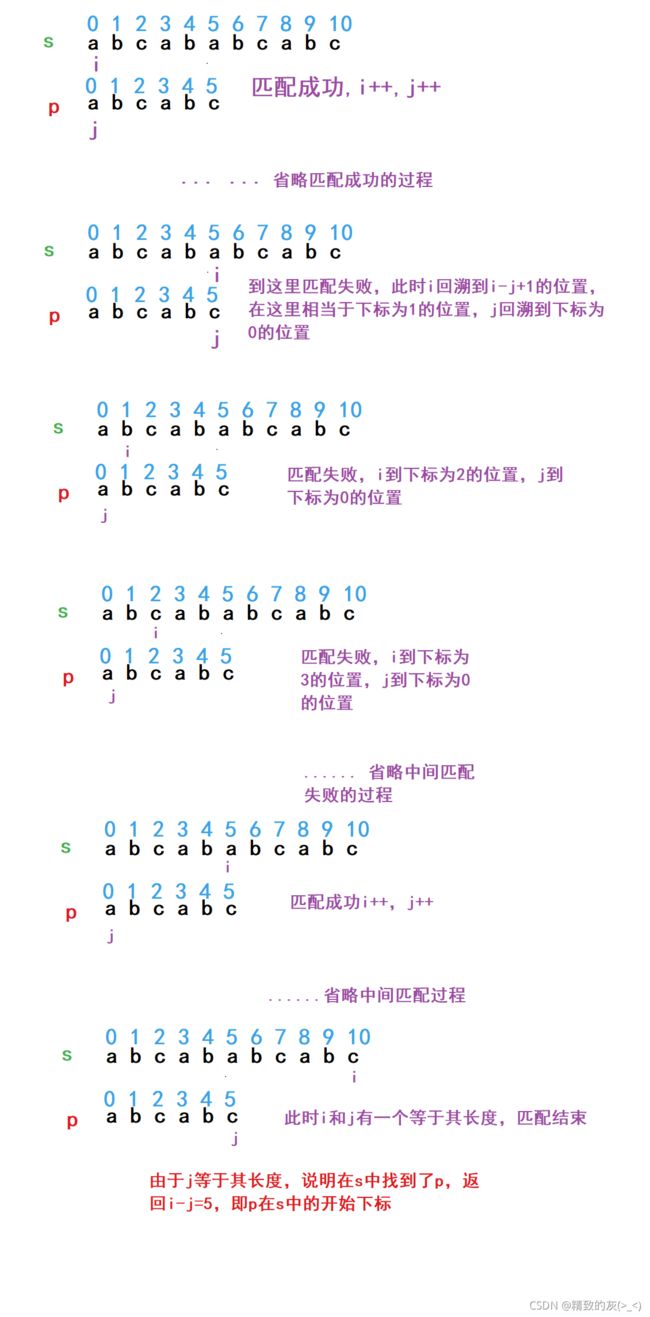
该算法采用暴力匹配的思路，假设主串s的下标为 i ，子串p的下标为 j ：

• 如果当前字符匹配成功（即s[i] == p[j]），则i++，j++，继续匹配下一个字符；
• 如果匹配不成功（即s[i]! = p[j]），令i = i - j + 1，j = 0。相当于每次匹配失败时，i 回溯，j 被置为0。由于匹配成功i和j共同自增，因此匹配失败相当于回溯到上一次回溯位置的下一个位置。

代码实现

int BfSearch(char* s, char* p)
{
     
	int sLen = strlen(s);
	int pLen = strlen(p);

	int i = 0;
	int j = 0;
	while (i < sLen && j < pLen)//等于其长度时就退出匹配
	{
     
		if (s[i] == p[j])
		{
     
			//匹配成功，i++，j++    
			i++;
			j++;
		}
		else
		{
     
			//如果失配，i回溯，j归零    
			i = i - j + 1;
			j = 0;
		}
	}
	//匹配成功，返回p在s中的位置，否则返回-1
	if (j == pLen)
		return i - j;
	else
		return -1;
}

测试：

BF算法的时间复杂度

最坏的情况是每次p匹配到最后一个位置匹配失败，s一直回溯，如果s的长度为n，p的长度为m，则时间复杂度为：O（n*m）

---

KMP算法

从上面的BF算法当中可以看到，当i第一次回溯以后，i和j匹配仍然失败，第三次回溯也是这样，这就导致了很多没有意义的匹配运算，效率十分低下。
观察s串和p串可以发现，当第一趟匹配失败时，其实i并不需要回溯，因为回溯了也会匹配失败，让j回溯即可。

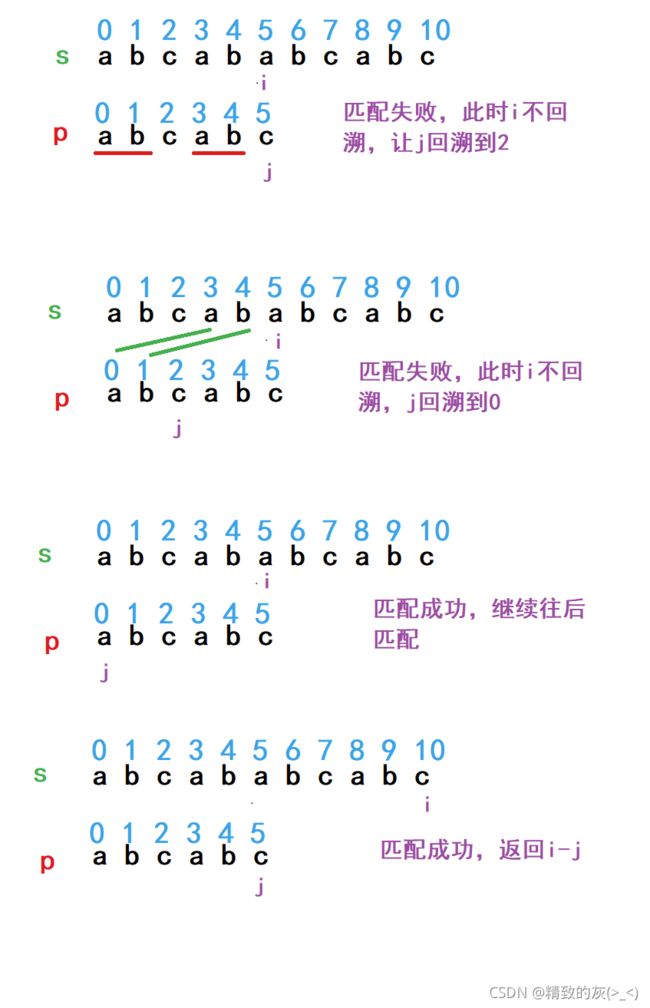
j为什么能回溯到下标为2的位置呢？这是因为在p串中，下标为0和1的位置与3和4的位置的字符相同，既然j能走到下标为5的地方，说明i前面的俩字符一定与j前面的俩字符匹配，那j回溯到下标为2的地方，回溯后前面的俩字符（下标为0和1）也一定i前面的俩字符匹配。
当j回溯到下标为2的位置以后，与i匹配失败，此时j回溯到下标为0的位置继续与i匹配，直到最后匹配成功。

到此为止，j如何回溯就成了我们需要解决的问题，我们将p每次回溯的下标位置存到一个名为next的数组中。

求next数组

next数组是与p传长度相同的int型数组，数组的每个位置记录了p串对应位置匹配失败后要回溯的下标。
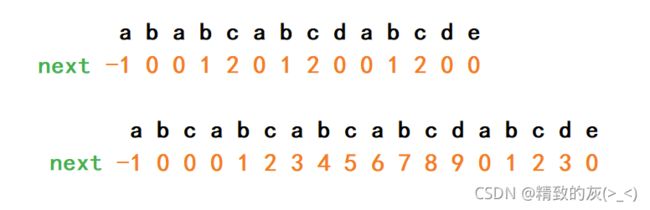
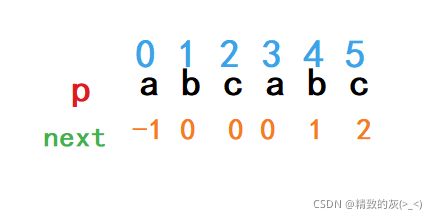
next数组中下标为x的位置存储的是p串以下标为0字符开头，以下标为x-1结束的两个（注意是两个，不是一个）长度最大（当有多个的时候，取长度最大的那两个）的相同子串的长度，比如

我们以同样的思路将其他位置的next找出，由于下标为0的位置只能回溯到它自己，所以我们将其设为-1（有的版本将其设为0）：

为了找出next数组的规律，我们再求两组：

仔细观察我们会发现一个规律，假设k=next[j]，如果p[j]=p[k]，那么next[j+1]=k+1，举个例子：

如果p[j]!=p[k]，就让k回退到next[next[ j ]]的位置，寻找长度更短的俩相同子串，如果还是p[j]!=p[k]，则让k回退到next[next[next[ j ]] ]的位置，直到回退到-1为止：

通过上面的分析，我们大致清楚了求next数组的思路：next[0]=-1（因为前面没有可以回溯的字符串），然后通过p[j]是否等于p[next[j]]的方式，来确定next[j+1]的值。

next数组的代码实现

void GetNext(char* p, int* next,int pLen)
{
     
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
     
		if (k == -1 || p[j] == p[k])
		{
     
				next[++j] = ++k;
		}
		else
		{
     
			k = next[k];
		}
	}
}

next数组的优化

到目前为止，next数组的实现已经完成，但next数组仍然存在一些不足，比如下面的情况：

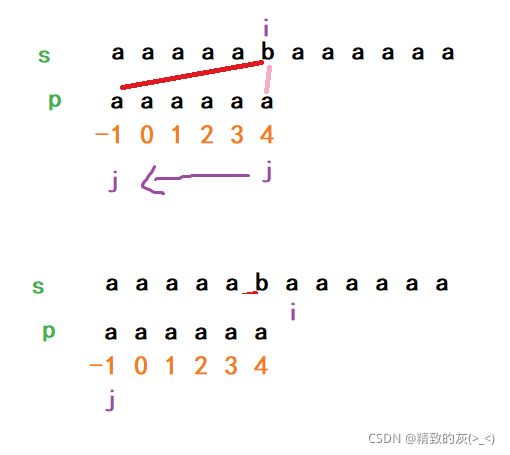
当s串中的b与p串中下标为5的a不匹配时，p会回溯到下标为4的a，但是这样仍然不匹配，一直回溯到下标为0的a，直到最后还是不匹配，i++。这主要是因为在确定next数组时忽略了p[j+1]==p[k+1]的情况，因为当s[i]!=p[j+1]时，s[i]!=p[k+1]，所以j回溯回去还是不相等，还是得继续往前回溯。为了解决这种问题，我们需要在p[j+1]==p[k+1]时继续往前回退，让next[j+1] = next[k+1]：

void GetNext(char* p, int* next,int pLen)
{
     
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
      
		if (k == -1 || p[j] == p[k])
		{
     
			++j;
			++k;
			if (p[j] != p[k])
				next[j] = k;
			else
				next[j] = next[k];
		}
		else
		{
     
			k = next[k];
		}
	}
}

KMP算法的代码实现

void GetNext(char* p, int* next,int pLen)
{
     
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < pLen - 1)
	{
     
		//p[k]表示前缀，p[j]表示后缀  
		if (k == -1 || p[j] == p[k])
		{
     
			++j;
			++k;
			if (p[j] != p[k])
				next[j] = k;
			else
				next[j] = next[k];
		}
		else
		{
     
			k = next[k];
		}
	}
}
int KmpSearch(char* s, char* p)
{
     
	int i = 0;
	int j = 0;
	int sLen = strlen(s);
	int pLen = strlen(p);
	//动态开辟next并调用函数求出next数组的值
	int* next = (int*)malloc(sizeof(int) * pLen);
	GetNext(p, next,pLen);
	while (i < sLen && j < pLen)
	{
     
		//如果j==-1说明s[i]和p[0]不匹配，此时应该让s[i+1]和p[0]匹配
		if (j == -1 || s[i] == p[j])
		{
     
			i++;
			j++;
		}
		else
		{
       //如果s[i] ！= p[j]就让j回溯
			j = next[j];
		}
	}
	//说明p串走完了，在s串中找到了p串
	if (j == pLen)
	{
     
		free(next);
		return i - j;
	}
	else
	{
     //说明s串走完但是p串没走完，s串中没有找到p串
		free(next);
		return -1;
	}
}

测试：

KMP算法的时间复杂度

最坏的情况是，当子串p的首字符位于主串s的第i - j的位置时才匹配成功，假设主的长度为n，子的长度为m，那么匹配过程的时间复杂度为O(n)，计算next的时间复杂度为O(m)，因此KMP算法的整体时间复杂度为O(n+m)。