第二轮 Python 刷题笔记一：数组

经过四十多天缓慢的刷题，现在进度大概是刷了八十多道 LeetCode 题，最近也在吸取过来人的经验，仍然需要对刷题计划进行调整。

首先明确下目标，我是有了 Python 基础，刷题是想掌握更多提升代码质量的算法、接触并了解更底层的原理和知识点。

结合着目标，便很快找到之前刷题过程中存在的不足：

1. 经常花费大量时间冥思苦想某道题，最终可能采用辛苦的方法做出来，就这么提交后没有继续跟进和整理，错过相关更巧妙算法知识的学习。
2. 之前的模式是刷完题后写题解，回顾下最初思路，代码实现加注释，比对下时间空间表现，时间充裕的话优化下——这就侧重点带偏到“完成任务”了，不过最近开始慢慢在调整
3. 从最初的按题号顺序刷，到之后按专题刷，对题目和类型的选择都太随意，缺乏系统和章法。

意识到这些，不妨把之前刷题规划到第一阶段，算是熟悉 LeetCode 题目和培养刷题习惯吧。接下来我们也将结合网上搜罗来的有效建议，对之后刷题模式做一番优化：

1. 遇到新题目，5-10 分钟考虑，有思路就代码实现，没有头绪则果断学习、模仿一直到可以独立写出题解
2. 题解要精简记录核心思路以及思路的转变过程，尤其是再遇到类似的如何去抓到思考点
3. 专题的选择更有条理，争取所有专题过一遍后，常见的题型都能涵盖，且相互间能加深联系
4. 新一轮刷题过程中，添加时间空间复杂度的分析，也要可以练习优化代码

以上便是暂时注意到的点，接下来开始第二轮的第一篇笔记~

之所以会对时间空间复杂度有所强调，一来是之前自己会觉得这个很难分析，二来是最近接触的几个算法课程开篇都是围绕复杂度展开的，学下来之后发现并没有想象中那么复杂。早学早好，掌握其知识点后，之后可以通过题目不断加深自己对复杂度的相关理解。

时间复杂度

时间复杂度通常表示为 O(f(n))，常见的 f(n) 有七种：常数复杂度 O(1)、对数复杂度 O(logn)、线性时间复杂度 O(n)、平方 O(n2)、立方 O(n3)、指数 O(2**n)、阶乘 O(n!)。

可能这时候我们第一轮的刷题会发挥作用了，回想之前接触到了诸多不同的算法：比如二分查找，其时间复杂度是 O(logn)：对 8 个数二分查找，通过 log2 8 = 3 次操作便可实现；再比如二叉树遍历，其时间复杂度是 O(n)，这里 n 是对应二叉树中所有节点，遍历所有节点即与 n 成线性关系。

这里值得注意的点是在时间复杂度中，常数系数是不考虑的，O(2n) 也是按 O(n) 来计。

空间复杂度

空间复杂度我们先简单理解：若涉及到数组，考虑数组的长度；若涉及到递归，则考虑递归的最大深度。二者均有，取其最大值。

后面配合着具体题目我们通过实践来加深理解。

题目一

LeetCode 第283题：移动零

难度：简单

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

示例:

输入: [0,1,0,3,12]
输出: [1,3,12,0,0]

说明:

必须在原数组上操作，不能拷贝额外的数组；尽量减少操作次数。

自行尝试

既然要移动所有 0，那么遍历整个数组是必须的；但不能拷贝额外数组，遍历过程中对数组的移动操作就要处理好。最基础的想法是遍历遇到 0 时删除该项，在结尾在补上 0，代码写出来这样：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:
        """
        Do not return anything, modify nums in-place instead.
        """
        # 因为删除元素会改变数组，这里采用 while 循环来控制遍历
        i = 0
        # count 用来记录检测到 0 的个数，也用来控制 while 的过程
        count=0
        # 当删除 0 时，数组的坐标会前移，最末位坐标为原坐标减去已检测 0 的个数
        while i<len(nums)-count:
        	# 若检测到 0
            if nums[i]==0:’
            	# 移除该位，此操作时间复杂度 O(n)
                nums.pop(i)
                # 结尾添 0，此操作时间复杂度 O(1)
                nums.append(0)
                # 已检测到的 0 个数 +1
                count+=1
            # 若未检测到0，移动到下一位
            else:
                i+=1

这是很简单直接的思路，但要注意到列表中 list.pop(i) 这种操作，删除掉 i 这位后，其后面的所有位都要前移，若 i 在最前，其时间复杂度是 O(n)，若每次遇到 0 都这么操作，时间复杂度是比较高的。

在此基础上优化的话，可以检测到 0 时，交换 0 与下一位非 0 的值。交换值的好处在于不用每次对其它值都进行操作，只在必要时进行调整。但可能会遇到连续出现 0 的情况，这就要有额外的标记来区分是 0 还是非 0 了。

首先就还是借用刚代码中的 count 变量记录检测到的 0 的个数，检测到 0 时，我们需要把这位换成下一个非 0 的数，此数的坐标即其原坐标减去其前面 0 的个数。换个理解，也可以是我们不再移动 0，而是将非 0 元素与其前面的 0 依次交换，代码实现：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:        
        # 方法二
        count = 0
        for i in range(len(nums)):
            if nums[i]==0:
                count += 1
            # 只有出现 0 才进行换位
            elif count>0:
                nums[i-count],nums[i] = nums[i],0

这里要注意只有出现了 0 才交换，即代码中检测非 0 时还要对 count 0 的个数做个判断。此外，同样的思路，我们只关注非 0 元素，将数组中非 0 的元素重新排到数组中，剩余的位置补上 0，代码实现：

class Solution:
    def moveZeroes(self, nums: List[int]) -> None:        
        #方法三
        j = 0
        for i in range(len(nums)):
            if nums[i]!=0:
            	# 通过 j 索引，只记录非 0 元素
                nums[j] = nums[i]
                j+=1
        # 剩余的位置全部赋为 0
        for k in range(j,len(nums)):
            nums[k] = 0

以上便是我能想到的思路和代码，接下来我们看下国外投票最高的 Python 题解代码。

学习题解

这个条经验是在算法训练课里看到的，在做完题目后，不妨去海外站上看下讨论区中投票最高的解法，这也是很好的学习别人优秀代码的实践。

# in-place
class Solution:
	def moveZeroes(self, nums):
	    zero = 0  # records the position of "0"
	    for i in range(len(nums)):
	        if nums[i] != 0:
	            nums[i], nums[zero] = nums[zero], nums[i]
	            zero += 1
# 来源：https://leetcode.com/problems/move-zeroes/discuss/72012/Python-short-in-place-solution-with-comments.

看完这个，其实和之前我们想到的利用 j 下标重组非 0 元素是相似的，但更妙的是代码直接将 nums[i] 和 nums[zero] 的值对调，这怎么理解呢？

首先，非 0 元素时，zero 和 i 一起递增，但如果下一位是 0，那么 nums[zero] 此时为 0，因为其最后有个 zero += 1；这样当再次遇到非 0 元素时，便可通过将 nums[zero] 和 nums[i] 互换，将 0 换到此刻的最末尾。这样遍历结束时便实现了将所有 0 后移。

交换值时间复杂度 O(1) 放在遍历过程中，整体时间复杂度是 O(n)，交换过程设计的是真的妙。但如果还是很难想通，不妨改写成如下：

class Solution:
	def moveZeroes(self, nums):
        # 方法四
        j = 0
        for i in range(len(nums)):
            if nums[i]!=0:
                nums[j]=nums[i] 
                # 若 i j 不等，说明有出现 0，将末位赋为 0               
                if i!=j:
                    nums[i]=0                
                j+=1

之前代码中 nums[zero] 作用是将 0 传递出去，这里我们直接将 nums[i] 赋值为 0 也是同样效果，但要有个对 i 和 j 的判断，只有二者不等时才这样补 0 至末位。

题目二

LeetCode 第26题：删除排序数组中的重复项

难度：简单

给定一个排序数组，你需要在 原地 删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。

示例 1:
给定数组 nums = [1,1,2], 
函数应该返回新的长度 2, 并且原数组 nums 的前两个元素被修改为 1, 2。 
你不需要考虑数组中超出新长度后面的元素。

示例 2:
给定 nums = [0,0,1,1,1,2,2,3,3,4],
函数应该返回新的长度 5, 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4。
你不需要考虑数组中超出新长度后面的元素。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array

自行尝试

注意题目中的数组是排过序的，基础想法是，遍历过程中检测到当前项与前一项相同时，移除该项，但无论是 pop(i) 还是 remove 其时间复杂度都是 O(n)，所以我们还是采用对原数组重新赋值的形式，利用额外的 k 索引，只在出现不同元素时 k 才增加、并更新 nums[k] 的值。遍历结束后，将 k 位之后的元素通过 pop() 来逐位删掉，注意，pop() 删最后一位的时间复杂度就是 O(1) 了，因为不会导致其他位置的改变。落实到代码：

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:
        j = 1
        for i in range(len(nums)):
            if i>0 and nums[i]!=nums[i-1]:
                nums[j] = nums[i]
                j+=1
        # 将最后多余的位删掉
        for k in range(j,len(nums)):
            nums.pop()
        return len(nums)

这样，在原数组上操作，时间复杂度控制在 O(n) 级别。

学习题解

观摩了点赞最高的 Python 题解，就是在刚我们代码基础上删掉后面的 pop() 的代码，直接返回 j：

class Solution:
    def removeDuplicates(self, nums: List[int]) -> int:      
        x = 1
        for i in range(len(nums)-1):
            if(nums[i]!=nums[i+1]):
                nums[x] = nums[i+1]
                x+=1
        return(x)
# 来源：https://leetcode.com/problems/remove-duplicates-from-sorted-array/discuss/302016/Python-Solution

感觉这是比较“鸡贼”，充分利用题目规则，因为题目规则中有个说明：

说明:
为什么返回数值是整数，但输出的答案是数组呢?

请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参做任何拷贝
int len = removeDuplicates(nums);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中该长度范围内的所有元素。
for (int i = 0; i < len; i++) {
     
    print(nums[i]);
}
#来源：力扣（LeetCode）
#链接：https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array

换言之，删不删后面的元素并不影响题目判断，所以不删除可以节省时间获得更好的表现。

同时，在参考中文题解时，会发现，这也被成为“双指针”、“快慢指针”，很明显，i 是遍历整个数组的“快指针”，我们额外定义的是有所筛选的“慢指针”，核心并不是指针如何去设计，而是具体过程中如何去操作的考虑。

题目三

LeetCode 第 70 题：爬楼梯

难度：简单

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

#来源：力扣（LeetCode）
#链接：https://leetcode-cn.com/problems/climbing-stairs

自行尝试

当积累一定刷题经验后，便很容易分辨出这是和斐波那契数列相关的题目，因为题目中呈现的规律是 f(n) = f(n-1) + f(n-2)。对于相关解法，看似省事的可能是递归，但其时间复杂度是 O(2^n) 指数级别，所以直接忽略不去考虑。比较常用的可能是如下两种解法，首先是用列表记录出现的项：

class Solution:
    def climbStairs(self, n: int) -> int:
    	# 列表记录前两项的值
        result = [1,1]
        # 从第三项开始循环
        for i in range(2,n+1):
        	# 当前项为前两项之和
            result.append(result[i-2]+result[i-1])
        # 返回所需要的项
        return result[n]

这里的操作是对数组遍历，其中的操作是 append()、O(1) 级别的，所以整体下来时间复杂度为 O(n)，额外建立了一个记录各项的列表，故空间复杂度也为 O(n)。常见继续优化的方式就是将这个列表给拿掉，因为我们每次只要记录前两项值即可，不用记录所有值，代码实现：

class Solution:
    def climbStairs(self, n: int) -> int:
		# 最初两项值
        a,b =1,1
        for i in range(n):
        	# 预先将 a+b 赋值给b，充当缓存，下次便可赋到 a 上
            a,b = b,a+b
        return a

这么下来，时间复杂度是 O(n)，空间复杂度就降到了常数级 O(1)。

这个解法可以熟记应用，推荐题解也基本是此写法或相应的变形。

通过如上的简单题目熟悉上手，接下来便是中等难度的两道题整理：

题目四

LeetCode 第 11 题：盛最多水的容器

难度：中等

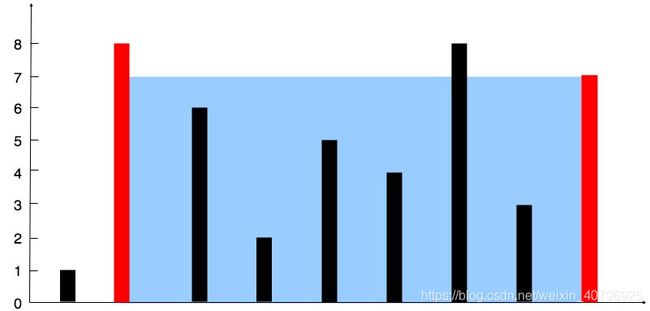
给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

示例：
输入：[1,8,6,2,5,4,8,3,7]
输出：49

自行尝试

这题目第一遍刷题时做过，现在就要结合回忆来阐述思路：采用双指针、双下标分别从最左和最右侧出发，记录此时左右边界较小的高度值作为容器高，坐标差为容器底，计算面积。要想获取更大的容积，在底在要变小的情况下，只能通过增加高度来实现，所以若指针处的高度不高于容器高，便可移动该指针。若左右指针可以生成更高的容器高，便可刷新容器高度，计算此时容积，若超过原容积则更新最大值、若未超出则继续移动指针，代码实现如下：

class Solution:
    def maxArea(self, height: List[int]) -> int:
    	# 左右边界双指针
        l,r = 0,len(height)-1
        # 容器高度取其中较小值
        h = min(height[l],height[r])
        # 底
        w = r-l
        # 容积或面积
        s = h*w
        # 指针循环
        while l<r:
        	# 若指针高度小于当前容器高，移动指针
            if height[l]<=h:
                l+=1
            elif height[r]<=h:
                r-=1
            # 若出现指针高度大于容器高
            else:
            	# 更新容器高
                h = min(height[l],height[r])
                # 更新容积最大值
                s = max(s,(r-l)*h)
        # 返回最大容积
        return s

我们也可以分析其复杂度：因为整个过程是对整个数组的遍历，其中操作只有移动指针、比较高度和计算的面积，整体下来时间复杂度 O(n)；没有额外的列表数组，所以空间复杂度为 O(1)。

参考题解

Python 题解中有份思路略不同的：

def maxArea(self, height):
    L, R, width, res = 0, len(height) - 1, len(height) - 1, 0
    for w in range(width, 0, -1):
        if height[L] < height[R]:
            res, L = max(res, height[L] * w), L + 1
        else:
            res, R = max(res, height[R] * w), R - 1
    return res
#来源：https://leetcode.com/problems/container-with-most-water/discuss/6131/O(N)-7-line-Python-solution-72ms

它这里是对底的长遍历，从最大的底开始一直到 0，也是对应我们之前双指针缩小范围的过程，这里的设计是，确定了底，来选高，计算面积，最终保留面积的最大值、高度的较小值。

题目五

LeetCode 第 15 题：三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例：

给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：
[
  [-1, 0, 1],
  [-1, -1, 2]
]
#来源：力扣（LeetCode）
#链接：https://leetcode-cn.com/problems/3sum

自行尝试

这题之前也做过，但再做却没思路了。能想到的就是先对数组排序，遍历确定第一个数，再其后面的列表元素中遍历确定第二个数，通过 0 减去二者的和得出第三个数的值，检测剩余列表是否存在第三个数。若存在，检测该组合是否出现过，若未出现，添加到结果中，返回最终结果。这解法搁在之前看到“超出时间限制”就不再多想了，现在正好分析下其时间复杂度：首先遍历第一个数 O(n)，此时遍历 for 中继续嵌套 for 来遍历第二个数，复杂度来到了 O(n^2)，在对第三数检测时，我们取巧可能采用 if third in rest_list 这种形式，但实际其复杂度仍很高，这么算下来应该是立方级别。此外，我们还需要检测结果中是否有该组合，若重复则不添加。整体下来，超时是理所当然的。

思考期间，并没能想到解法，虽然之前参考题解将这题解决了，但现在却一点印象都没。

参考题解

刚分析的时间复杂度为 O(n^3)，对第一个数遍历在所难免，但在接下来确定剩余两数过程，可以采用双指针法，以此将复杂度降到平方级别。同时，我们可以将数组先排序，这样在移动指针过程中，对重复出现的元素进行跳过，以此规避出现重复结果，从而不用检测结果中是否包含当前解，降低时间复杂度。

因为是参考了题解，所以惩罚自己重新默写代码来记忆：

class Solution:
    def threeSum(self, nums: List[int]) -> List[List[int]]:
    	# 先对列表排序，以此方便控制重复情况出现
        nums.sort()
        result = []
        # 第一个数索引为 i
        for i in range(len(nums)-2):
        	# x y 为后两个数的索引，双指针
            x,y = i+1,len(nums)-1
            # 若最小值为正或最大值为负，都不能出现和为 0，直接返回空列表
            if nums[i]>0 or nums[y]<0:
                return result
            # 若第一个数出现与先前一样，则跳过
            if i>0 and nums[i]==nums[i-1]:
                continue
            # 双指针循环
            while x<y:
            	# 当前三者组合
                temp = [nums[i],nums[x],nums[y]]
                # 三者和
                sum_3 = nums[i]+nums[x]+nums[y]
                # 若三数和为 0
                if sum_3==0:
                	# 加入到结果中
                    result.append(temp)
                    # 若第二、三项出现重复，不断移动其指针
                    while x<y and nums[x+1]==nums[x]:
                        x+=1
                    while x<y and nums[y-1]==nums[y]:
                        y-=1
                    # 此时再移动下双指针，使其不与当前项相等
                    x+=1
                    y-=1
                # 若和小于 0 ，移动 x 增加和
                elif sum_3<0:
                    x+=1
                # 若小于 0，左移 y 指针
                else:
                    y-=1
        return result

虽是重写，但其中还是有犯错的点，比如 if i>0 and nums[i]==nums[i-1]: 这里，是检测与之前一项是否相同，而不能检测与之后一项是否相同。因为比如 [-2,-1,-1,0,1,2] 若检测与之后一项相同跳过的话，就会把 [-1,-1,2] 的解遗失。以及在检测第二三项重复情况时，while x

代码来看的话，时间复杂度降到了 O(n^2)，因为第一层 for 之内的双指针移动是 O(n) 级别时间复杂度。空间复杂度的话，因为 result 是题目要求的列表，这个是必需的，理论上是不用考虑在内。

除此之外我们的 temp = [nums[i],nums[x],nums[y]] 看着是在 while 循环中，每次都生成一个列表，那么整个过程下来岂不占用了很多空间和无用的列表？这里正好运用下最近学到的 Python 语言中的垃圾回收机制：采用的是引用计数机制为主，标记-清除和分代收集两种机制为辅的策略。引用计数法中，当对象的别名被赋予新的对象时，旧对象引用计数 -1，在我们代码中就会被回收掉了，所以这里不用考虑因此导致的额外空间。

Python 垃圾回收机制介绍：https://testerhome.com/topics/16556

综合看来，空间复杂度是 O(1) ，接下来我们继续观摩下更优题解。

不得不佩服，点赞最高的题解自有其价值所在：

class Solution(object):
	def threeSum(self, nums):
        res = []
        nums.sort()
        length = len(nums)
        for i in range(length-2): #[8]
            if nums[i]>0: break #[7]
            if i>0 and nums[i]==nums[i-1]: continue #[1]
            l, r = i+1, length-1 #[2]
            while l<r:
                total = nums[i]+nums[l]+nums[r]

                if total<0: #[3]
                    l+=1
                elif total>0: #[4]
                    r-=1
                else: #[5]
                    res.append([nums[i], nums[l], nums[r]])
                    while l<r and nums[l]==nums[l+1]: #[6]
                        l+=1
                    while l<r and nums[r]==nums[r-1]: #[6]
                        r-=1
                    l+=1
                    r-=1
        return res
# 来源：https://leetcode.com/problems/3sum/discuss/232712/Best-Python-Solution-(Explained)

这是其代码，过程与我们的类似，当然，感觉我参考的题解可能最终来源也是这份代码，其说明中针对代码中注释的编号来解读。

First, we sort the array, so we can easily move i around and know how to adjust l and r.
If the number is the same as the number before, we have used it as target already, continue. [1]
We always start the left pointer from i+1 because the combination of 0~i has already been tried. [2]
Now we calculate the total:
If the total is less than zero, we need it to be larger, so we move the left pointer. [3]
If the total is greater than zero, we need it to be smaller, so we move the right pointer. [4]
If the total is zero, bingo! [5]
We need to move the left and right pointers to the next different numbers, so we do not get repeating result. [6]
We do not need to consider i after nums[i]>0, since sum of 3 positive will be always greater than zero. [7]
We do not need to try the last two, since there are no rooms for l and r pointers.
You can think of it as The last two have been tried by all others. [8]

此外对时间空间复杂度的分析上：

For time complexity
Sorting takes O(NlogN)
Now, we need to think as if the nums is really really big
We iterate through the nums once, and each time we iterate the whole array again by a while loop
So it is O(NlogN+N**2)~=O(N^2)
For space complexity
We didn’t use extra space except the res
So it is O(1).

时间复杂度：数组排序 O(nlogn)，第一层遍历数组 O(n)，双指针遍历 O(n)，总体 O(nlogn) + O(n) * O(n) 约为 O(n^2)，我们之前忽略了最初对列表的排序操作。

注：Python 中的 sort 和 sorted 排序内部实现机制为 Timsort，最坏时间复杂度为：O(n logn)，空间复杂度为 O(n)
参考链接：https://www.cnblogs.com/clement-jiao/p/9243066.html

但貌似看到的题解都没对排序的空间复杂度进行考虑，毕竟 sort 也没产生额外数组。

数组篇小结

因为是第二轮刷题，可能会更注重题目解法的整理和总结，五道题目中三道简单、两道中等难度，题目中多可以运用额外的列表空间或额外的指针来协助解决。结合着算法课程里面提到过要想降低时间复杂度，要么提升维度，要么空间来换取时间。

对数组类题目解决过程中，如果没思路，就先考虑暴力的穷举思路，对其中过程可以采取指针优化（比如题目五）。要有双指针的概念，以及在对数组操作过程中选取时间复杂度低的方法来实施。

这次整理比较长，没法做到每天一更，但学习效果会可能比之前的总结要更有效，所以近期会继续以类似的笔记完成第二轮对不同类型题目的整理，巩固以及提高刷题效果。