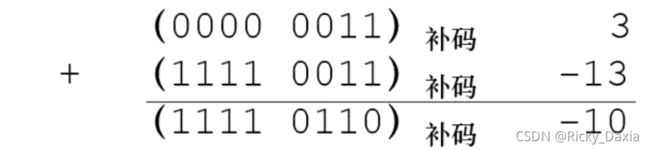你说你“码”呢
在计算机世界中,常用的计数系统有二进制、八进制、十进制和十六进制。十进制我们很常用,不再赘述。二进制我们也很熟悉,数由0或1组成,基数为2,逢二进一;八进制由0-7组成,基数为8,逢八进一;十六进制比较特别,由0-9和A、B、C、D、E、F组成,基数为16,逢十六进一。
对于每个进制之间的转换,先来看下以下的例子:
可以观察到最右位为基准进制的0次方,每往左一位次方加1,把乘积相加得到十进制数。
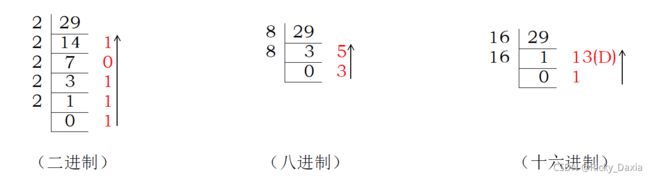
再看十进制转换成其他进制:
在转换过程中,我们不断除以基数,直到商为0,然后倒着取余数。
对于小数而言,二进制转换成十进制,我们看如下的例子:
我们把小数点后各位乘以基数的相应负幂次方,然后相加。
二进制转换成八/十六进制同样比较简单,以小数点为中心,向左和向右各以3或4位为一组(8对应2的3次方,16对应2的4次方),对于不足的,整数在左边补0,小数在右边补零,分别把每一组转换成对应进制数,例如:
十进制小数与二进制小数的转换过程分两步,整数部分同上,对于小数部分,可以把它连续乘以2,每次去掉结果的整数位,直到结果只包含整数为止。例如:
十进制小数转换成八进制和十六进制方法与以上类似,只需要把基数从2改成8或16即可,不谈。
在这里不妨思考一个问题:十进制的0.1用二进制表示是多少呢?这个数能用二进制精确表示吗?
可以看到,无论怎样乘下去,总不会出现结果为整数的情况。事实上,有一些数是不能用二进制精确表示的,如(0.1)10 = (0.000110011...)2 我们截取前9位,转换回十进制,结果如下:
计算机存数据并不像数学上那么精确,只有0.25、0.5、0.375、0.625这样的天选之子才能够被很好地表示。
在计算机中,数值的具体表示和存储方式通常会根据计算机的特点来设计。
下面来看 原码 和 补码:
整数的一种表示方法是用固定长度的二进制原码来表示,通常最高位表示它的正负号(0为正1为负),其他位表示数值的大小。如果用一个字节(byte)存储整数,就有八位,正数的最大范围是(0111 1111)即127。这时有同学可能会问,如果127 + 1,结果是多少呢?根据运算规则,128对应的二进制表示为(0 1000 0000),然而我们最多只能用8位来表示一个数,128却有9位,在这个运算过程中,数值溢出了。事实上,一个字节能够表示的整数范围是[-127,127],超出这个范围就会溢出。当然,我们可以用两个字节去表示,这样就可以表示更大范围的数啦!
如果说原码是为了解决正负号的存储问题,那么补码就可以用来解决减法运算的问题。
乍一看挺奇怪的,为什么要采取这样的定义呢?
首先我们要知道原码是存在一些弊端的:
1、0的原码是什么呢? 显然(0000 0000) 可以表示,可是(1000 0000)也可以表示呀,这就造成0的原码不唯一的问题。
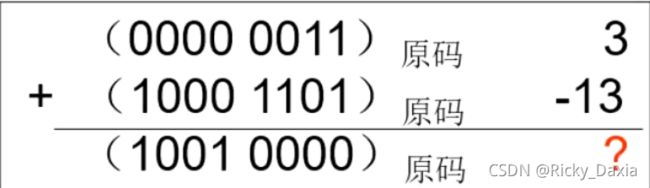
2、当机器计算减法的时候,根据四则运算法则,不够减的时候要向前一位“借位”,然而机器是喜欢往一个顺序算下去的,当我们要“借位”的时候,机器就很难受了。有同学就说了,我把减法变成加它的相反数的补码不就行了嘛?这个想法很好,但事实真的如此吗?来看这个例子:
3 - 13 相当于 3 + (-13),计算结果是(1001 0000),咦,这怎么成了-16呀...
可以看到,如果只采用原码来表示,其实是很不方便的。
这时候引入补码的概念,就可以发现,0的补码是(0000 0000),因为(1000 0000)为-128的补码,这就解决了0的表示不唯一的问题。
再看减法,对于 -13, 符号位为1,其他位的原码为(000 1101),各位取反得(111 0010),再末位加一得(111 0011),结果就是(1111 0011)。这时候我们做加法,得到的结果恰好就是-10的补码啦。
是不是很奇妙呢!
其实,在计算机里运算的时候,数据存储是有限制的,相当于在一个圆盘上计算,而不是在一条无限延伸的线上。我们可以通过这页课件来理解:
加法能到达的终点,通过减法也能到达。127往顺时针方向转127个格子到了126,它往逆时针转1个格子也能到126 => 127 + 127 等价于 127 - 1 。这个 127 是怎么来的呢?不就是128减去-1的绝对值吗!这就解释了公式的定义是怎么来的。-1的补码是多少?是(1111 1111),这不就是127的二进制表示嘛!
能够想出这样定义的人,是很聪明的。
下面来看 定点数(Fixed-point numbers) 和 浮点数(Floating-point numbers):
定点数的一些规则如下:
不过多讲,接下来看浮点数:
IEEE给出了浮点数内部表示的一个标准,它把实数表示成:![]() ,其中a称为尾数,b称为指数。
,其中a称为尾数,b称为指数。
看这页课件:
浮点数由4个部分组成,尾符表示正负号,阶码就是指数,尾数是小数部分。
对于十进制下的-0.5,首先转换成二进制-0.1,然后转换成规格化的方式,基数隐含存储,指数部分的用移码表示。
移码用一个字节存储,共128种组合,一些组合用来表示特殊情况。
下面看BCD码(Binary-coded decimal):
常用的8421 BCD码可以方便地在二进制和十进制进行转换,每个数字对应一串二进制数字。
这样的话就可以精确地表示一个数(只要给的数是正确的),BCD码常用于银行的会计系统。
除此之外还有ASCLL码,还有其他表示汉字的码制等等,有兴趣的时候再自行了解。
参考资料:
陈家骏、郑滔《程序设计教程-用C++语言编程》
《程序设计基础》课程资料