深度学习入门初探——多层感知机的神经网络式实现
这里将以前面两节的实现为基础,改进两个版本的代码,注意分析这两个代码和感知机实现的演进变化。
深度学习入门初探——感知机的初级理解
深度学习入门初探——简单的激活函数
在看源码之前,需要理解一下Numpy的几个乘法的区别:
对应元素相乘 : multiply 函数或 *
线性代数中矩阵乘法:dot函数或 matmul函数(二维与dot一样,可以支持更多的shape)
还有就是矩阵A*矩阵B和矩阵B*矩阵A可是不一样。可以看看代码中关于权重W2的处理,这里是偷了个懒不想变换了。
1 一版本代码
这版本代码是为了和异或门的多层感知机进行推演,在前向传播计算时(31行-41行)层级并未那么明显,但是权重和偏置还是很明显的层级定义的。
# coding: utf-8
import numpy as np
def init_network():
network = {}
network['W11'] = np.array([[-0.5], [-0.5]])
network['b11'] = np.array([0.7])
network['W12'] = np.array([[0.5], [0.5]])
network['b12'] = np.array([-0.2])
network['W2'] = np.array([0.5, 0.5])
network['b2'] = np.array([-0.7])
return network
def step_function(x):
return np.array(x > 0, dtype=int)
#def XOR(x1, x2):
# s1 = NAND(x1, x2)
# s2 = OR(x1, x2)
# y = AND(s1, s2)
# return y
def forward(network, x1, x2):
W11 = network['W11']
b11 = network['b11']
W12 = network['W12']
b12 = network['b12']
W2 = network['W2']
b2 = network['b2']
x = np.array([x1, x2])
# NAND
s11 = np.dot(x,W11) + b11
s11s= step_function(s11)
# OR
s12 = np.dot(x,W12) + b12
s12s= step_function(s12)
xtmp= np.array([s11s, s12s])
# AND
s2 = np.dot(W2,xtmp) + b2
y = step_function(s2)
return y
if __name__ == '__main__':
network = init_network()
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
res = forward(network, xs[0], xs[1])
print(str(xs) + " -> " + str(res))2 二版代码
这版本代码在前向传播计算时(31行-39行)层级就很明显了,其实这都是相较于目前一层神经网络和激活结合的概念来说的,两版代码后者实现的较为常见而已。
两层的神经网络,第一层两个神经元,第二层一个神经元。激活函数使用了阶跃函数。
# coding: utf-8
import numpy as np
def init_network():
network = {}
network['W11'] = np.array([[-0.5], [-0.5]])
network['b11'] = np.array([0.7])
network['W12'] = np.array([[0.5], [0.5]])
network['b12'] = np.array([-0.2])
network['W2'] = np.array([0.5, 0.5])
network['b2'] = np.array([-0.7])
return network
def step_function(x):
return np.array(x > 0, dtype=int)
#def XOR(x1, x2):
# s1 = NAND(x1, x2)
# s2 = OR(x1, x2)
# y = AND(s1, s2)
# return y
def forward(network, x1, x2):
W11 = network['W11']
b11 = network['b11']
W12 = network['W12']
b12 = network['b12']
W2 = network['W2']
b2 = network['b2']
x = np.array([x1, x2])
# NAND
s11 = np.dot(x,W11) + b11
# OR
s12 = np.dot(x,W12) + b12
xtmp= step_function(np.array([s11, s12]))
# AND
s2 = np.dot(W2,xtmp) + b2
y = step_function(s2)
return y
if __name__ == '__main__':
network = init_network()
for xs in [(0, 0), (1, 0), (0, 1), (1, 1)]:
res = forward(network, xs[0], xs[1])
print(str(xs) + " -> " + str(res))3 输出层
上面的输出就是结果,不做任何变化的输出即可,数学上称之为恒等函数吧。
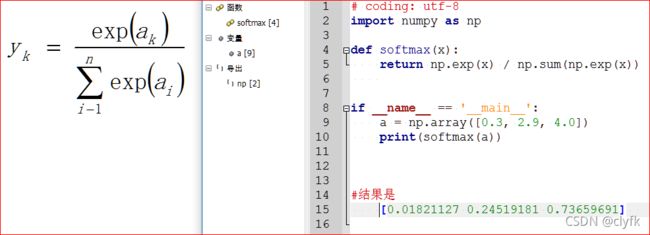
在机器学习的问题上可以大致地分为分类问题和回归问题。回归问题简言之就是根据某个输入来预测或计算出一个数值的结果,基本上使用的就是恒等函数;而分类问题是数据属于哪一个类别的问题,二分类和多分类等,使用的是softmax函数。
假设输出层共有n个神经元,计算第k个神经元的输出。分母是所有输入信号的指数函数的和,分子是输入信号的指数函数。
一般来说输出层都是全连接层,对于分类问题神经元的数量也都是类别的数量,输出层的各个神经元都会受到所有输入信号的影响。之所以会使用softmax函数,因为两个重要的特性:
输出的是0.0到1.0之间的实数,且总和为1;
各元素间的大小关系不变,因为指数函数时单调递增函数。
看到结果是否想到统计学中的概率了。