【机器学习】从零开始入门机器学习算法实践

人工智能热潮下，“大数据”、“机器学习”、“深度学习”热词屡见不鲜，但是想要真正掌握核心技术，势必要对机器学习算法有全面理解，这也是深入机器学习的必经之路。

 

为了让大家深入理解机器学习原理，11月22号，AI研习社邀请了日本名古屋大学陈安宁博士为大家奉上《从零开始入门机器学习算法实践》公开课，帮助大家对模型选择以及对数据分析有更全面理解，以提高在实际工作中选择算法的能力。

今天小编就带大家一起来回顾本节课程中陈博士分享的精彩内容。

浅谈机器学习

首先跟大家谈一下最近非常火热的几个名词：人工智能、机器学习、深度学习、神经网络，下图大致能反映出他们之间的关系：

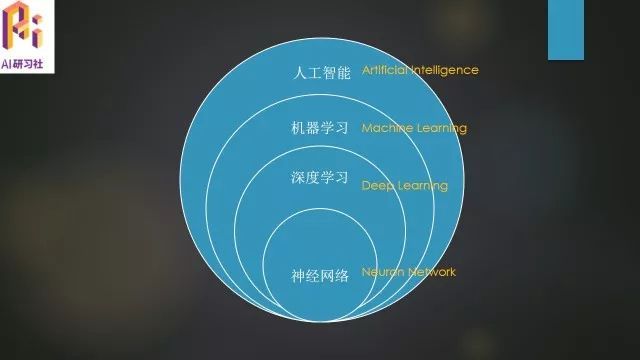
人工智能可以说是一个超复杂学科的集合，不仅包括了计算学科方面的知识，还包括了生物学科，社会学科等方面的内容，而机器学习只是它其中的一个分支，深度学习又是机器学习中的一个学习方向，最后，神经网络是深度学习里面目前应用的最广泛的一个学习方法。

其实对于机器学习的定义，可以说是仁者见仁智者见智，每个人在自己的领域可能都有不同的理解，我在这里给它的定义是：机器学习就是找出一种计算机算法，可以让计算机自己去处理新的问题。可能这个定义让大家觉得比较抽象，后面通过具体的算法介绍，会让大家更加容易理解。

 

那么，典型的机器学习过程是怎么样的呢？

其实就是包括三个部分，一是我们的输入过程，然后是模型，模型是过程中最重要的，也是我们一直在寻找和探究的，最后，就是输出的结果，这个结果可以有很多种，比如我们想预测的东西，想分类的事物等。

 

机器学习分类和应用

关于机器学习的分类，主要分为以下四种：监督学习，非监督学习，以及介于监督学习和非监督学习之间的半监督学习，另外还有强化学习。

监督学习：监督式学习的常用应用场景如分类问题（逻辑回归、决策树、KNN、随机森林、支持向量机、朴素贝叶斯）和回归问题（线性回归、KNN、Gradient Boosting&AdaBoost等等）

 

通俗点讲，就是监督学习的数据集内容是打了标签的，即已经给出了数据集结果的，通常我们在这种数据集上进行的模型探索就是监督学习。

 

可以看到，KNN既适用于分类问题，也适用于回归问题，也就是刚刚所说的，每种具体的算法适用的问题不是固定的，随着我们在各种模型的使用和问题的处理都有了一定的经验以后，我们才会采用更加合理的模型去应用和处理问题。

 

像上面这么多的模型，我本人最常用的是随机森林和支持向量机这两个模型，因为无论在什么情况下，这两个模型的效果都是非常好的。

 

非监督学习：常见的应用场景如聚类等。常见算法包括EM算法以及K-Means算法

 

相对监督学习来说，这是一个没有标签的数据集，我们只知道这里有一个数据集，但不知道这个数据集里的每个元素是什么，然后你要在这种情况下进行模型探索。      

 

半监督学习：介于监督学习和非监督学习之间，即数据集一部分是有标签的，一部分是没有标签的，它的探索方法基本就是从监督学习中改编和演变，以此来适应半监督学习的内容。      

 

强化学习：更强调与环境的互动，常见于动态场景或者机器人应用中，常见算法包括Q-Learning以及时间差学习（Temporal difference learning）

我们的《机器学习算法与实战入门基础》课程主要涉及到的还是监督学习和非监督学习两个部分的内容，而基本上学完这两个类别的算法，你也算是掌握了绝大部分的机器学习算法的基础铺垫了。

而在应用方面，目前机器学习已广泛应用于数据挖掘、计算机视觉、自然语言处理、语音识别、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、战略游戏和机器人等领域。

其中，计算机视觉、自然语言处理以及语音识别这三个方向可以说是目前最多人学习的一个方向，而在一直不被大家看好的证券市场分析方面，机器学习已经做的还不错了，我自己本身之前也是做数据挖掘和计算机图像处理，在课程里面，也会涉及这部分的分享内容。

两个基本概念

梯度（Gradient）

定义：即导数（Derivative），一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

过拟合（overfit）：Perfect sometimes is not good

过拟合主要就是说明并不是我们的模型用的越复杂就越好，这也是很多初学者易犯的错误，总认为参数给的越多，模型给的越复杂，效果会越好。在这里介绍这个概念也是为了给之后的入门课程做一个铺垫。

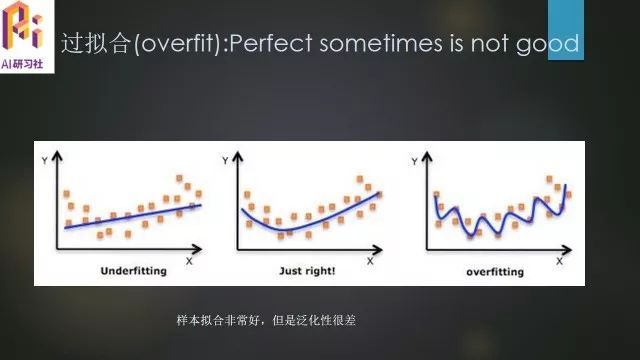
我们看上面三个数据集，中间的就是拟合的比较好的数据集，左边是欠拟合的数据集，而右边即是过拟合的数据集，我们在这里主要就是介绍右边这种。从图上看，可以看到样本曲线用的很复杂，拟合的非常好，细节处理的非常细致，但是泛化性很差，在整体的性能上会出现误差。

包括以后我们在课程的项目实训中都会提到这个问题，这个一方面是要看各种改善方法，另一方面就是要考不断的经验积累了。

 

算法

接下来就给大家讲一下算法方面的内容，也是我们的《机器学习算法与实战入门基础》中会讲到的最主要的内容。

 

期望最大算法（EM算法）

期望最大算法（EM算法）：Expectation-Maximization 算法是统计学中用来给带隐含变量的模型做最大似然（和最大后验概率）的一种方法。EM 的应用特别广泛，经典的比如做概率密度估计用的 高斯混合模型(Gaussian Mixture Model)。

明白一个概念，机器学习所有的算法只有一个目标，那就是找出目标函数的最大(小)值，所以EM算法肯定不是凭空出现的，它也是为了找出某个问题的最大(小)值

介绍这个算法之前，先给大家引出一个问题：

 

假设有三枚硬币A、B、C，每个硬币正面出现的概率是π、p、qπ、p、q。进行如下的掷硬币实验：先掷硬币A，正面向上选B，反面选C；然后掷选择的硬币，正面记1，反面记0。独立的进行10次实验，结果如下：1，1，0，1，0，0，1，0，1，1。假设只能观察最终的结果(0 or 1)，而不能观测掷硬币的过程(不知道选的是B or C)，问如何估计三硬币的正面出现的概率？(摘自李航老师《统计方法)

首先这个抛硬币问题其实是个二项分布问题，即伯努利分布。解答方法如下：

第一步，我们计算一个单独观察结果y的概率，就是最简单的二项分布，y的值只可能是0和1。

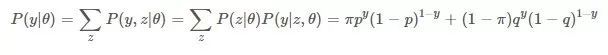
第二步，计算整个观测数据的概率，这个例子中我们总共有10个观测结果，所以n=10。

其实很简单，每个观测结果都是独立的，所以最终10个观测结果的概率就等于每个观测结果的概率相乘。

第三步 求参数模型的极大似然估计（极大似然估计的概念大家可以自行百度下）

所以我们的目标函数就有了：

（简单介绍一下这种书写方式。arg是argument是缩写，即自变数，参数的意思，max表示我们的目标是为了让后面的参数最大化。

所以这个式子的意思就是，求出能够让log函数最大的theta值。）

所以最终的目标函数变成：

提问：求y=x*x最小值时的x，写出上面形式的表达。

 

我们知道求最大最小值，最常用的办法就是求导，这个方法思路是以后机器学习算法的主要内容。

但是本问题的目标函数，不适用这个方法，因为目标函数过于复杂。那么，核心问题来了，怎么求呢？

 

为了让大家更直观地理解，小编直接在这里给大家奉上本次公开课的精彩视频：