【全文翻译】Domain Adaptation by Class Centroid Matching and Local Manifold Self-Learning
Domain Adaptation by Class Centroid Matching and Local Manifold Self-Learning
- Abstract
- 1. Introduction
- 2. Related Work
-
- A. Unsupervised Domain Adaptation
- B. Semi-supervised Domain Adaptation
- C. Local Manifold Learning
- 3. PROPOSED METHOD
-
- A. Notations 符号
- B. Problem Formulation 问题表述
- C. Optimization Procedure 优化步骤
- D. Convergence and Complexity Analysis 收敛性和复杂性分析
- 4. SEMI-SUPERVISED EXTENSION
- 5. EXPERIMENTS
-
- A. Datasets and Descriptions
- B. Experimental Setup
- C. Unsupervised Domain Adaptation
- D. Semi-supervised Domain Adaptation
- 5. CONCLUSIONS AND FUTURE WORK
- REFERENCES
Abstract
领域自适应已成为将知识从源领域转移到目标领域的一项基本技术。DA的关键问题是如何以适当的方式减少两个域之间的分布差异,以便可以对它们进行无差异的学习。与现有的独立对目标样本进行标签预测的方法不同,本文提出一种新颖的域自适应方法,该方法在两个域中的类质心的指导下为目标数据分配伪标签,从而使两者的数据分布结构可以强调源域和目标域。此外,为了更全面地探索目标数据的结构信息,我们进一步在建议中引入了局部连通性自学习策略,以自适应地捕获目标样本的固有局部流形结构。将上述类质心匹配和局部流形自学习集成到一个联合优化问题中,并设计了一种迭代优化算法以在理论上保证收敛。除了无监督域自适应以外,我们还以一种直接而又优雅的方式将我们的方法进一步扩展到半监督场景,包括同构和异构设置。在五个基准数据集上进行的大量实验以无监督和半监督的方式证明了我们的建议的显著优势。
1. Introduction
在许多实际应用中,数据通常是在不同条件下收集的,因此很难满足被称为统计学习理论基础的相同概率分布假设。这种情况自然会导致一个关键问题,即在经过良好标注的源域上训练的分类器无法直接应用于相关但不同的目标域。为了克服这个问题,作为迁移学习的重要分支,人们已经为领域适应做出了巨大的努力[1]。到目前为止,领域适应已成为跨域知识发现的一项基本技术,并且已在各种任务中得到考虑,例如对象识别[2],[3],面部识别[4],[5]和行人重识别[6]。

域自适应的主要问题是如何减少源域和目标域之间分布的差异[7]。最近的大多数工作旨在寻找一个共同的特征空间,该特征空间将跨域的分布差异最小化[8],[9],[10],[11],[12]。为了实现这一目标,已经提出了各种度量来测量分布差异,其中最大均值差异(MMD)[13]可能是使用最广泛的度量。基于MMD的方法的典型过程在每次迭代中包括三个关键步骤:
1)将原始源数据和目标数据投影到公共特征空间;
2)在投影源域上训练标准的监督学习算法;
3)使用源分类器为目标数据分配伪标签。
通常,此过程独立地对目标样本进行标签预测,忽略了两个域的数据分布结构,而这对于目标数据的伪标签分配至关重要。
为了更清楚地说明这一点,图1是一个小示例。红线是在投影特征空间中的源数据上训练的判别超平面。如我们所见,由于两个域之间的分布差异,超平面倾向于对目标数据进行错误分类。在这种情况下,分类错误的样本将严重误导后续迭代中对公共特征空间的学习,并最终导致明显的性能下降。实际上,从两个域中样本分布的角度来看,目标域中的类质心可以很容易地与源域中它们对应的类质心匹配。受此见解的启发,在本文中,我们打算引入一种新颖的方法,该方法在两个域中的类质心的指导下将伪标签分配给目标样本,而不是单独标记目标样本,这样可以强调源领域和目标领域的数据分布结构。为了实现这个目标,要处理的第一个关键问题是在缺少标签的情况下如何确定目标域的类质心。对于这个问题,我们采用经典的K-means聚类算法[14],该算法已广泛用于将未标记的数据划分为几组,其中同一组中的相似样本可以由特定的聚类原型表示。直观地讲,通过K-means算法获得的聚类原型可以看作是目标域类质心的良好近似。获得目标数据的聚类原型后,可以将域自适应中的分布差异最小化问题重新表述为类质心匹配问题,可以通过最近邻搜索有效地解决该问题。
显然,在目标数据的聚类原型学习过程中,聚类原型的质量对于我们方法的性能至关重要。实际上,已经表明,如果利用局部流形结构,则可以显着提高聚类性能[15],[16]。然而,大多数现有的流形学习方法高度依赖于内置在原始特征空间中的预定义相似度矩阵[17],[18],因此由于维数灾难而可能无法捕获高维数据的固有局部结构。为了解决这个问题,受最近提出的自适应邻居学习方法的启发[19],我们引入了一种局部结构自学习策略。具体来说,我们根据投影的低维特征空间而不是原始高维空间中的局部连通性来学习数据相似性矩阵,从而可以自适应地捕获目标数据的固有局部流形结构。
在以上分析的基础上,自然提出了一种新的领域自适应方法,该方法可以利用类质心匹配和局部流形自学习(CMMS)的结合来充分利用数据分布结构。值得注意的是,最近,由于在实践中可能会有一些标记的目标样本,因此解决半监督域自适应(SDA)问题的需求正在增长。[20], [21], [22], [23], [24]。尽管已经建立了无监督域自适应(UDA)方法,但大多数方法自然不能应用于半监督方案。令人兴奋的是,CMMS可以以直接却优雅的方式扩展到SDA,包括同构和异构设置。我们提出的CMMS的流程图如图2所示。本文的主要贡献概述如下:
•我们提出了一种新的领域自适应方法,称为CMMS,它可以通过联合类质心匹配和局部流形自学习来彻底探索数据分布的结构信息。
•我们提出了一种有效的优化算法,可以解决提案的目标功能,并具有理论上的收敛性保证。
•除了无监督域自适应以外,我们还将方法扩展到半监督场景,包括同构和异构设置。
•我们在五个基准数据集上对我们的方法进行了广泛的评估,这以无监督和半监督的方式验证了我们方法的优越性能。
本文的其余部分安排如下。第二节介绍了一些相关文献。第三节介绍了我们提出的方法,优化算法,收敛性和复杂性分析。我们将在第四节中描述我们的半监督扩展。大量的实验结果显示在第五节中。最后,我们在第六节中总结了本文。
2. Related Work
A. Unsupervised Domain Adaptation
B. Semi-supervised Domain Adaptation
C. Local Manifold Learning
3. PROPOSED METHOD
在本节中,我们首先介绍贯穿本文使用的符号和基本概念。然后,描述了我们的方法的细节。接下来,设计了一种有效的算法来解决我们建议的优化问题。最后,给出了优化算法的收敛性和复杂性分析。
A. Notations 符号
域D包含特征空间χ和边际概率分布P(X),其中X∈χ。对于特定领域,任务T由标签空间Y和标签函数f(x)组成,用T = {Y,f(x)} [1]表示。为简单起见,我们分别使用下标s和t来描述源域和目标域。
我们将源域数据表示为 D s D_s Ds = { X s , Y s X_s,Y_s Xs,Ys} ={ ( x s i , y s i ) (x_{si},y_{si}) (xsi,ysi)} i = 1 n s ^{n_s}_{i=1} i=1ns,其中 x s i ∈ R m x_{si}∈R_m xsi∈Rm是源样本, y s i ∈ R y_{si}∈R ysi∈R是相应的标签。类似地,我们将目标域数据表示为 D t D_t Dt= { X t X_t Xt} = { x t j x_{tj} xtj} j = 1 n t ^{n_t}_{j = 1} j=1nt,其中 x t j ∈ R m x_{tj}∈R_m xtj∈Rm。为了清楚起见,我们在表I中显示了本文中使用的主要符号和相应的描述。

B. Problem Formulation 问题表述
我们CMMS的核心思想在于通过两个域的类质心匹配以及对目标数据的局部流形结构自学习来强调数据分布结构。 CMMS的总体框架可以用以下公式表示:

第一项Ω(P,F)用于匹配类质心。 Θ(P,F, G t G_t Gt)是投影空间中目标数据的聚类项。Ψ(P,S)用于捕获数据结构信息。 Φ(P)是避免过拟合的正则项。超参数α,β和γ用于平衡不同项的影响。接下来,我们将详细介绍这些项目。
1)对目标数据进行聚类:在我们的CMMS中,我们借用聚类的思想来获得可以被视为伪类质心的聚类原型。在这种情况下,可以获取目标数据的样本分布结构信息。为了实现此目标,可以使用各种现有的聚类算法作为候选对象。在不失一般性的前提下,为简单起见,本文采用经典的K-means算法获得聚类原型。因此,我们有以下公式:
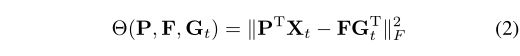
其中 P ∈ R m × d P∈R^{m×d} P∈Rm×d为投影矩阵, F ∈ R d × C F∈R^{d×C} F∈Rd×C是目标数据的聚类质心, G t ∈ R n t × C G_t∈R^{n_t×C} Gt∈Rnt×C是目标数据的聚类指标矩阵,如果 x t i x_{ti} xti的聚类标签为j,那么 ( G t ) i j (G_t)_{ij} (Gt)ij = 1,否则 ( G t ) i j (G_t)_{ij} (Gt)ij = 0。
2)两个域的类质心匹配:一旦获得了目标数据的聚类原型,我们就可以将域自适应中的分布差异最小化问题重新定义为类质心匹配问题。请注意,可以通过计算同一类别中样本特征的平均值来精确获取源数据的类别质心。在本文中,我们通过最近邻搜索解决了类质心匹配问题,因为它既简单又有效。具体来说,我们为每个目标聚类质心搜索最近的源类质心,并最小化每对类质心的距离之和。最后,将两个域的类质心匹配表示为:

其中 E s ∈ R n s × C E_s∈R^{n_s×C} Es∈Rns×C是一个常数矩阵,用于计算投影空间中源数据的类质心,如果 y s i = j y_{si} = j ysi=j则 E i j = 1 / n s j E_{ij} = 1 / n^j_s Eij=1/nsj ,否则 E i j = 0 E_{ij} = 0 Eij=0。
3)目标数据的局部流形结构自学习:在我们提出的CMMS中,目标样本的簇原型实际上是其对应类质心的近似值。因此,聚类原型的质量在我们的CMMS的最终性能中起着5个重要作用。现有工作已经证明,通过利用局部流形结构可以显著改善聚类的性能。然而,它们中的大多数高度依赖于原始特征空间中的预定义相邻矩阵,因此由于维数灾难而无法捕获高维数据的固有局部流形结构。对于这个问题,受近期工作的启发[19],我们建议在我们的CMMS中引入一种局部多方面的自学策略。代替在原始高维空间中预定义相邻矩阵,我们根据投影的低维空间中的局部连通性自适应地学习数据相似性,从而可以捕获目标数据的固有局部流形结构。局部流形自学习公式如下:

其中 S ∈ R n t × n t S∈R^{n_t×n_t} S∈Rnt×nt是目标域中的邻接矩阵,而δ是超参数。 L t L_t Lt是由 L t = D − S L_t = D-S Lt=D−S计算的对应图拉普拉斯矩阵,其中D是对角矩阵,每个元素 D i i = ∑ j ≠ i S i j D_{ii} = \sum_{j≠i}Sij Dii=∑j=iSij。
上面的描述突出了我们CMMS的主要组成部分。直观上,对源数据的合理假设是,同一类别的样本在投影空间中应尽可能接近,以便可以保留源域的区分结构信息。作为受[29]启发的一个微不足道但有效的技巧,我们将这种思想阐述如下:

其中tr(·)是迹运算符,并且

系数 1 / n s c 1 / n^c_s 1/nsc用于消除不同类别大小的影响[43]。
为简单起见,我们表示 X = [ X s , X t ] X = [X_s,X_t] X=[Xs,Xt]和 L = d i a g ( L s , L t ) L = diag(L_s,L_t) L=diag(Ls,Lt)。通过结合式(4)和式(5),我们得到了一个通用 Ψ ( P , S ) Ψ(P,S) Ψ(P,S)项,它可以捕获源领域数据和目标领域数据的各种结构信息:

此外,为避免过度拟合和提高泛化能力,我们还向投影矩阵P添加了F范数正则项:

到目前为止,通过结合公式(2)(3)(6)(7),我们得出了最终的CMMS公式:
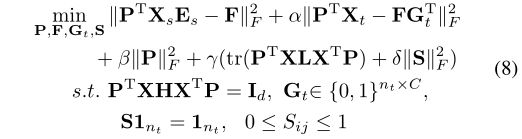
其中 I d I_d Id是d维的单位矩阵,H是定心矩阵,定义为 H = I n s + n t − 1 n s + n t 1 ( n s + n t ) × ( n s + n t ) H = I_{n_s + n_t}-\frac1{ n_s + n_t}1_{(n_s + n_t)×(n_s + n_t)} H=Ins+nt−ns+nt11(ns+nt)×(ns+nt)。 (8)中的第一个约束是受到主成分分析的启发,主成分分析旨在最大化投影数据的差异[9]。为了简化格式,我们将(8)中的目标函数重新编写为以下标准公式:
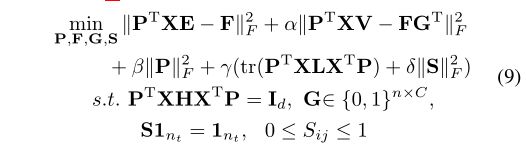
其中 n = n s + n t n = n_s + n_t n=ns+nt, V = d i a g ( 0 n s × n s , I n t ) V = diag(0_{n_s×n_s},I_{n_t}) V=diag(0ns×ns,Int), E = [ E s ; 0 n t × C ] E = [E_s; 0_{n_t×C}] E=[Es;0nt×C], G = [ 0 n s × C ; G t ] G = [0_{n_s×C}; G_t] G=[0ns×C;Gt], L = d i a g ( L s , L t ) L = diag(L_s,L_t) L=diag(Ls,Lt)。
C. Optimization Procedure 优化步骤
根据方程(9)中我们的CMMS的目标函数,有四个变量F,P,G,S需要优化。由于并非所有变量都同凸,因此在保持其他变量不变的情况下,我们交替更新每个变量。具体来说,每个子问题都按以下方式解决:
- F子问题:固定P,G和S时,优化问题(9)变为:

通过将相对于F的(10)的导数设置为0,我们得到:

- P子问题:将等式(11)代入等式(9)以替换F,我们可以得到以下子问题:

其中 R = E E T − E ( α G T G + I C ) − 1 ( E + α V G ) T + α V V T − α V G ( α G G T + I C ) − 1 ( E + α V G ) T R = EE^T-E(αG^TG+ I_C)^{-1}(E +αVG)^T +αVV^T-αVG(αGG^T+ I_C)^{-1}(E +αVG)^T R=EET−E(αGTG+IC)−1(E+αVG)T+αVVT−αVG(αGGT+IC)−1(E+αVG)T
。可以将上述问题转换为广义特征值问题,如下所示:

其中 Π= diag(π1,π2,…,πd)∈ R d × d R^{d×d} Rd×d对角矩阵,每个元素作为拉格朗日乘数。然后,通过计算方程对应于d最小特征值的特征向量来获得最优解。 - G子问题:在变量G中,仅需要更新 G t G_t Gt。在固定P,F和S的情况下,关于 G t G_t Gt的优化问题等于最小化公式(2)。像K-means聚类一样,我们可以通过将每个目标样本的标签分配给最近的聚类质心来解决它。为此,我们有:

- S子问题:当G,F和P固定时,关于S的优化问题等于最小化公式(5)。实际上,我们可以将其划分为与 n t n_t nt独立的子问题,每个子问题可表示为:

其中 S i , : S_{i,:} Si,:是S的第i行。通过定义 A i j = ∣ ∣ P T x t i − P T x t j ∣ ∣ 2 2 A_{ij} = ||P^Tx_{ti}− P^Tx_{tj}||^2_2 Aij=∣∣PTxti−PTxtj∣∣22,上述问题可以写成:
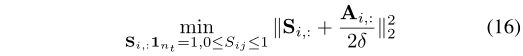
相应的拉格朗日函数为:

其中µ和η是拉格朗日乘数。
为了探索数据的局部性并减少计算时间,我们更倾向于学习稀疏的 S i S_i Si :,即仅保留每个样本的k近邻以进行局部连接。根据KKT条件,公式(17)具有一个闭式解:

其中 A ~ i j \widetilde Aij A ij是矩阵 A ~ \widetilde A A 的元素,是通过对A的每一行的条目按升序进行排序而获得的。根据[19],我们定义 B i j = ∣ ∣ x t i − x t j ∣ ∣ 2 2 B_{ij} = ||x_{ti}− x_{tj}||^2_2 Bij=∣∣xti−xtj∣∣22并将参数δ的值设置为:

与 A ~ i j \widetilde A_{ij} A ij相似,我们还将 B ~ i j \widetilde B_{ij} B ij定义为矩阵 B ~ \widetilde B B 的元素,该元素是通过将B的每一行的条目从小到大进行排序而获得的。
我们使用线性SVM1分类器初始化目标标签矩阵。通过求解原始空间中的每个子问题(如(16)),获得初始邻接矩阵。Algorithm 1中总结了CMMS的详细优化步骤。
Algorithm 1: CMMS for UDA
Input: 源数据{Xs,Ys};目标数据{Xt};初始目标标签矩阵Gt;
初始邻接矩阵S;超参数γ= 5.0,α,β;
子空间维数d = 100;邻域大小k = 10;最大迭代次数T = 10
Output: 目标标签矩阵Gt
1 t = 0;
2 while 不收敛 and t ≤ T do
3 // 投影矩阵P
4 通过解决(13)中的广义特征值问题更新P;
5 // 目标数据F的聚类原型矩阵
6 通过(11)更新F;
7 // 目标数据Gt的标签分配矩阵
8 通过(14)更新Gt的每一行
9 // 目标数据S的局部邻接矩阵
10 通过求解(16)更新S的每一行;
11 t = t + 1;
12 end
13 Return 目标标签矩阵Gt.
D. Convergence and Complexity Analysis 收敛性和复杂性分析
1)收敛性分析:我们可以通过以下命题证明算法1的收敛性:
命题1. 算法1中所示的拟议迭代优化步骤在每次迭代中单调减小了(9)的目标函数值。
证明. 假设在第r次迭代中,我们得到 P r , F r , G r , S r P_r,F_r,G_r,S_r Pr,Fr,Gr,Sr。在第r次迭代中,将(9)中目标函数的值表示为 f ( P r , F r , G r , S r ) f(P_r,F_r,G_r,S_r) f(Pr,Fr,Gr,Sr)。在我们的算法1中,我们将问题(9)划分为四个子问题(10),(12),(14)和(15),并且每个子问题相对于其相应变量都是凸问题。通过交替求解子问题,我们提出的算法可以确保找到每个子问题的最优解,即 P r + 1 , F r + 1 , G r + 1 , S r + 1 P_{r + 1},F_{r + 1},G_{r + 1},S_{r + 1} Pr+1,Fr+1,Gr+1,Sr+1。因此,作为四个子问题的组合,第(r +1)次迭代中的(9)的目标函数值满足:
![]()
鉴于此,证明完成,并且算法将至少收敛于局部解。
2)复杂度分析:我们的CMMS的优化算法1包含四个子问题。这四个子问题的复杂性归纳如下:首先,初始化S的成本为 O ( m n t 2 + n t 2 l o g ( n t ) ) O(mn^2_t + n^2_ tlog(n_t)) O(mnt2+nt2log(nt)),因此我们忽略了初始化 G t G_t Gt的时间,因为基本分类器非常快。然后,在每次迭代中,构造和求解P的广义特征值问题(12)的复杂度为 O ( n 2 C + n C 2 + C 3 + m n 2 + n m 2 + d m 2 ) O(n^2C + nC^2 + C^3 + mn^2 + nm^2 + dm^2) O(n2C+nC2+C3+mn2+nm2+dm2)。目标簇质心F的时间成本为 O ( d m n + d n C + d C 2 ) O(dmn + dnC + dC^2) O(dmn+dnC+dC2)。更新目标标签矩阵Gt的复杂度为 O ( C d n t ) O(Cdn_t) O(Cdnt)。以 O ( d n t 2 + n t 2 l o g ( n t ) ) O(dn^2_t + n^2_tlog(nt)) O(dnt2+nt2log(nt))为代价更新邻接矩阵S。通常,我们有C < d < m.因此,总体计算复杂度为 O ( n t 2 l o g ( n t ) ( T + 1 ) + n 2 m T + n m 2 T + d m 2 T ) O(n^2_tlog(nt)(T +1)+ n^2mT + nm^2T + dm^2T) O(nt2log(nt)(T+1)+n2mT+nm2T+dm2T),其中T为迭代次数。
4. SEMI-SUPERVISED EXTENSION
在本节中,我们将CMMS进一步扩展到半监督域自适应,包括同构和异构设置。
1)同构设置:我们将目标数据表示为 X t = { X l , X u } X_t = \{X_l,X_u\} Xt={ Xl,Xu},其中 X l = { x l i } i = 1 n l X_l = \{x_{li}\}^{n_l}_{i = 1} Xl={ xli}i=1nl是带有相应标签的标签数据,标签表示为 Y l = { y l i } i = 1 n l Y_l = \{y_{li}\}^{n_l}_{i = 1} Yl={ yli}i=1nl, X u = { x u j } j = 1 n u X_u = \{x_{uj} \}^{n_u}_{j = 1} Xu={ xuj}j=1nu是未标记的数据。在SDA方案中,除了源数据的类质心外,少数但精确的带标签目标数据可以为确定未带标签数据的聚类质心F提供额外的有价值的参考。在本文中,我们提供了一种简单而有效的策略来自适应地组合这两种信息。具体来说,我们提出的半监督扩展公式为:

式中 n t = n l + n u , λ 1 , λ 2 n_t = n_l + n_u,λ_1,λ_2 nt=nl+nu,λ1,λ2为平衡因子, G t = [ G l ; G u ] G_t = [G_l; G_u] Gt=[Gl;Gu]。 G l G_l Gl与 G s G_s Gs具有相同的定义。可以将等式(21)转换为标准公式,如等式(9)所示:

其中 E = [ λ 1 E s ; λ 2 E l ; 0 n u × C ] , G = [ 0 n s × C ; G t ] E = [λ_1E_s;λ_2E_l; 0_{n_u×C}],G = [0_{n_s×C}; G_t] E=[λ1Es;λ2El;0nu×C],G=[0ns×C;Gt]。除了平衡因子 λ 1 λ_1 λ1和 λ 2 λ_2 λ2之外,等式(22)中的其他变量也可以通过我们的算法1轻松求解。由于目标函数相对于 λ 1 λ_1 λ1和 λ 2 λ_2 λ2是凸的,因此可以使用封闭形式的解决方案轻松地求解它们:
λ 1 = m a x ( m i n ( t r ( J M T ) / t r ( J T J ) , 1 ) , 0 ) , λ 2 = 1 − λ 1 λ_1=max(min(tr(JM^T)/ tr(J^TJ),1),0),λ_2=1-λ_1 λ1=max(min(tr(JMT)/tr(JTJ),1),0),λ2=1−λ1,其中 J = P T X s E s − P T X l E l , M = F − P T X l E l J = P^TX_sE_s- P^TX_lE_l,M = F-P^TX_lE_l J=PTXsEs−PTXlEl,M=F−PTXlEl。
2) 异构设置:在异构设置中,源数据和目标数据通常具有不同的特征维数。我们提出的等式(21)可以自然地扩展到异构方式,只需用两个单独的投影矩阵替换投影矩阵P [24]:
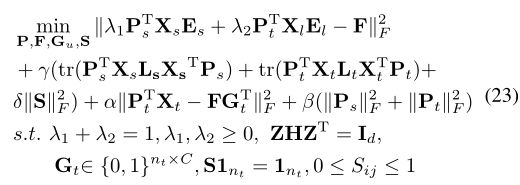
其中 Z = [ P s T X s , P t T X t ] Z = [P^T_sX_s,P^T_tX_t] Z=[PsTXs,PtTXt]是具有相同维的两个域的新特征表示。通过定义 X = d i a g ( X s , X t ) , P = [ P s ; P t ] X = diag(X_s,X_t),P = [P_s; P_t] X=diag(Xs,Xt),P=[Ps;Pt],可以将等式(23)转换为等式(22)的标准公式,从而可以用相同的算法求解。
5. EXPERIMENTS
在本节中,我们首先描述所有涉及的数据集。接下来,详细介绍了实验设置,包括UDA和SDA场景中的比较方法,训练协议和参数设置。然后,给出了在UDA场景下的实验结果,消融研究,参数敏感性和收敛性分析。最后,我们在SDA场景中显示结果。

A. Datasets and Descriptions
我们将我们的方法应用于在领域适应中广泛使用的五个基准数据集。这些数据集以不同种类的特征表示,包括AlexnetFC7,SURF,DeCAF6,Pixel,Resnet50和BoW。表II显示了这些数据集的总体描述。我们将详细介绍如下。
Office31 [44]包含来自以下三个域的31个类别的4,110个Office对象图像:Amazon(A),DSLR(D)和Webcam(W)。亚马逊图像是从在线商家下载的。 DSLR域中的图像由数码SLR相机捕获,而Webcam域中的图像则由网络相机捕获。我们采用在源域上微调的AlexNet-FC7features2。 [30]之后,我们有6个跨域任务,即“ A→D”,“ A→W”,…,“ W→D”。
Office-Caltech10 [10]在Office31数据集和Caltech256(C)数据集之间的10个共享类中包含2,533个对象的图像。 Caltech256数据集是对象识别广泛使用的基准。我们使用800像素的SURF功能3和4,096像素的DeCAF6功能4 [45]。根据[9],我们构造了12个跨域任务,即“ A→C”,“ A→D”,…,“ W→D”。
MSRC-VOC2007 [25]由两个子集组成:MSRC(M)和VOC2007(V)。它是通过选择MSRC中的1,269张图像和VOC2007中的1,530张图像而构建的,它们共有6种语义类别:飞机,自行车,鸟类,汽车,牛,绵羊。我们利用256像素像素功能。最后,我们建立两个任务,“ M→V”和“ V→M”。
Office-Home [46]涉及来自以下四个领域的65个共享类中的15585张日常对象图像:艺术(对象的艺术描绘,Ar),剪贴画(剪贴画图像的集合,Cl),产品(无背景的对象图像,Pr)和真实世界(使用常规相机拍摄的图像,Re)。我们使用[32]发布的4,096个Disnet50功能。类似地,我们获得12个任务,即“ Ar→Cl”,“ Ar→Pr”,…,“ Re→Pr”。
Multilingual Reuters Collection [47]是一种跨语言的文本数据集,包含来自六种常见类别的大约11,000篇文章,使用五种语言:英语,法语,德语,意大利语和西班牙语。所有文章均通过带有TF-IDF的BoW功能7进行采样。然后,它们由PCA处理以减小尺寸,而英语,法语,德语,意大利语和西班牙语的减小尺寸分别为1,131、1,230、1,417、1,041和807。我们依次选择西班牙语作为目标,其余每个作为来源。最终,我们获得了四个任务。
B. Experimental Setup
1)UDA场景中的比较方法:1-NN,SVM1,GFK [10],JDA [9],CORAL [12],DICD [29],JGSA [48],DICE [30],MEDA [27],SPL [32],MSC [31]。
2)SDA场景中的比较方法:SVMt,SVMst1,MMDT [20],DTMKL [49],CDLS [34],ILS [21],TFMKLS和TFMKL-H [22],SHFA [23],Li方法等。 [33]。 S V M t SVM_t SVMt, S V M s t SVM_{st} SVMst,MMDT,DTMKL-f,TFMKL-S和TFMKL-H用于同构设置,而 S V M t SVM_t SVMt,MMDT,SHFA,CDLS和[33]的方法用于异构设置。
3)训练协议:对于UDA场景,所有源样本都像[29]一样用于训练。我们在各种功能上采用z-score标准化[10]。对于SDA场景,在异构环境中,我们使用Office-Caltech10和MSRC-VOC2007数据集,遵循与[22]相同的协议。具体来说,对于Office-Caltech10数据集,我们为亚马逊域的每个类别随机选择20个样本,而为其他类别随机选择8个作为源。每个班级选择三个标记的目标样本进行训练,其余的则进行测试。为了公平起见,我们使用[20]发布的训练/测试拆分。对于MSRC-VOC2007数据集,所有源样本都用于训练,并且每个类别随机选择2或4个标记的目标样本进行训练,剩下的待识别。在异构环境中,我们使用[33]的实验设置来使用Office-Caltech10和Multilingual Reuters Collection数据集。对于Office-Caltech10数据集,SURF和DeCAF6功能用作源和目标。源域每个类包含20个实例,每个类别选择3个带标签的目标实例进行训练,其余的则进行测试。对于Multilingual Reuters Collection数据集,依次选择西班牙语作为目标,其余选择作为来源。每个类别随机选择100篇文章来构建源域,每个类别选择10篇带标签的目标文章进行训练,其余每类500篇文章进行分类。
4)参数设置:在UDA和SDA场景中,我们都没有大量标记的目标样本,因此我们无法执行标准的交叉验证程序来获取最佳参数。为了公平起见,我们引用原始论文的结果或运行作者提供的代码。按照[29],我们对超参数空间进行网格搜索,并报告最佳结果。对于GFK,JDA,DICD,JGSA,DICE和MEDA,可在d∈{10,20,…,100}中搜索最佳缩小尺寸。在{0.01,0.02,0.05,0.1,0.2,0.5,1.0}的范围内搜索投影的正则化参数的最佳值。对于最近的两种方法,SPL和MSC,我们采用其公共代码中使用的默认参数,或者按照相应的原始论文按照调整参数的过程进行操作。对于我们的方法,我们固定d = 100,γ= 5.0和k = 10,使得α,β可调。我们通过搜索α,β∈[0.01,0.02,0.05,0.1,0.2,0.5,1.0]获得最佳参数。
C. Unsupervised Domain Adaptation

1)UDA上的实验结果:Office31数据集上的结果。表III总结了Office31数据集上的分类结果,其中每个跨域任务的最高精度以黑体显示。我们可以观察到,CMMS具有最佳的平均性能,与最佳竞争对手MSC相比提高了1.1%。 CMMS在6个任务中的2个上获得最高结果,而MSC仅对任务A→W表现最佳,仅比CMMS高0.4%。通常,SPL,MSC和CMMS的性能要优于那些对目标样本进行独立分类的方法,这表明探索数据分布的结构信息可以促进分类性能。但是,与SPL和MSC相比,CMMS进一步挖掘和利用目标数据的固有局部流形结构来促进集群原型学习,从而可以实现更好的性能。

Office-Caltech10数据集上的结果。表IV中列出了具有SURF功能的Office-Caltech10数据集的结果。关于平均准确度,CMMS表现出很大的优势,与第二好的方法MEDA相比提高了1.7%。 CMMS是处理12个任务中的4个的最佳方法,而MEDA仅赢了2个任务。在C→A,D→A和C→W上,CMMS领先MEDA超过4.5%。继[32]之后,我们还使用了DeCAF6功能,分类结果如表V所示。就平均精度而言,CMMS优于所有竞争对手,并且除C→W以外,在所有任务上均表现最佳或次优。仔细比较SURF和DeCAF6features的结果,我们可以发现SPL和MSC更偏向于深层特征。但是,CMMS没有这样的偏好,这说明CMMS具有更好的泛化能力。

MSRC-VOC2007数据集上的结果。表VI中报告了MSRC-VOC2007数据集上的实验结果。 CMMS的平均分类准确度为55.4%,远高于所有竞争对手。特别是,在任务V→M上,与第二好的方法SPL相比,CMMS的性能提高了15.3%,这证明了我们建议的显着有效性。
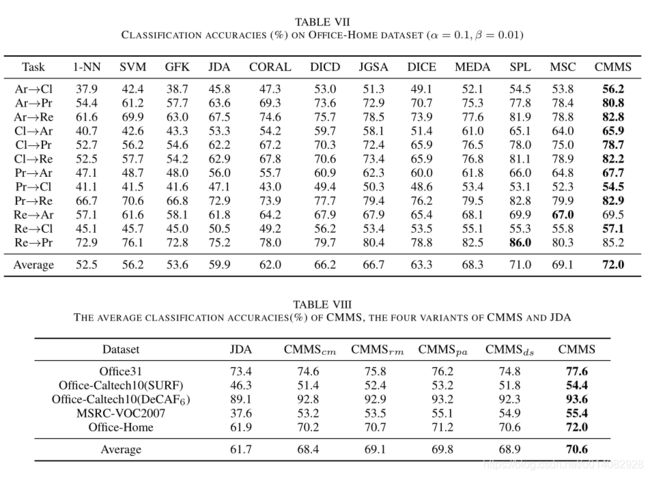
Office-Home数据集上的结果。为了公平起见,我们采用[32]最近发布的深层功能,这些功能是使用ImageNet上预训练的Resnet50模型提取的。表VII总结了分类的准确性。 CMMS在平均性能上胜过第二好的方法SPL,并且在所有12个任务中的10个上均达到了最佳性能,而SPL仅对Re→Pr任务表现最佳,仅比CMMS优越0.8%。这种现象表明,即使目标样本也很好地聚集在深层特征空间内,利用固有的局部流形结构对于提高分类性能仍然至关重要。
2)消融研究:为了更深入地了解我们的CMMS,我们提出了CMMS的四个变体:a)CMMS c m _{cm} cm,仅考虑两个域的类质心匹配,即等式(2),等式(3)和等式(7)的组合。; b)CMMS r m _{rm} rm不利用目标数据的局部流形结构,即从我们的目标函数公式(8)中删除公式(4); c)CMMS p a _{pa} pa,通过在原始特征空间中预定义邻接矩阵来考虑目标数据的局部流形结构,即用拉普拉斯正则化替换式(4); d)CMMS d s _{ds} ds通过将伪标签分配给目标数据来利用目标域的判别结构信息,然后最小化投影空间中的类内散布,如式(5)。表VIII显示了CMMS和所有变体的结果。还提供了经典JDA的结果。基于此表,我们将更详细地分析我们的方法,如下所示。
类质心匹配的有效性。 CMMS c m _{cm} cm在五个数据集上始终在JDA之前,这证实了我们的建议相对于基于MMD的开拓性方法具有明显的优越性。通过类质心匹配策略,可以充分利用数据分布的结构信息,从而使目标样本呈现良好的聚类分布。为了清楚地说明,在图3中,我们在MSRCVOC2007数据集的任务V→M的投影空间中显示了目标特征的t-SNE [50]可视化。我们可以观察到JDA特征混合在一起,而CMMS c m _{cm} cm特征与簇结构很好地分开,这证明了我们类质心匹配策略的显着有效性。

目标数据的局部流形自学习策略的有效性。 CMMS p a _{pa} pa在所有数据集上的表现均优于CMMS r m _{rm} rm,这表明即使目标流形结构不是那么可靠,利用目标样本的局部流形结构也可以更成功地对其进行分类。但是,如果我们可以更置信地捕获它,则可以实现卓越的性能,这可以通过将CMMS与CMMS p a _{pa} pa进行比较来验证。为了更好地理解,我们在图4中显示了任务A→D(SURF)上的目标邻接矩阵的可视化。这些矩阵是通过自学习距离或预定义距离(包括欧氏距离,内核宽度为1.0的热核距离)获得的和余弦距离。从图4中可以看出,所有预定义的距离都倾向于错误地连接不相关的样本,并且几乎无法捕获目标数据的固有局部流形结构。但是,自学习距离可以自适应地建立内在相似样本之间的联系,从而可以提高分类性能。通常,CMMS d s _{ds} ds的性能比CMMS差得多,甚至比CMMS r m _{rm} rm差,这证明通过单独将伪标记分配给目标样本来利用目标域的区分信息远远不足以取得令人满意的结果。原因是伪标签可能不准确,并且可能在学习过程中导致错误累积,因此性能急剧下降。综上所述,我们的局部流形自学习策略可以有效地提高目标数据中包含的结构信息的利用率。

3)参数敏感性和收敛性分析:在我们的CMMS中,有两个可调参数:α和β。我们对范围广泛的所有数据集进行了广泛的参数敏感性分析。我们一次更改一个参数,然后将其他参数固定为最佳值。 C→W(SURF),V→M,A→D(Alexnet7)和Ar→Pr的结果记录在图5(a)〜(b)中。同时,为了证明我们的CMMS的有效性,我们还以虚线显示了最佳竞争对手的结果。首先,我们运行CMMS,因为α在0.001到10.0之间变化。从图5(a)可以看出,当α的值非常小时,可能不会有助于性能的提高。而随着α的适当增加,目标数据的聚类过程得到了强调,因此我们的CMMS可以更有效地利用聚类结构信息。我们发现,当α处于较大范围[0.1,10.0]时,我们的提议可以始终如一地实现最佳性能。然后,我们通过将值从0.001更改为10.0来评估参数β对CMMS的影响。确定β的最佳值是不可行的,因为它高度依赖于数据集的领域先验知识。但是,根据经验,我们发现,当β处于[0.05,0.2]范围内时,我们的CMMS可以获得比最具竞争力的竞争对手更好的分类结果。我们还在图5(c)中显示了收敛性分析。我们可以看到CMMS可以在10次迭代中快速收敛。

D. Semi-supervised Domain Adaptation
1)同构设置的结果:表IX中显示了Office-Caltech10数据集上20种随机分割的所有方法的平均分类结果。我们可以观察到,相对于第二最佳方法TFMKL-S,在总体平均准确度方面,我们的CMMS可以提高0.8%。表X中显示了MSRC-VOC2007数据集上5个随机分开的结果。[22]中引用了一些结果。与大多数比较竞争对手相比,将每个类别中标记的目标样本数分别设置为2和4时,CMMS可以提高2.5%和2.6%。


2)异构环境中的结果:表XI和表XII中列出了Office-Caltech10和多语言的Reuters Collection数据集的结果。从[33]中引用了一些结果。我们可以观察到,就两个数据集而言,我们的CMMS均达到了最佳性能。具体而言,与最佳竞争对手相比,分别获得了1.5%和3.4%的改善。尤其是,CMMS在两个数据集上的所有10个任务中有8个工作得最好,这充分证实了我们CMMS在异构环境中的出色泛化能力。

5. CONCLUSIONS AND FUTURE WORK
本文提出了一种新的领域自适应方法CMMS。不同于大多数通常独立地将伪标签分配给目标数据的现有方法,CMMS通过源域和目标域的类质心匹配对目标样本进行标签预测,从而可以利用两个域的数据分布结构。为了更全面地探索目标数据的结构信息,在CMMS中进一步引入了局部流形自学习策略,该策略可以通过自适应地学习投影空间中的数据相似性来捕获目标数据的固有局部流形结构。 CMMS优化问题并非对所有变量都凸,因此设计了一种迭代优化算法来解决该问题,并仔细分析了其计算复杂性和收敛性。我们进一步将CMMS扩展到半监督方案,包括吸引人和有希望的同构和异构设置。在五个数据集上的大量实验结果表明,在无监督和半监督情况下,CMMS均明显优于baselines和几种最新技术。未来的研究将包括以下内容:1)考虑到CMMS优化的计算瓶颈,我们将为局部流形自学习设计更有效的算法; 2)除类质心外,我们可以引入其他度量来表示数据分布的结构,例如协方差; 3)在本文中,我们以直接但有效的方式将CMMS扩展到半监督方案。将来,更详细的半监督方法设计值得进一步探索。
REFERENCES
[1] S. J. Pan and Q. Yang, “A survey on transfer learning,” IEEE Trans.
Knowl. Data Eng., vol. 22, no. 10, pp. 1345-1359, Oct. 2010.
[2] Z. Guo and Z. Wang, “Cross-domain object recognition via input-output
kernel analysis,” IEEE Trans. Image Process., vol. 22, no. 8, pp. 3108-
3119, Aug. 2013.
[3] A. Rozantsev, M. Salzmann, and P . Fua, “Beyond sharing weights for
deep domain adaptation,” IEEE Trans. Pattern Anal. Mach. Intell., vol.
41, no. 4, pp. 801-814, Apr. 2019.
[4] C.-X. Ren, D.-Q. Dai, K.-K. Huang, and Z.-R. Lai, “Transfer learning
of structured representation for face recognition,” IEEE Trans. Image
Process., vol. 23, no. 12, pp. 5440-5454, Dec. 2014.
[5] Q. Qiu and R. Chellappa, “Compositional dictionaries for domain adap-
tive face recognition,” IEEE Trans. Image Process., vol. 24, no. 12, pp.
5152-5165, Dec. 2015.
[6] A. J. Ma, J. Li, P . C. Y uen, and P . Li, “Cross-domain person reiden-
tification using domain adaptation ranking SVMs,” IEEE Trans. Image
Process., vol. 24, no. 5, pp. 1599-1613, May 2015.
[7] M. Long, J. Wang, G. Ding, S. J. Pan, and P . S. Y u, “Adaptation
regularization: A general framework for transfer learning,” IEEE Trans.
Knowl. Data Eng., vol. 26, no. 5, pp. 1076-1089, May 2014.
[8] S. J. Pan, I. W. Tsang, J. T. Kwok, and Q. Yang, “Domain adaptation via transfer component analysis,” IEEE Trans. Neural Netw., vol. 22, no. 2, pp. 199-210, Feb. 2011.
[9] M. Long, J. Wang, G. Ding, J. Sun, and P . S. Y u, “Transfer feature
learning with joint distribution adaptation,” in Proc. IEEE Conf. Comput.
Vis. Pattern Recognit., Dec. 2013, pp. 2200-2207.
[10] B. Gong, Y . Shi, F. Sha, and K. Grauman, “Geodesic flow kernel
for unsupervised domain adaptation,” in Proc. IEEE Conf. Comput. Vis.
Pattern Recognit., Jun. 2012, pp. 2066-2073.
[11] B. Fernando, A. Habrard, M. Sebban, and T. Tuytelaars, “Unsupervised visual domain adaptation using subspace alignment,” in Proc. Int. Conf. Comput. Vis., Aus. 2013, pp. 2960-2967.
[12] B. Sun, J. Feng, and K. Saenko, “Return of frustratingly easy domain
adaptation,” in Proc. Amer . Assoc. Artif. Intell. Conf., 2016, pp. 2058- 2065.
[13] A. Gretton, K. M. Borgwardt, M. Rasch, B. Scholkopf, and A. J. Smola, “A kernel method for the two-sample-problem,” in Proc. Adv. in Neural Inf. Process. Syst., 2007, pp. 513-520.
[14] J. Macqueen, “Some methods for classification and analysis of multi-
variate observations,” in Proc. 5th Berkeley Symp. Math. Statist. Probab.,
1967, pp. 281-297.
[15] A. Goh and R. Vidal, “Segmenting motions of different types by
unsupervised manifold clustering,” in Proc. IEEE Conf. Comput. Vis.
Pattern Recognit., Jun. 2007, pp. 1-6.
[16] A. Goh and R. Vidal, “Clustering and dimensionality reduction on Rie-
mannian manifolds,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit.,
Jun. 2008, pp. 1-7.
[17] L. K. Saul and S. T. Roweis, “Think globally, fit locally: unsupervised
learning of low dimensional manifolds,” J. Mach. Learn. Res., vol. 4, pp.
119155, Dec. 2003.
[18] M. Belkin and P . Niyogi, “Laplacian eigenmaps and spectral techniques for embedding and clustering,” in Proc. Adv. Neural Inf. Process. Syst., Dec. 2001, pp. 585-591.
[19] F. Nie, X. Wang, and H. Huang, “Clustering and projected clustering
with adaptive neighbors,” in Proc. 20th ACM SIGKDD Int. Conf. Knowl.
Discovery Data Mining, 2014, pp. 977-986.
[20] J. Hoffman, E. Rodner, J. Donahue, B. Kulis, and K. Saenko, “Asymmetric and category invariant feature transformations for domain adaptation,” Int. J. Comput. Vis., vol. 41, nos. 1-2, pp. 28-41, 2014.
[21] S. Herath, M. Harandi, and F. Porikli, “Learning an invariant hilbert
space for domain adaptation,” in Proc. IEEE Conf. Comput. Vis. Pattern
Recognit., Jul. 2017, pp. 3845-3854.
[22] W. Wang, H. Wang, Z. X. Zhang, C. Zhang, and Y . Gao, “Semi-
supervised domain adaptation via Fredholm integral based kernel meth-
ods,” Pattern Recognit., vol. 85, pp. 185-197, Jan. 2019.
[23] W. Li, L. Duan, D. Xu, and I. W. Tsang, “Learning with augmented
features for supervised and semi-supervised heterogeneous domain adaptation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 36, no. 6, pp. 1134-1148, Jun. 2014.
[24] Y .-T. Hsieh, S.-Y . Tao, Y .-H. H. Tsai, Y .-R. Yeh, and Y .-C. F. Wang, “Recognizing heterogeneous cross-domain data via generalized joint distribution adaptation,” in Proc. IEEE Int. Conf. Multimedia Expo., Jul. 2016, pp. 1-6.
[25] M. Long, J. Wang, G. Ding, J. Sun, and P . S. Y u, “Transfer joint
matching for unsupervised domain adaptation,” in Proc. IEEE Conf.
Comput. Vis. Pattern Recognit., Jun. 2014, pp. 1410-1417.
[26] S. Chen, F. Zhou, and Q. Liao, “Visual domain adaptation using
weighted subspace alignment,” in Proc. SPIE Int. Conf. Vis. Commun.
Image Process., Nov. 2016, pp. 1-4.
[27] J. Wang, W. Feng, Y . Chen, H. Y u, M. Huang, and P . S. Y u, “Visual domain adaptation with manifold embedded distribution alignment,” in ACM Multimedia Conference on Multimedia 2018 ACM Multimedia Conf. Multimedia Conf., May 2018, pp. 402-410.
[28] L. Zhang. (2019). “Transfer adaptation learning: a decade survey.”
[Online]. Available: https://arxiv.xilesou.top/abs/1903.04687
[29] S. Li, S. Song, G. Huang, and Z. Ding, “Domain invariant and class
discriminative feature learning for visual domain adaptation,” IEEE Trans.
Image Process., vol. 27, no. 9, pp. 4260-4273, Sept. 2018.
[30] J. Liang, R. He, and T. Tan, “Aggregating randomized clustering-
promoting invariant projections for domain adaptation,” IEEE Trans.
Pattern Anal. Mach. Intell., vol. 41, no. 5, pp. 1027-1042, May 2019.
[31] J. Liang, R. He, Z. Sun and T. Tan, “Distant Supervised Centroid Shift: A Simple and Efficient Approach to Visual Domain Adaptation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2019, pp. 2975-2984.
[32] Q. Wang and T. P . Breckon. (2019). “Unsupervised domain adapta-
tion via structured prediction based selective pseudo-labeling.” [Online].
Available: https://arxiv.xilesou.top/abs/1911.07982
[33] J. Li, K. Lu, Z. Huang, L. Zhu, and H. Shen, “Heterogeneous domain
adaptation through progressive alignment,” IEEE Trans. Neural Netw.
Learn. Syst., vol. 30, no. 5, pp. 1381-1391, May 2019.
[34] Y .-H. H. Tsai, Y .-R. Yeh, and Y .-C. F. Wang, “Learning cross-domain landmarks for heterogeneous domain adaptation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2016, pp. 5081-5090.
[35] M. Xiao and Y . Guo, “Feature space independent semi-supervised
domain adaptation via kernel matching,” IEEE Trans. Pattern Anal. Mach.
Intell., vol. 37, no. 1, pp. 54-66, Jan. 2015.
[36] T. Yao, Y . Pan, C.-W. Ngo, H. Li, and T. Mei, “Semi-supervised domain adaptation with subspace learning for visual recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2015, pp. 2142-2150.
[37] D. Hong, N. Y okoya, and X. Zhu, “Learning a robust local manifold
representation for hyperspectral dimensionality reduction,” IEEE J. Sel.
Topics Appl. Earth Observ. Remote Ses…, vol. 10, no. 6, pp. 2960-2975,
Jun. 2017.
[38] K. Zhan, F. Nie, J. Wang, and Y . Yang, “Multiview consensus graph
clustering,” IEEE Trans. Image Process., vol. 28, no. 3, pp. 1261-1270,
Mar. 2019.
[39] C. Hou, F. Nie, H. Tao, and D. Yi, “Multi-view unsupervised feature
selection with adaptive similarity and view weight,” IEEE Trans. Knowl.
Data Eng., vol. 29, no. 9, pp. 1998-2011, Sept. 2017.
[40] W. Wang, Y . Yan, F. Nie, S. Yan, and N. Sebe, “Flexible manifold
learning with optimal graph for image and video representation,” IEEE
Trans. Image Process., vol. 27, no. 6, pp. 2664-2675, Jun. 2018.
[41] C.-A. Hou, Y .-H. H. Tsai, Y .-R. Yeh, and Y .-C. F. Wang, “Unsupervised domain adaptation with label and structural consistency,” IEEE Trans. Image Process., vol. 25, no. 12, pp. 5552-5562, Dec. 2016.
[42] J. Li, M. Jing, K. Lu, L. Zhu and H. Shen, “Locality preserving joint
transfer for domain adaptation,” IEEE Trans. Image Process., vol. 28, no.
12, pp. 6103-6115, Dec. 2019.
[43] S. Wang, J. Lu, X. Gu, H. Du, and J. Yang, “Semi-supervised linear
discriminant analysis for dimension reduction and classification,” Pattern
Recognit., vol. 57, pp. 179-189, Sept. 2016.
[44] K. Saenko, B. Kulis, M. Fritz, and T. Darrell, “Adapting visual category
models to new domains,” in Proc. Eur . Conf. Comput. Vis., 2010, pp.
213-226.
[45] J. Donahue, Y . Jia, O. Vinyals, J. Hoffman, N. Zhang, E. Tzeng, and
T. Darrell, “DeCAF: A deep convolutional activation feature for generic
visual recognition,” in Proc. Int. Conf. Mach. Learn., 2014, pp. 647-655.
[46] H. V enkateswara, J. Eusebio, S. Chakraborty, and S. Panchanathan,
“Deep hashing network for unsupervised domain adaptation,” in Proc.
IEEE Conf. Comput. Vis. Pattern Recognit., Jun. 2017, pp. 5018-5027.
[47] M.-R. Amini, N. Usunier, and C. Goutte, “Learning from multiple par-
tially observed views-an application to multilingual text categorization,”
in Proc. Adv. in Neural Inf. Process. Syst., Dec. 2009, pp. 28-36.
[48] J. Zhang, W. Li, and P . Ogunbona, “Joint geometrical and statistical
alignment for visual domain adaptation,” in Proc. IEEE Conf.Comput.
Vis. Pattern Recognit., Jun. 2017, pp. 1859-1867.
[49] L. Duan, I. W. Tsang, and D. Xu, “Domain transfer multiple kernel
learning,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 34, no. 3, pp.
465-479, Mar. 2012.14
[50] L. van der Maaten and G. Hinton, “Visualizing data using t-SNE,” J.
Mach. Learn. Res., vol. 9, pp. 2579-2605, Nov. 2008.
