Python 大白从零开始 OpenCV 学习课-6. 灰度变换与直方图处理

从零开始 OpenCV 学习课-6. 灰度变换与直方图处理

本系列面向 Python 小白，从零开始实战解说 OpenCV 项目实战。

空间域的图像处理方法直接对图像的像素点进行处理，空间域图像处理技术主要是灰度变换和空间滤波。

本节介绍图像的灰度变化与直方图处理，提供完整例程和运行结果：二值处理，反色变换，线性变换，分段线性变换，对比度拉伸，灰度级分层，非线性变换，直方图处理，直方图均衡化，直方图匹配，局部直方图处理，统计量增强，反向投影。

---

1. 图像增强技术

图像增强（Image Enhancement）的方法主要有空间域变换、频率域变换和伪彩色处理。

• 空间域变换：空间域是指图像平面，空间域的图像处理方法直接对图像的像素点进行处理。空间域图像处理技术主要是灰度变换和空间滤波。
• 频率域变换： 通过傅立叶变换，在频率域进行处理，然后再转换回空间域。
• 伪彩色处理：把灰度图像映射到彩色空间，常用于遥感图像、医学影像处理。

---

2. 图像的灰度化处理和二值化处理

按照颜色对图像进行分类，可以分为二值图像、灰度图像和彩色图像。

• 二值图像：只有黑色和白色两种颜色的图像。每个像素点可以用 0/1 表示，0 表示黑色，1 表示白色。
• 灰度图像：只有灰度的图像。每个像素点用 8bit 数字 [0,255] 表示灰度，如：0 表示纯黑，255 表示纯白。
• 彩色图像：彩色图像通常采用红色（R）、绿色（G）和蓝色（B）三个色彩通道的组合表示。

OpenCV 中彩色图像使用 BGR 格式。彩色图像进行灰度化处理，可以在读取图像文件时直接读取为灰度图像，也可以通过颜色空间转换函数 cv2.cvtColor 将彩色图像转换为灰度图像。

灰度化处理相关函数和例程介绍，详见 [OpenCV 学习课-2.图像读取与显示]。

# 1.1 图像的读取
    imgFile = "../images/imgLena.tif"  # 读取文件的路径
    img1 = cv2.imread(imgFile, flags=1)  # flags=1 读取彩色图像(BGR)
    img2 = cv2.imread(imgFile, flags=0)  # flags=0 读取为灰度图像

# 1.10 图像显示(plt.imshow)
    imgRGB = cv2.cvtColor(img1, cv2.COLOR_BGR2RGB)  # 图片格式转换：BGR(OpenCV) -> RGB(PyQt5)
    imGray = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)  # 图片格式转换：BGR(OpenCV) -> Gray    

进一步地，通过函数 cv2.threshold 可以对图像进行二值化处理。

函数说明：

cv2.threshold(src, thresh, maxval, type[, dst]) → retval, dst

函数 threshold() 可以将灰度图像转换为二值图像，图像完全由像素 0 和 255 构成，呈现出只有黑白两色的视觉效果。

灰度阈值化通过选取的灰度阈值 thresh，将每个像素的灰度值与阈值进行比较，将灰度大于阈值的像素点置为最大灰度，小于阈值的像素点置为最小灰度，得到二值图像，可以突出图像轮廓，把目标从背景中分割出来。

参数说明：

• scr：变换操作的输入图像，nparray 二维数组，必须是单通道灰度图像！
• thresh：阈值，取值范围 0~255
• maxval：填充色，取值范围 0～255，一般取 255
• type：变换类型
  • cv2.THRESH_BINARY：大于阈值时置 255，否则置 0
  • cv2.THRESH_BINARY_INV：大于阈值时置 0，否则置 255
  • cv2.THRESH_TRUNC：大于阈值时置为阈值 thresh，否则不变（保持原色）
  • cv2.THRESH_TOZERO：大于阈值时不变（保持原色），否则置 0
  • cv2.THRESH_TOZERO_INV：大于阈值时置 0，否则不变（保持原色）
  • cv2.THRESH_OTSU：使用 OTSU 算法选择阈值
• 返回值 retval：返回二值化的阈值
• 返回值 dst：返回阈值变换的输出图像

注意：

• 1. 函数 cv2.threshold 进行固定阈值的二值化处理；函数 cv2.adaptiveThreshold 为自适应阈值的二值化处理函数，可以通过比较像素点与周围像素点的关系动态调整阈值。
• 2. 确切地说，只有 type 为 cv2.THRESH_BINARY 或 cv2.THRESH_BINARY_INV 时输出为二值图像，其它变换类型时进行阈值处理但并不是二值处理。

例程：1.47 图像的二值变换（固定阈值）

    # 1.47 固定阈值二值变换
    img = cv2.imread("../images/imgLena.tif")  # 读取彩色图像(BGR)
    imgGray = cv2.imread("../images/imgLena.tif", flags=0)  # flags=0 读取为灰度图像
    # imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 颜色转换：BGR(OpenCV) -> Gray

    # cv2.threshold(src, thresh, maxval, type[, dst]) → retval, dst
    ret1, img1 = cv2.threshold(imgGray, 63, 255, cv2.THRESH_BINARY)  # 转换为二值图像, thresh=63
    ret2, img2 = cv2.threshold(imgGray, 127, 255, cv2.THRESH_BINARY)  # 转换为二值图像, thresh=127
    ret3, img3 = cv2.threshold(imgGray, 191, 255, cv2.THRESH_BINARY)  # 转换为二值图像, thresh=191
    ret4, img4 = cv2.threshold(imgGray, 127, 255, cv2.THRESH_BINARY_INV)  # 逆二值图像，BINARY_INV
    ret5, img5 = cv2.threshold(imgGray, 127, 255, cv2.THRESH_TRUNC)  # TRUNC 阈值处理，THRESH_TRUNC
    ret6, img6 = cv2.threshold(imgGray, 127, 255, cv2.THRESH_TOZERO)  # TOZERO 阈值处理，THRESH_TOZERO

    plt.figure(figsize=(9, 6))
    titleList = ["1. BINARY(thresh=63)", "2. BINARY(thresh=127)", "3. BINARY(thresh=191)", "4. THRESH_BINARY_INV", "5. THRESH_TRUNC", "6. THRESH_TOZERO"]
    imageList = [img1, img2, img3, img4, img5, img6]
    for i in range(6):
        plt.subplot(2, 3, i+1), plt.title(titleList[i]), plt.axis('off')
        plt.imshow(imageList[i], 'gray')  # 灰度图像 ndim=2
    plt.show()

---

3. 图像的灰度变换

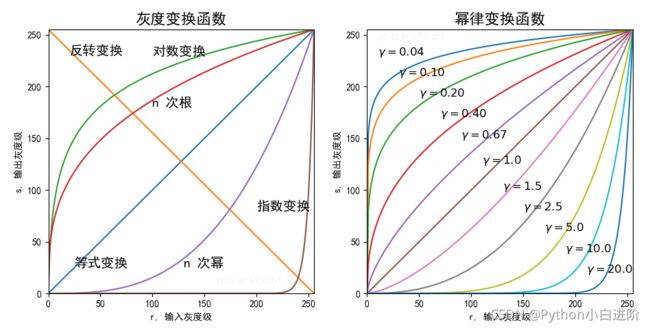
灰度变换是图像增强的重要方法，可以使图像动态范围扩大、图像对比度增强，图像更清晰，特征更明显，从而改善图像的显示效果。

灰度变换就是按一定规则（灰度映射函数）修改图像每一个像素的灰度值，从而改变图像灰度的动态范围。按照灰度映射函数的性质，灰度变换可以分为线性变换、分段线性和非线性变换，非线性变换中对数变换、指数变换和幂律变换（n次幂、n次根）最为常用。常见的灰度变换函数的形状如下图所示。

3.1 反色变换（图像反转）

图像的反色变换，即图像反转，将黑色像素点变白色，白色像素点变黑色。广义的反色变换也可以应用于彩色图像，即对所有像素点取补。

图像的反转处理可以增强暗色区域中的白色或灰色细节。

注意图像反转（Invert）与图像翻转（Flip）的区别：图像翻转是沿对称轴的几何变换，像素值不变；图像反转是像素颜色的逆转，像素位置不变。

例程：1.48 图像的反色变换

    # 1.48 图像的反色变换
    img = cv2.imread("../images/imgLena.tif")  # 读取彩色图像(BGR)
    imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 颜色转换：BGR(OpenCV) -> Gray
    h, w = img.shape[:2]  # 图片的高度和宽度

    # imgInv = np.zeros_like(img)  # 创建与 img 相同形状的黑色图像
    imgInv = np.empty((w, h), np.uint8)  # 创建空白数组
    for i in range(h):
        for j in range(w):
            imgInv[i][j] = 255 - imgGray[i][j]

    plt.figure(figsize=(10,6))
    plt.subplot(131), plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB)), plt.title("imgBGR"), plt.axis('off')
    plt.subplot(132), plt.imshow(imgGray, cmap='gray'), plt.title("imgGray"), plt.axis('off')
    plt.subplot(133), plt.imshow(imgInv, cmap='gray'), plt.title("imgInv"), plt.axis('off')
    plt.show()

3.2 线性灰度变换

线性灰度变换将原始图像灰度值的动态范围按线性关系扩展到指定范围或整个动态范围。

线性灰度变化对图像的每一个像素作线性拉伸，可以凸显图像的细节，提高图像的对比度。

线性灰度变换可以由以下公式描述 ：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Dt &= \frac{d-…
式中，D 为原始图像的灰度值，Dt 为线性灰度变换后的图像灰度值。

• 当 $\alpha =1，\beta =0$ 时，保持原始图像不变
• 当 $\alpha =1，\beta >0$ 时，图像的灰度值上移，灰度图像颜色发白（彩色图像颜色发亮）
• 当 $\alpha =1，\beta <0$ 时，图像的灰度值下移，灰度图像颜色发黑（彩色图像颜色发暗）
• 当 $\alpha >1$ 时，图像的对比度增强
• 当 $0<\alpha <1$ 时，图像的对比度减小
• 当 $\alpha <0，\beta =255$ 时，图像暗区域变亮，亮区域变暗，图像求补
• 当 $\alpha =-1，\beta =255$ 时，图像的灰度值反转

直方图正规化是根据图像的最小灰度级和最大灰度级，将其拉伸到灰度级全域 [0,255] 的线性变换。

例程：1.49 图像的线性灰度变换

    # 1.49 图像的线性灰度变换
    img = cv2.imread("../images/imgLena.tif")  # 读取彩色图像(BGR)
    imgGray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)  # 颜色转换：BGR(OpenCV) -> Gray
    h, w = img.shape[:2]  # 图片的高度和宽度
    img1 = np.empty((w, h), np.uint8)  # 创建空白数组
    img2 = np.empty((w, h), np.uint8)  # 创建空白数组
    img3 = np.empty((w, h), np.uint8)  # 创建空白数组
    img4 = np.empty((w, h), np.uint8)  # 创建空白数组
    img5 = np.empty((w, h), np.uint8)  # 创建空白数组
    img6 = np.empty((w, h), np.uint8)  # 创建空白数组

    # Dt[i,j] = alfa*D[i,j] + beta
    alfa1, beta1 = 1, 50  # alfa=1,beta>0: 灰度值上移
    alfa2, beta2 = 1, -50  # alfa=1,beta<0: 灰度值下移
    alfa3, beta3 = 1.5, 0  # alfa>1,beta=0: 对比度增强
    alfa4, beta4 = 0.75, 0  # 0
    alfa5, beta5 = -0.5, 0  # alfa<0,beta=0: 暗区域变亮，亮区域变暗
    alfa6, beta6 = -1, 255  # alfa=-1,beta=255: 灰度值反转

    for i in range(h):
        for j in range(w):
            img1[i][j] = min(255, max((imgGray[i][j]+beta1), 0))  # alfa=1,beta>0: 颜色发白
            img2[i][j] = min(255, max((imgGray[i][j]+beta2), 0))  # alfa=1,beta<0: 颜色发黑
            img3[i][j] = min(255, max(alfa3*imgGray[i][j], 0))  # alfa>1,beta=0: 对比度增强
            img4[i][j] = min(255, max(alfa4*imgGray[i][j], 0))  # 0
            img5[i][j] = alfa5*imgGray[i][j]+beta5  # alfa<0,beta=255: 暗区域变亮，亮区域变暗
            img6[i][j] = min(255, max(alfa6*imgGray[i][j]+beta6, 0))  # alfa=-1,beta=255: 灰度值反转

    plt.figure(figsize=(10, 6))
    titleList = ["1. imgGray", "2. beta=50", "3. beta=-50", "4. alfa=1.5", "5. alfa=0.75", "6. alfa=-0.5"]
    imageList = [imgGray, img1, img2, img3, img4, img5]
    for i in range(6):
        plt.subplot(2, 3, i + 1), plt.title(titleList[i]), plt.axis('off')
        plt.imshow(imageList[i], vmin=0, vmax=255, cmap='gray')
    plt.show()

3.3 分段线性灰度变换

分段线性变换函数可以增强图像各部分的反差，增强感兴趣的灰度区间、抑制不感兴趣的灰度级。

分段线性函数的优点是可以根据需要拉伸特征物的灰度细节，一些重要的变换只能用分段函数来描述和实现，缺点则是参数较多不容易确定。

分段线性函数通用公式如下：
$$Dt=\{\begin{array}{ll}\frac{c}{a}D& ,0\le D<a\\ \frac{d-c}{b-a}[D-a]+c& ,a\le D\le b\\ \frac{f-d}{e-b}[D-a]+d& ,b<D\le e\end{array}$$
式中，D 为原始图像的灰度值，Dt 为线性灰度变换后的图像灰度值。

例程：1.50 分段线性灰度变换（对比度拉伸）

对比度拉伸可以扩展图像中的灰度级范围，从而覆盖设备的理想灰度范围。

对比度拉伸变换函数可以有不同的实现方案，如将原始灰度范围拉伸到较宽的灰度范围；或将原始灰度范围拉伸到全域灰度范围（0，255）；或将原始灰度范围拉伸到较宽的灰度范围，同时对下限或上限进行截断处理。

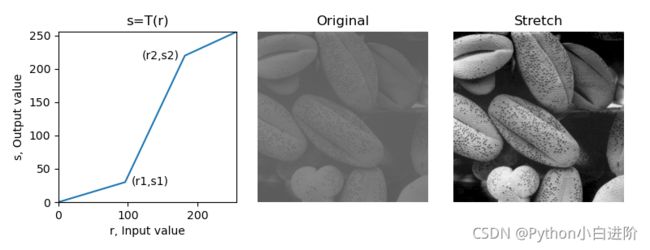
本例程令 (r1, s1) = (rMin, 0)、(r2, s2) = (rmax, L-1)，其中 rMin、rMax 表示图像中最小灰度值和最大灰度值，将原始图像的灰度级分段线性拉伸到整个范围 [0, L-1]。运行结果的左图显示本例程的拉伸变换曲线。

    # 1.50 分段线性灰度变换 (对比度拉伸)
    imgGray = cv2.imread("../images/Fig0310b.tif", flags=0)  # flags=0 读取为灰度图像
    height, width = imgGray.shape[:2]  # 图片的高度和宽度

    # constrast stretch, (r1,s1)=(rMin,0), (r2,s2)=(rMax,255)
    rMin = imgGray.min()  # 原始图像灰度的最小值
    rMax = imgGray.max()  # 原始图像灰度的最大值
    r1, s1 = rMin, 0  # (x1,y1)
    r2, s2 = rMax, 255  # (x2,y2)

    imgStretch = np.empty((width, height), np.uint8)  # 创建空白数组
    k1 = s1 / r1  # imgGray[h,w] < r1:
    k2 = (s2-s1) / (r2-r1)  # r1 <= imgGray[h,w] <= r2
    k3 = (255-s2) / (255-r2)  # imgGray[h,w] > r2
    for h in range(height):
        for w in range(width):
            if imgGray[h,w] < r1:
                imgStretch[h,w] = k1 * imgGray[h,w]
            elif r1 <= imgGray[h,w] <= r2:
                imgStretch[h,w] = k2 * (imgGray[h,w] - r1) + s1
            elif imgGray[h,w] > r2:
                imgStretch[h,w] = k3 * (imgGray[h,w] - r2) + s2

    plt.figure(figsize=(10,3.5))
    plt.subplots_adjust(left=0.2, bottom=0.2, right=0.9, top=0.8, wspace=0.1, hspace=0.1)
    plt.subplot(131), plt.title("s=T(r)")
    x = [0, 96, 182, 255]
    y = [0, 30, 220, 255]
    plt.plot(x, y)
    plt.axis([0,256,0,256])
    plt.text(105, 25, "(r1,s1)", fontsize=10)
    plt.text(120, 215, "(r2,s2)", fontsize=10)
    plt.xlabel("r, Input value")
    plt.ylabel("s, Output value")
    plt.subplot(132), plt.imshow(imgGray, cmap='gray', vmin=0, vmax=255), plt.title("Original"), plt.axis('off')
    plt.subplot(133), plt.imshow(imgStretch, cmap='gray', vmin=0, vmax=255), plt.title("Stretch"), plt.axis('off')
    plt.show()

例程：1.53 分段线性灰度变换（灰度级分层）

灰度级分层可以突出图像中特定的灰度级区间，可以对灰度级进行分层处理。

灰度级分层有两种常用方案：一种方案是二值处理，将感兴趣的灰度级区间设为较大的灰度值，其它区间设为较小的灰度值；另一种方案是窗口处理，将感兴趣的灰度级区间设为较大的灰度值，其它区间不变。

两种灰度级分层方案的分段变换公式分别为：
$$\begin{gathered} D{t}_1=\{\begin{array}{ll}d& ,a\le D\le b\\ c& ,else\end{array} \\ D{t}_2=\{\begin{array}{ll}d& ,a\le D\le b\\ D& ,else\end{array} \end{gathered}$$
式中，D 为原始图像的灰度值，Dt1、Dt2 为灰度变换后的图像灰度值。

例程 1.53 对于肾部区域主动脉血管造影图像，采用灰度级分层技术增强主要血管，将感兴趣的灰度级区间显示为白色。方案一进行二值化处理，将其它灰度区间设为黑色；方案二则保留其它灰度区间的灰度值不变。

    # # 1.53 分段线性灰度变换 (灰度级分层)  # Gray layered
    imgGray = cv2.imread("../images/Fig0312a.tif", flags=0)  # flags=0 读取为灰度图像
    width, height = imgGray.shape[:2]  # 图片的高度和宽度

    # Gray layered strategy 1: binary image
    a, b = 155, 245  # 突出 [a, b] 区间的灰度
    imgLayer1 = imgGray.copy()
    imgLayer1[(imgLayer1[:,:]b)] = 0  # 其它区域：黑色
    imgLayer1[(imgLayer1[:,:]>=a) & (imgLayer1[:,:]<=b)] = 255  # 灰度级窗口：白色

    # Gray layered strategy 2: grayscale image
    imgLayer2 = imgGray.copy()
    imgLayer2[(imgLayer2[:,:]>=a) & (imgLayer2[:,:]<=b)] = 255  # 灰度级窗口：白色，其它区域不变

    plt.figure(figsize=(10, 6))
    plt.subplot(131), plt.imshow(imgGray, cmap='gray'), plt.title('Original'), plt.axis('off')
    plt.subplot(132), plt.imshow(imgLayer1, cmap='gray'), plt.title('Binary layered'), plt.axis('off')
    plt.subplot(133), plt.imshow(imgLayer2, cmap='gray'), plt.title('Grayscale layered'), plt.axis('off')
    plt.show()

例程：1.54 分段线性灰度变换（比特平面分层）

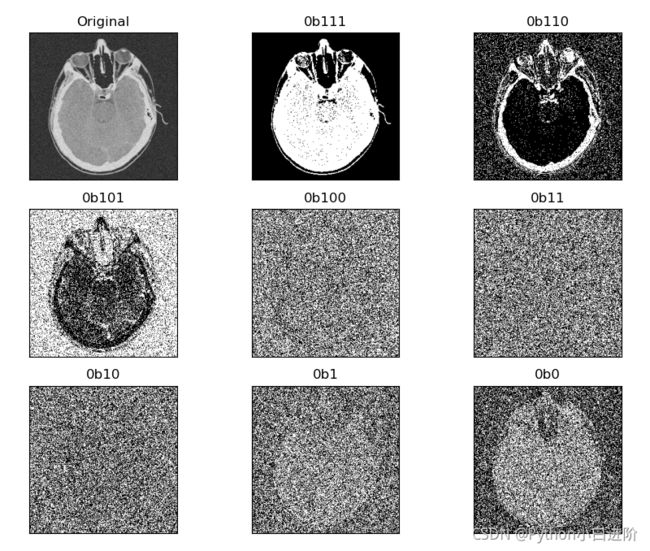
像素值也可以表示为二进制形式，对 8bits 二进制数的每一位进行切片，可以得到 8 个比特平面，称为比特平面分层（Bit-plane slicing）。
通常，高阶比特平面包含了大量有视觉意义的数据，而低阶比特平面包含了更精细的灰度细节。因此，比特平面分层可以用于图像压缩和图像重建。

    # # 1.54 分段线性灰度变换 (比特平面分层)  Bit-plane slicing
    img = cv2.imread("../images/Fig0726a.tif", flags=0)  # flags=0 读取为灰度图像
    height, width = img.shape[:2]  # 图片的高度和宽度
    # imgRec = np.zeros((height, width), dtype=np.uint8)  # 创建零数组

    plt.figure(figsize=(10, 8))
    for l in range(9, 0, -1):
        plt.subplot(3, 3, (9-l)+1, xticks=[], yticks=[])
        if l==9:
            plt.imshow(img, cmap='gray'), plt.title('Original')
        else:
            imgBit = np.empty((height, width), dtype=np.uint8)  # 创建空数组
            for w in range(width):
                for h in range(height):
                    x = np.binary_repr(img[w,h], width=8)  # 以字符串形式返回输入数字的二进制表示形式
                    x = x[::-1]
                    a = x[l-1]
                    imgBit[w,h] = int(a)  # 第 i 位二进制的值
            plt.imshow(imgBit, cmap='gray')
            plt.title(f"{bin((l-1))}")
    plt.show()

---

3.4 非线性灰度变换：对数变换和指数变换

对数变换可以由以下公式描述：
$$Dt=c\ast log(1+D)$$
对数曲线在像素值较低的区域斜率大，在像素值较高的区域斜率小。对数变换将输入中范围较窄的低灰度值映射为范围较宽的灰度级，输入中的高灰度值则被映射为范围较窄的灰度级。对数变换后，较暗区域的对比度提升，可以增强图像的暗部细节。

对数变换实现了扩展低灰度值而压缩高灰度值的效果，广泛应用于频谱图像的显示中。对数变换的典型应用是傅立叶频谱的动态范围很宽，直接显示时受显示设备动态范围的限制而丢失大量的暗部细节；使用对数变换将图像的动态范围进行非线性压缩后，就可以清晰地显示。

例程：1.55 图像的对数变换

    # 1.55 图像的非线性灰度变换：对数变换
    img = cv2.imread("../images/Fig0305a.tif", flags=0)  # flags=0 读取为灰度图像

    normImg = lambda x: 255. * (x-x.min()) / (x.max()-x.min()+1e-6)  # 归一化
    fft = np.fft.fft2(img)  # 傅里叶变换
    fft_shift = np.fft.fftshift(fft)  # 中心化
    amp = np.abs(fft_shift)  # 傅里叶变换的频谱
    amp = np.uint8(normImg(amp))  # 映射到 [0, 255]
    ampLog = np.abs(np.log(1 + np.abs(fft_shift)))  # 对数变换
    ampLog = np.uint8(normImg(ampLog))  # 映射到 [0, 255]

    plt.figure(figsize=(9, 5))
    plt.subplot(131), plt.imshow(img, cmap='gray', vmin=0, vmax=255), plt.title('Original'), plt.axis('off')
    plt.subplot(132), plt.imshow(amp, cmap='gray', vmin=0, vmax=255), plt.title("FFT spectrum"), plt.axis('off')
    plt.subplot(133), plt.imshow(ampLog, cmap='gray', vmin=0, vmax=255), plt.title("FFT spectrum - log trans"), plt.axis('off')
    plt.tight_layout()
    plt.show()

3.5 非线性灰度变换：幂律变换（伽马变换）

幂律变换也称伽马变换，可以提升暗部细节，对发白（曝光过度）或过暗（曝光不足）的图片进行矫正。

幂律变换可以由以下公式描述：
$$Dt=c\ast (D+ϵ{)}^{\gamma }$$
伽马变换本质上是对图像矩阵中的每个值进行幂运算。$ 0< \gamma <1$ 时，拉伸图像中灰度级较低的区域，压缩灰度级较高的部分，增加图像的对比度；$\gamma >1$ 时，拉伸图像中灰度级较高的区域，压缩灰度级较低的部分，降低图像的对比度。
伽马变换通过非线性变换对人类视觉特性进行补偿，最大化地利用有效的灰度级带宽。很多拍摄、显示、打印设备的亮度曲线都符合幂律曲线，因此伽马变换广泛应用于各种设备显示效果的调校，称为伽马校正。

例程：1.56 图像的幂律变换

    # 1.56 图像的非线性灰度变换: 幂律变换 (伽马变换)
    img = cv2.imread("../images/imgB2.jpg", flags=0)  # flags=0 读取为灰度图像

    gammaList = [0.125, 0.25, 0.5, 1.0, 2.0, 4.0]  # gamma 值
    normImg = lambda x: 255. * (x-x.min()) / (x.max()-x.min()+1e-6)  # 归一化为 [0,255]

    plt.figure(figsize=(9,6))
    for k in range(len(gammaList)):
        imgGamma = np.power(img, gammaList[k])
        imgGamma = np.uint8(normImg(imgGamma))

        plt.subplot(2, 3, k+1), plt.axis('off')
        plt.imshow(imgGamma,  cmap='gray', vmin=0, vmax=255)
        plt.title(f"$\gamma={
       gammaList[k]}$")
    plt.show()

---

4. 图像的直方图处理

4.1 灰度直方图

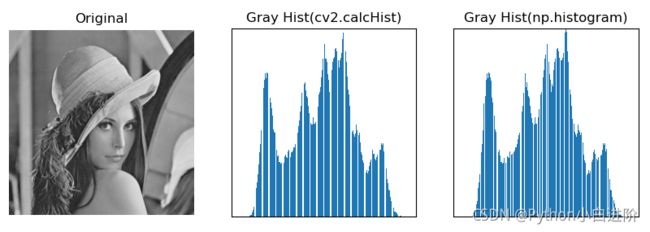
图像直方图是反映图像像素分布的统计表，横坐标代表像素值的取值区间，纵坐标代表每一像素值在图像中的像素总数或者所占的百分比。 灰度直方图是图像灰度级的函数，用来描述每个灰度级在图像矩阵中的像素个数。

灰度直方图反映了图像中的灰度分布规律，直观地表现了图像中各灰度级的占比，很好地体现出图像的亮度和对比度信息：灰度图分布居中说明亮度正常，偏左说明亮度较暗，偏右表明亮度较高；狭窄陡峭表明对比度降低，宽泛平缓表明对比度较高。

根据直方图的形态可以判断图像的质量，通过调控直方图的形态可以改善图像的质量。

OpenCV 提供了函数 cv2.calcHist 可以计算直方图，Numpy 中的函数 np.bincount 也可以实现同样的功能。

函数说明：

cv2.calcHist(images, channels, mask, histSize, ranges[, hist[, accumulate ]]) → hist

函数 cv2.calcHist 可以计算一维直方图或二维直方图，函数的参数 images, channels, histSize, ranges 在计算一维直方图时也要带 [] 号。

参数说明：

• images：输入图像，用 [] 括号表示
• channels： 直方图计算的通道，用 [] 括号表示
• mask：掩模图像，一般置为 None
• histSize：直方柱的数量，一般取 256
• ranges：像素值的取值范围，一般为 [0,256]
• 返回值 hist：返回每一像素值在图像中的像素总数，形状为 (histSize,1)

注意：

• 1. 参数 images, channels, histSize, ranges 都要带 [] 号。
• 2. mask 是与 images 大小相同的掩模图像，掩模为 0 的区域不作处理。不使用掩模时设为 None。
     3. channels 设置对彩色图像的指定通道计算直方图，灰度图像时设为 0。
     4. Numpy 中的函数 np.bincount 也可以实现同样的功能，但该函数返回值的形状为 (histSize,)

例程：1.57 图像的灰度直方图

    # 1.57 图像的灰度直方图
    img = cv2.imread("../images/imgLena.tif", flags=0)  # flags=0 读取为灰度图像

    histCV = cv2.calcHist([img], [0], None, [256], [0, 256])  # OpenCV 函数 cv2.calcHist
    histNP, bins = np.histogram(img.flatten(), 256)
    print(histCV.shape, histNP.shape)  # histCV: (256, 1), histNP: (256,)

    plt.figure(figsize=(10,3))
    plt.subplot(131), plt.imshow(img, cmap='gray', vmin=0, vmax=255), plt.title("Original"), plt.axis('off')
    plt.subplot(132,xticks=[], yticks=[]), plt.axis([0,255,0,np.max(histCV)])
    plt.bar(range(256), histCV[:,0]), plt.title("Gray Hist(cv2.calcHist)")
    plt.subplot(133,xticks=[], yticks=[]), plt.axis([0,255,0,np.max(histCV)])
    plt.bar(bins[:-1], histNP), plt.title("Gray Hist(np.histogram)")
    plt.show()

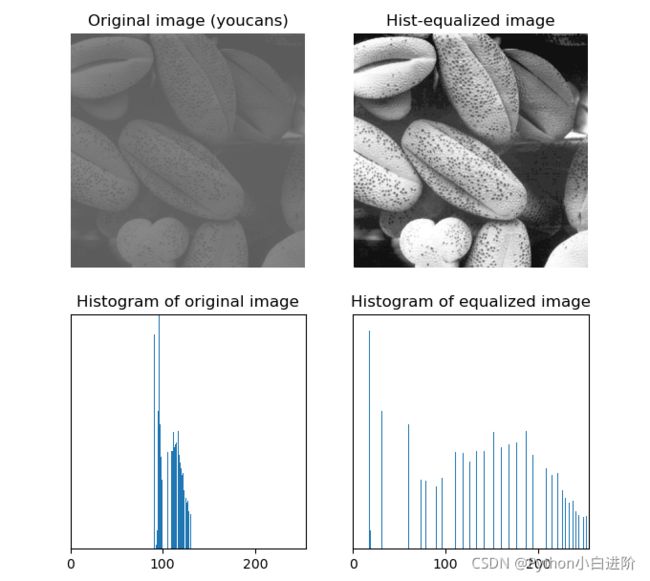
4.2 直方图均衡化

直方图均衡化是一种简单有效的图像增强技术。根据直方图的形态可以判断图像的质量，通过调控直方图的形态可以改善图像的质量。

直方图均衡化是将原始图像通过函数变换，调控图像的灰度分布，得到直方图分布合理的新图像，以此来调节图像亮度、增强动态范围偏小的图像的对比度。

由于人眼视觉特性，直方图均匀分布的图像视觉效果较好。直方图均衡化的基本思想是对图像中占比大的灰度级进行展宽，而对占比小的灰度级进行压缩，使图像的直方图分布较为均匀，扩大灰度值差别的动态范围，从而增强图像整体的对比度。

因此，直方图均衡化就是对图像进行非线性拉伸，重新分配图像像素值，本质上是根据直方图对图像进行线性或非线性灰度变换。

例如，直方图均衡化可以把原始图像的直方图调整到均匀分布，增加像素之间灰度值差别的动态范围，从而增强图像整体的对比度。

通过累积分布函数（cumulative distribution function, CDF）可以实现将原图像 r 的分布转换成 s 的均匀分布，累计分布函数（CDF）就是是概率密度函数（probability density function, PDF）的积分。

若 $p_r(r)$ 和 $p_s(s) $表示原图像 r 和新图像 s 的概率密度函数，则：
$$s=T(r)=(L-1){\int }_0^r{p}_r(r)dr$$
其离散形式为：
$$s_k=T(r_k)=(L-1)\sum _{j=0}^k{p}_r(r_j)=(L-1)\sum _{j=0}^k\frac{n_j}{N}$$
于是，可以通过原图像的直方图直接求出均衡化后各像素的灰度级 $s_k$，得到实现直方图均衡的转换函数：

（1）计算原始灰度图像的直方图；

（2）通过直方图累加计算原始图像的累计分布函数 CDF；

（3）基于累计分布函数 CDF，通过插值计算得到新的灰度值。

OpenCV 提供了函数 cv2. equalizeHist 可以实现直方图均衡化。

函数说明：

cv2.qualizeHist(src[, dst]) → dst

参数说明：

• src：输入图像
• 返回值 dst：输出图像，直方图均衡化

例程：1.58 直方图均衡

    # 1.58 直方图均衡
    img = cv2.imread("../images/Fig0310b.tif", flags=0)  # flags=0 读取为灰度图像

    imgEqu = cv2.equalizeHist(img)  # 使用 cv2.qualizeHist 完成直方图均衡化变换

    # histogram equalization image
    # histImg, bins = np.histogram(img.flatten(), 256)  # 计算原始图像直方图
    # cdf = histImg.cumsum()  # 计算累积分布函数 CDF
    # cdf = cdf * 255 / cdf[-1]  # 累计函数 CDF 归一化: [0,1]->[0,255]
    # imgEqu = np.interp(img.flatten(), bins[:256], cdf)  # 线性插值，计算新的灰度值
    # imgEqu = imgEqu.reshape(img.shape)  # 将压平的图像数组重新变成二维数组

    fig = plt.figure(figsize=(7,7))
    plt.subplot(221), plt.title("Original image (youcans)"), plt.axis('off')
    plt.imshow(img, cmap='gray', vmin=0, vmax=255)  # 原始图像
    plt.subplot(222),plt.title("Hist-equalized image"), plt.axis('off')
    plt.imshow(imgEqu, cmap='gray', vmin=0, vmax=255)  # 转换图像
    histImg, bins = np.histogram(img.flatten(), 256)  # 计算原始图像直方图
    plt.subplot(223, yticks=[]), plt.bar(bins[:-1], histImg)  # 原始图像直方图
    plt.title("Histogram of original image"), plt.axis([0,255,0,np.max(histImg)])
    histEqu, bins = np.histogram(imgEqu.flatten(), 256)  # 计算原始图像直方图
    plt.subplot(224, yticks=[]), plt.bar(bins[:-1], histEqu)  # 转换图像直方图
    plt.title("Histogram of equalized image"), plt.axis([0,255,0,np.max(histImg)])
    plt.show()

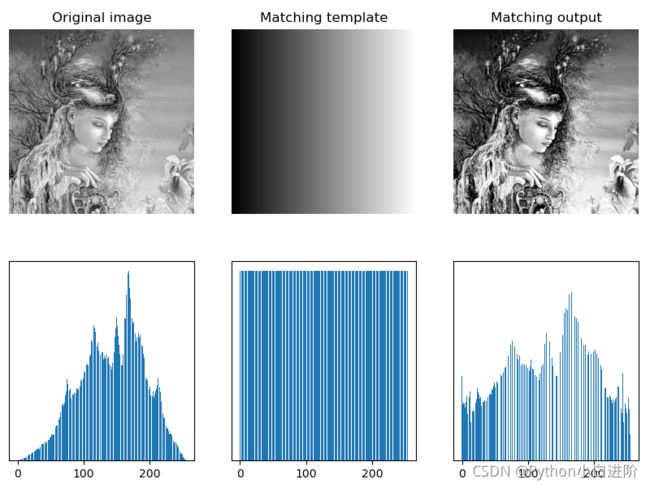
4.3 直方图匹配

直方图均衡直接对图像全局进行均衡化，生成具有均匀直方图的图像，并不考虑局部图像区域的具体情况。对于一幅图像的局部区域、具体缺陷，有时需要生成具有特殊形状直方图的图像。

直方图匹配又称为直方图规定化，是指将图像的直方图调整为规定的形状。 例如，将一幅图像或某一区域的直方图匹配到另一幅影像上，使两幅影像的色调保持一致。

这就需要在直方图均衡的基础上，再进行一次反变换，将均匀形状的直方图调整为规定的形状。

直方图匹配的主要步骤为：

（1）通过规定图像 z 的直方图 $p_z(z)$，计算其直方图均衡变换的 $s_k$；

（2）通过 $s_k$ 计算图像 z 的直方图均衡变换函数 $G$，$G(z_q)=s_k$；

（3）计算变换函数 $G$ 的逆变换函数 $G^{-1}$，$z_q=G^{-1}(s_k)$；

（4）对输入图像 r 进行直方图均衡得到均衡图像 s，然后再用逆变换函数 $G^{-1}$ 将其映射到 $p_z(z)$，得到直方图匹配图像 z。本步骤中的两次变换，也可以合并为一次完成。

例程：1.59 灰度图像直方图匹配

    # 1.59 灰度图像直方图匹配
    img = cv2.imread("../images/imgGaia.tif", flags=0)  # flags=0 读取为灰度图像
    imgRef = cv2.imread("../images/Fig0307a.tif", flags=0)  # 匹配模板图像, matching template

    # imgOut = calcHistMatch(img, imgRef)  # 子程序：直方图匹配

    # 计算累计直方图
    histImg, bins = np.histogram(img.flatten(), 256)  # 计算原始图像直方图
    histRef, bins = np.histogram(imgRef.flatten(), 256)  # 计算匹配模板直方图
    cdfImg = histImg.cumsum()  # 计算原始图像累积分布函数 CDF
    cdfRef = histRef.cumsum()  # 计算匹配模板累积分布函数 CDF

    # 计算直方图匹配转换函数
    transM = np.zeros(256)
    for i in range(256):
        index = 0
        vMin = np.fabs(cdfImg[i] - cdfRef[0])
        for j in range(256):
            diff = np.fabs(cdfImg[i] - cdfRef[j])
            if (diff < vMin):
                index = int(j)
                vMin = diff
        transM[i] = index

    # 直方图匹配
    # imgOut = np.zeros_like(img)
    imgOut = transM[img].astype(np.uint8)

    fig = plt.figure(figsize=(10,7))
    plt.subplot(231), plt.title("Original image"), plt.axis('off')
    plt.imshow(img, cmap='gray')  # 原始图像
    plt.subplot(232), plt.title("Matching template"), plt.axis('off')
    plt.imshow(imgRef, cmap='gray')  # 匹配模板
    plt.subplot(233), plt.title("Matching output"), plt.axis('off')
    plt.imshow(imgOut, cmap='gray')  # 匹配结果
    histImg, bins = np.histogram(img.flatten(), 256)  # 计算原始图像直方图
    plt.subplot(234, yticks=[]), plt.bar(bins[:-1], histImg)
    histRef, bins = np.histogram(imgRef.flatten(), 256)  # 计算匹配模板直方图
    plt.subplot(235, yticks=[]), plt.bar(bins[:-1], histRef)
    histOut, bins = np.histogram(imgOut.flatten(), 256)  # 计算匹配结果直方图
    plt.subplot(236, yticks=[]), plt.bar(bins[:-1], histOut)
    plt.show()

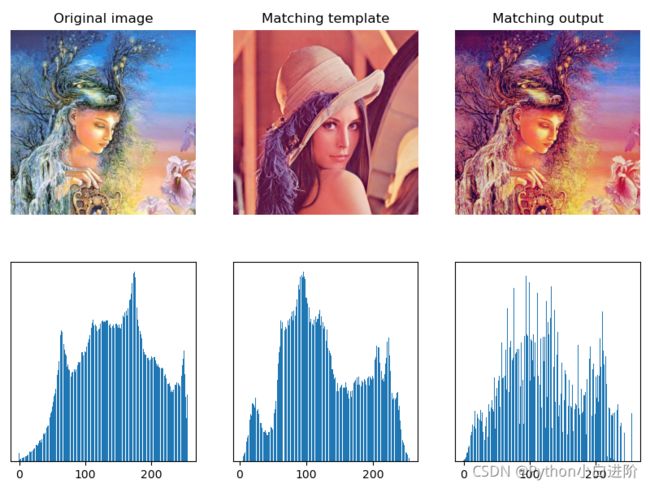
例程：1.60 彩色图像直方图匹配

    # 1.60 彩色图像的直方图匹配

    img = cv2.imread("../images/imgGaia.tif", flags=1)  # flags=1 读取为彩色图像
    imgRef = cv2.imread("../images/imgLena.tif", flags=1)  # 匹配模板图像 (matching template)

    _, _, channel = img.shape
    imgOut = np.zeros_like(img)
    for i in range(channel):
        print(i)
        histImg, _ = np.histogram(img[:,:,i], 256)  # 计算原始图像直方图
        histRef, _ = np.histogram(imgRef[:,:,i], 256)  # 计算匹配模板直方图
        cdfImg = np.cumsum(histImg)  # 计算原始图像累积分布函数 CDF
        cdfRef = np.cumsum(histRef)  # 计算匹配模板累积分布函数 CDF
        for j in range(256):
            tmp = abs(cdfImg[j] - cdfRef)
            tmp = tmp.tolist()
            index = tmp.index(min(tmp))  # find the smallest number in tmp, get the index of this number
            imgOut[:,:,i][img[:,:,i]==j] = index

    fig = plt.figure(figsize=(10,7))
    plt.subplot(231), plt.title("Original image"), plt.axis('off')
    plt.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB))  # 显示原始图像
    plt.subplot(232), plt.title("Matching template"), plt.axis('off')
    plt.imshow(cv2.cvtColor(imgRef, cv2.COLOR_BGR2RGB))  # 显示匹配模板
    plt.subplot(233), plt.title("Matching output"), plt.axis('off')
    plt.imshow(cv2.cvtColor(imgOut, cv2.COLOR_BGR2RGB))  # 显示匹配结果
    histImg, bins = np.histogram(img.flatten(), 256)  # 计算原始图像直方图
    plt.subplot(234, yticks=[]), plt.bar(bins[:-1], histImg)
    histRef, bins = np.histogram(imgRef.flatten(), 256)  # 计算匹配模板直方图
    plt.subplot(235, yticks=[]), plt.bar(bins[:-1], histRef)
    histOut, bins = np.histogram(imgOut.flatten(), 256)  # 计算匹配结果直方图
    plt.subplot(236, yticks=[]), plt.bar(bins[:-1], histOut)
    plt.show()

4.4 局部直方图处理

直方图均衡和直方图匹配都是基于整幅图像的灰度分布进行全局变换，并非针对图像局部区域的细节进行增强。

直方图处理对于局部同样适用，局部直方图处理的思想是基于像素邻域的灰度分布进行直方图变换处理。

局部直方图处理的过程是：

（1）设定某一大小的模板（矩形邻域），在图像中沿逐个像素移动；

（2）对每个像素位置，计算模板区域的直方图，对该局部区域进行直方图均衡或直方图匹配变换，变换结果只用于模板区域中心像素点的灰度值修正；

（3）模板（邻域）在图像中逐行逐列移动，遍历所有像素点，完成对整幅图像的局部直方图处理。

OpenCV 提供了类 cv2. createCLAHE 用于创建自适应均衡化的对象和方法，可以实现局部直方图处理。

函数说明：

cv2.createCLAHE([, clipLimit[, tileGridSize]]) → retval

参数说明：

• clipLimit：颜色对比度的阈值，可选项，默认值 8
• titleGridSize：局部直方图均衡化的模板（邻域）大小，可选项，默认值 (8,8)

cv2. createCLAHE 是一种限制对比度自适应直方图均衡化方法（Contrast Limited Adaptive Hitogram Equalization），采用了限制直方图分布的方法和加速的插值方法。

基本例程：1.61 自适应的局部直方图均衡

    # 1.61 局部直方图均衡化
    img = cv2.imread("../images/FigClahe.jpg", flags=0)  # flags=0 读取为灰度图像

    imgEqu = cv2.equalizeHist(img)  # 全局直方图均衡化
    clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(4,4))  # 创建 CLAHE 对象
    imgLocalEqu = clahe.apply(img)  # 自适应的局部直方图均衡化

    plt.figure(figsize=(9, 6))
    plt.subplot(131), plt.title('Original'), plt.axis('off')
    plt.imshow(img, cmap='gray', vmin=0, vmax=255)
    plt.subplot(132), plt.title(f'Global Equalize Hist'), plt.axis('off')
    plt.imshow(imgEqu, cmap='gray', vmin=0, vmax=255)
    plt.subplot(133), plt.title(f'Local Equalize Hist'), plt.axis('off')
    plt.imshow(imgLocalEqu, cmap='gray', vmin=0, vmax=255)
    plt.tight_layout()
    plt.show()

4.5 直方图统计量图像增强

直方图统计量图像增强，是基于直方图的统计量信息（如均值和方差）对图像的灰度和对比度进行调整。直方图统计量不仅用于图像的全局增强，在图像局部增强中更加有效。

局部均值和方差是根据像素邻域特征进行灰度调整的基础。像素邻域的局部均值是平均灰度的测度，局部方差是对比度的测度。使用局部均值和方差可以开发出简单而强大的图像局部增强算法。

以下基于 Rafael C. Gonzalez “Digital Image Processing (4th.Ed.)” 中的方法和案例进行介绍。

增强后的图像 g(x,y) 与原始图像 f(x,y) 的修正公式为：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲g(x,y)&=\begin{…

如果待增强区域相对平均灰度更暗，可以选择 $k_0=0,k_1=0.1$；如果待增强区域的对比度很低，可以选择 $k_2=0,k_3=0.1$。

需要指出的是，这种方法只对某些特殊类型的图像有效，而且需要针对具体图像进行 ROI 设置和参数调节，才能取得较好的图像增强效果。

基本例程：1.61 直方图统计量图像增强

    # # 1.63 直方图统计量图像增强
    img = cv2.imread("../images/Fig0326a.tif", flags=0)  # flags=0 读取为灰度图像

    imgROI = img[12:120, 12:120]
    maxImg, maxROI = img.max(), imgROI.max()
    const = maxImg / maxROI
    imgHSE = enhanceHistStat(img, const)  # 子程序：直方图统计量增强 (自定义方法)

    plt.figure(figsize=(10, 6))
    plt.subplot(131), plt.title("Original image"), plt.axis('off')
    plt.imshow(img, cmap='gray', vmin=0, vmax=255)
    plt.subplot(132), plt.title("Global equalize histogram"), plt.axis('off')
    imgEqu = cv2.equalizeHist(img)  # 使用 cv2.qualizeHist 完成直方图均衡化变换
    plt.imshow(imgEqu, cmap='gray', vmin=0, vmax=255)
    plt.subplot(133), plt.title("Histogram statistic enhance"), plt.axis('off')
    plt.imshow(imgHSE, cmap='gray', vmin=0, vmax=255)
    plt.show()

4.6 直方图反向投影（反向追踪）

直方图反向投影是一种在输入图像中查找与特定模板图像匹配最佳的点或区域的方法，可以对特定颜色物体、特定灰度物体进行查找、跟踪，常用于图像查找、图像分割。

直方图反向投影处理的原理，是计算某一特征的直方图模型，再使用该模型去寻找图像中存在的特征。

直方图反向投影处理的过程，首先建立模板区域的直方图，再将直方图投影到输入图像，计算输入图像中每个像素点的像素值与直方图匹配概率，得到概率图像并以一定阈值进行二值化处理。

OpenCV 提供的函数 cv2.calcBackProject() 可以用来做直方图反向投影。

函数说明：

cv2.calcBackProject(images, channels, hist, ranges, scale[, dst]) → dst

参数说明：

• images：颜色对比度的阈值，可选项，默认值 8

• channels： 计算反向投影的图像通道

• hist： 查找模板区域的直方图

• ranges：每个维度中直方图单元边界的数组

• scale：反向投影输出的缩放比例

• 返回值 dst：返回反向投影的输出图像

基本例程：1.64 直方图反向投影追踪

    # 1.64 直方图反向投影
    roi = cv2.imread("../images/BallFrag.png", flags=1)  # 查找的图像区域
    target = cv2.imread("../images/imgBall.png", flags=1)  # 被查找的目标图像

    hsvRoi = cv2.cvtColor(roi, cv2.COLOR_BGR2HSV)
    hsvTar = cv2.cvtColor(target, cv2.COLOR_BGR2HSV)

    histRoi = cv2.calcHist([hsvRoi], [0, 1], None, [180, 256], [0, 180, 0, 256])  # 计算目标直方图
    cv2.normalize(histRoi, histRoi, 0, 255, cv2.NORM_MINMAX)  # 归一化 ->[0,255]

    dst = cv2.calcBackProject([hsvTar], [0, 1], histRoi, [0, 180, 0, 256], 1)  # 反向投影
    disc = cv2.getStructuringElement(cv2.MORPH_ELLIPSE, (5, 5))  # 定义椭圆结构形状
    imgConv = cv2.filter2D(dst, -1, disc)  # 图像卷积

    ret, thresh = cv2.threshold(imgConv, 100, 255, 0)  # 图像二值化处理，得到掩模模板
    imgTrack = cv2.bitwise_and(target, target, mask=thresh)  # 以 thresh 为掩模按位与，显示查找区域

    plt.figure(figsize=(10,6))
    plt.subplot(131), plt.imshow(cv2.cvtColor(target, cv2.COLOR_BGR2RGB)), plt.title("target image"), plt.axis('off')
    plt.subplot(132), plt.imshow(thresh, 'gray'), plt.title("tracking mask"), plt.axis('off')
    plt.subplot(133), plt.imshow(cv2.cvtColor(imgTrack, cv2.COLOR_BGR2RGB)), plt.title("tracking result"), plt.axis('off')
    plt.show()

---

版权声明：

注：本文中部分原始图片来自 Rafael C. Gonzalez “Digital Image Processing, 4th.Ed.” Fig3.10b，特此致谢。

欢迎关注『Python 小白从零开始 OpenCV 学习课 @ youcans』 原创作品

原创作品，转载必须标注原文链接：https://blog.csdn.net/youcans/article/details/121328057

Copyright 2021 youcans, XUPT

Crated：2021-11-18

欢迎关注 『Python小白从零开始 OpenCV 学习课』 系列，持续更新

Python 大白从零开始 OpenCV 学习课-1.安装与环境配置
Python 大白从零开始 OpenCV 学习课-2.图像读取与显示
Python 大白从零开始 OpenCV 学习课-3.图像的创建与修改
Python 大白从零开始 OpenCV 学习课-4.图像的叠加与混合
Python 大白从零开始 OpenCV 学习课-5.图像的几何变换
Python 大白从零开始 OpenCV 学习课-6. 灰度变换与直方图处理