【堆排序】-详细例子以及C++实现

详细记录一下自己理解的过程，方便后续查看，结合例子理解了整个过程，程序实现按照思路写就可以了。

这里的根节点从1开始编号！！

1. 堆

堆是一棵完全二叉树
大根堆： 任何一个父节点的值不小于其左右孩子结点的值，即：
$$key[i]\ge key[2i]\&\&key[i]\ge key[2i+1]$$
堆顶元素记录的是最大的关键字。

小根堆： 任何一个父节点的值不大于其左右孩子结点的值，即：
$$key[i]\le key[2i]\&\&key[i]\le key[2i+1]$$
堆顶元素记录的是最小的关键字。

2. 堆排序

2.1 步骤

升序用大根堆，降序就用小根堆
在升序排序中，我们会将堆反复调整为大根堆，这样在将堆顶元素与其子树结点交换的过程中，才能将最大的关键字（堆顶元素）调整到后面，从而得到一个有序序列。

堆排序主要有以下两个步骤：

• 建初堆：从$\lfloor n/2\rfloor$开始，依次将$\lfloor n/2\rfloor 、\lfloor n/2\rfloor -1\cdots ,1$作为根的子树都调整为堆
• 交换并调整，从$i=n$开始
  * 交换 $\mathrm{r}[1]$ 和 $\mathrm{r}[i]$, 则 $\mathrm{r}[i]$ 为关键字最大（$\mathrm{r}[1]\cdots \mathrm{r}[i]$最大）的记录，将 $\mathrm{r}[1]\cdots \mathrm{r}[i-1]$ 重新调整为堆,
  * $i=i-1$，循环 $n$ 次, 直到交换 $\mathrm{r}[1]$ 和 $\mathrm{r}[2]$ 为止，得到一个有序序列 $\mathrm{r}[1]\cdots \mathrm{r}[n]$ 。

【建初堆】
要将一个无序序列调整为堆，就必须将其所对应的完全二叉树中以每一结点为根的子树都调整为堆。只有一个结点的树必是堆，而在完全二叉树中，所有序号大于$\lfloor n/2\rfloor$ 的结点都是叶子结点，因此以这些结点为根的子树均已是堆。这样，只需利用筛选法，从最后一个分支结点$\lfloor n/2\rfloor$开始，依次将序号为$\lfloor n/2\rfloor 、\lfloor n/2\rfloor -1、\cdots 、1$的结点作为根的子树都调整为堆即可。

【筛选法调整堆】大根堆
设需要调整以$\mathrm{r}[j]$为根节点的子树
从 $\mathrm{r}[2j]$ 和 $\mathrm{r}[2j+1$ ]（左孩子结点和右孩子结点）中选出关键字较大者，假设 $\mathrm{r}[2j+1]$ 的关键字较大，比较 $\mathrm{r}[j]$ 和 $\mathrm{r}[2j+1]$ 的关键字。
(1) 若 $\mathrm{r}[j]$$>=\mathrm{r}[2j+1]$, 说明以 $\mathrm{r}[j]$ 为根的子树已经是大根堆，不必做任何调整。
(2) 若 $\mathrm{r}[j]$ $<\mathrm{r}[2j+1]$, 交换 $\mathrm{r}[j]$ 和 $\mathrm{r}[2j+1]$ 。交换后, 以 $\mathrm{r}[2j]$ 为根的子树仍是大根堆（没有对其进行操作）, 如果以 $\mathrm{r}[2j+1]$ 为根的子树不是堆, 则重复上述过程，将以 $\mathrm{r}[2j+1]$ 为根的子树调整为堆，直至进行到叶子结点为止。

2.2 举例

【举例】
对无序序列$\{49,38,65,97,76,13,27,\overline{49}\}$进行升序排序。
1) 建初堆
建立大根堆
下图是该无序序列组成的完全二叉树，长度$n=8$，叶子结点已经是堆，则我们从最后一个非叶子结点开始用筛选法调整为堆，即$j=\lfloor 8/2\rfloor =4$这个元素（97）开始。

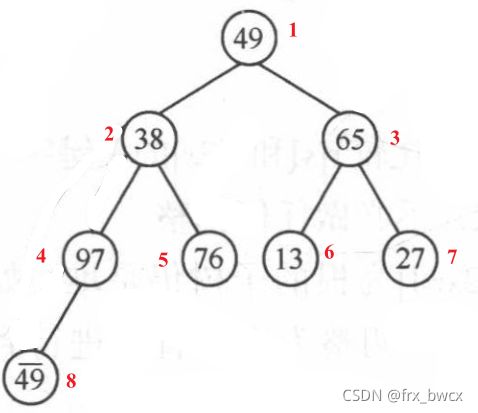
由于$97>\overline{49}$，则无需交换，同理，$65$也大于其左右孩子结点的值，无需交换。
接下来将以$38(j=2)$作为根结点的子树调整为大根堆：
孩子结点中较大值是$97(2j=4)$，且$97>38(r[2j]>r[j])$，则交换（因为我们要建立的是大根堆，所以父节点的值要大于其孩子结点）。

此时，以$76(2j+1=5)$为根结点的子树没有改变，仍然是大根堆。但是以$38(2j=4)]$为根结点的子树不是大根堆，应该继续调整，将其与孩子结点交换。

此时，以编号$j=2$为根节点的树已经是大根堆，筛选38结束。
接下来是调整以编号$j=1$为根节点的树，使其是大根堆，过程如下：

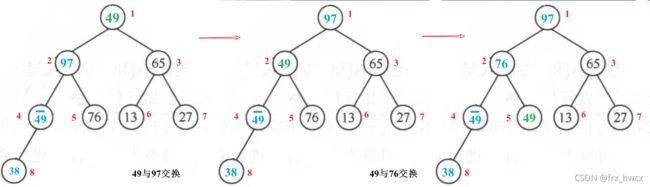
2) 交换并调整堆

注： 设我们当前需要将堆顶元素$r[1]$和$r[i]$进行交换，则交换后$r[i]\cdots r[n]$是有序的， $r[1]\cdots r[i-1]$是待排序序列，为了保证堆顶元素$r[1]$是待排序序列中的最大值，我们还需要将$r[1]\cdots r[i-1]$重新调整为大根堆，以便后续的交换。

利用上面已经建立好的大根堆，我们从$i=n$开始

• 交换$r[1]$和$r[n]$
  
  最大的关键字已经在其正确的位置，$r[i]\cdots r[n]$已经有序。
• 调整为堆
  接下来需要找到待排序序列$r[1]\cdots r[i-1]$中的最大值，且将其放在堆顶，所以我们将$r[1]\cdots r[i-1]$重新调整为堆，调整方法和建初堆时用到的调整方法一样。
  以当前序列为例，此时以$r[1]=38$为根结点到$r[7]=27$的子树明显不是大根堆，所以我们从根结点开始调整。

• $38>76$，交换，此时以$65$为根结点的子树是没有变的，还是大根堆，所以不用再判断它
• 交换后，以$38$为根结点，$49$和$\overline{49}$为左右孩子结点的子树仍然不是大根堆，继续交换，这里我们交换左孩子结点
• 因为$97$属于已排序序列，故不参与判断，调整结束

调整为堆的过程如图：

接下来，$i=i-1$，重复上述过程，交换然后调整，直到交换$r[1]$与$r[2]$。
当$i=n-1$时：

当$i=n-2,\cdots ,1$时（直接引用的书上的图片）：

3. 程序实现

堆排序（升序）

#include 
#include 
#include 

using namespace std;

void heapSort(vector<int> &nums);
void createHeap(vector<int> &nums, int n);
void heapAdjust(vector<int> &nums, int rootIdx, int m);

int main() {
     
    vector<int> nums = {
     0, 49, 38, 65, 97, 76, 13, 27, 49};
    heapSort(nums);
    for (int x : nums){
     
        cout << x << " ";
    } // 0 13 27 38 49 49 65 76 97 
}

void heapSort(vector<int> &nums){
     
    int n = nums.size() - 1;
    // 建初堆
    createHeap(nums, n);
    // 调整为堆
    for (int i = n; i >= 1; i--){
     
        // 交换堆顶元素和待排序序列的最后一个元素
        swap(nums[1], nums[i]); // 交换后 i, ... ,n 已排序
        // 将 1, ... ,i - 1 重新调整为大根堆
        heapAdjust(nums, 1, i - 1);
    }
}
void createHeap(vector<int> &nums, int n){
     
    // 建初堆
    // n / 2 + 1, ... , n 都是堆！！所以从 n / 2 开始调整，依次调整 以n / 2, n / 2 - 1, n / 2 - 2, ... , 1作为根结点的子树
    for (int i = n / 2; i >= 1; i--){
     
        // 将以 i 为根结点，编号一直到 n 的子树调整为堆
        heapAdjust(nums, i, n);
    }
}
void heapAdjust(vector<int> &nums, int rootIdx, int m){
     
    // 调整为堆：将以 rootIdx 为根结点，编号一直到 m 的子树调整为大根堆
    
    int pivot = nums[rootIdx]; // 以建初堆时的38这个结点为例，rootIdx = 2，pivot = 38，m = 8
    int j = 2 * rootIdx; // 先设置为左孩子结点的下标
    for (j; j <= m; j *= 2){
      // 连续判断，交换后可能出现子树不是大根堆的情况
        // 判断左右孩子结点谁更大
        if (j < m && nums[j] < nums[j + 1]){
     
            j++;
        }
        
        if (pivot > nums[j]){
     
            // 如果当前根结点大于较大的孩子结点，则其本身就是大根堆，不需要再调整
            break;
        }else {
     
            // 否则交换根结点与较大孩子结点，这里赋值即可，还要继续判断交换后的下一层子树是否是大根堆，故更新根结点的下标
            nums[rootIdx] = nums[j]; // 以建初堆时的38这个结点为例，j = 4, nums[2] = 97; j = 8, nums[4] = 49
            rootIdx = j; // 以建初堆时的38这个结点为例，j = 4, rootIdx = 4; j = 8, rootIdx = 8
        }
        // j = 8 --> j = 16 跳出循环
    }
    
    // 将根结点的值放到最终对应下标的位置
    nums[rootIdx] = pivot; // rootIdx = 8, pivot = 38
}

4. 参考资料

• 数据结构C语言版 第二版（严尉敏）