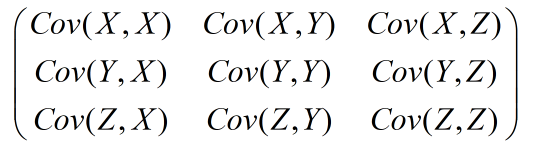协方差矩阵数学原理,numpy计算协方差矩阵(np.cov)函数详解与源码剖析
协方差矩阵详解以及numpy计算协方差矩阵(np.cov)
协方差矩阵详解
均值,标准差与方差
由简单的统计学基础知识,我们有如下公式:
X ˉ = ∑ i = 1 n X i n \bar X{\rm{ = }}\frac{ {\sum\limits_{i = 1}^n { {X_i}} }}{ {\rm{n}}} Xˉ=ni=1∑nXi
S = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 S = \sqrt {\frac{ {\sum\limits_{i = 1}^n { { {({X_i} - \bar X)}^2}} }}{ {n - 1}}} S=n−1i=1∑n(Xi−Xˉ)2
S 2 = ∑ i = 1 n ( X i − X ˉ ) 2 n − 1 {S^2} = \frac{ {\sum\limits_{i = 1}^n { { {({X_i} - \bar X)}^2}} }}{ {n - 1}} S2=n−1i=1∑n(Xi−Xˉ)2
其中 X ˉ \bar X Xˉ是样本均值,反映了n个样本观测值的整体大小情况。
S S S是样本标准差,反应的是样本的离散程度。标准差越大,数据越分散。
S 2 S^2 S2是样本方差,是 S S S的平方。
均值虽然可以在一定程度上反应数据的整体大小,但是仍然不能反应数据的内部离散程度。而标准差和方差弥补了这一点。
但是标准差和方差都是针对一维数组的,即1 x d数组。该数组的行代表的是一个随机变量(可理解为属性),如工资等。每一列代表一个观测值。如果一个事物具有多种属性,即有多个随机变量,那么我们会得到一个var_num x d数组。该数组的每一行都是一个随机变量(属性),每一列代表着一个在这些属性维度上的观测值样本。如果我们想要分析该事物,那么仅仅将其剥离为单独的1 x d去求其标准差是不够的,我们还需要关注这些随机变量(属性)variable内部之间的联系。如工资和年龄的联系,工资和技术水平的联系等。
所以便自然而然的引入了协方差。
协方差
两个随机变量的协方差反映了这两个随机变量一致的分散程度有多大。
通俗的讲,协方差反映了两个随机变量的正负相关关系。
由方差的公式,我们可以类比得出协方差的公式:
v a r ( X ) = S 2 = ∑ i = 1 n ( X i − X ˉ ) ( X i − X ˉ ) n − 1 {\mathop{\rm var}} (X) = {S^2} = \frac{ {\sum\limits_{i = 1}^n {({X_i} - \bar X)({X_i} - \bar X)} }}{ {n - 1}} var(X)=S2=n−1i=1∑n(Xi−Xˉ)(Xi−Xˉ)
c o v ( X , Y ) = ∑ i = 1 n ( X i − X ˉ ) ( Y i − Y ˉ ) n − 1 = E ( ( X − E ( X ) ) ( Y − E ( Y ) ) ) {\mathop{\rm cov}} (X,Y) = \frac{ {\sum\limits_{i = 1}^n {({X_i} - \bar X)({Y_i} - \bar Y)} }}{ {n - 1}} = E((X - E(X))(Y - E(Y))) cov(X,Y)=n−1i=1∑n(Xi−Xˉ)(Yi−Yˉ)=E((X−E(X))(Y−E(Y)))
相关系数 ρ \rho ρ与协方差直接有如下关系:
ρ = C o v ( X , Y ) σ X σ Y = E ( ( X − E ( X ) ) ( Y − E ( Y ) ) ) σ X σ Y = E ( ( X − E ( X ) σ X ) ( Y − E ( Y ) σ Y ) \rho = \frac{ {Cov(X,Y)}}{ { {\sigma _X}{\sigma _Y}}} = \frac{ {E((X - E(X))(Y - E(Y)))}}{ { {\sigma _X}{\sigma _Y}}} = E((\frac{ {X - E(X)}}{ { {\sigma _X}}})(\frac{ {Y - E(Y)}}{ { {\sigma _Y}}}) ρ=σXσYCov(X,Y)=σXσYE((X−E(X))(Y−E(Y)))=E((σXX−E(X))(σYY−E(Y))
从上述公式可见,相关系数 ρ \rho ρ实际上也是一种特殊的协方差。相关系数是数据X和Y做了归一化 x = ( X − X ˉ ) σ X x = \frac{ {(X - \bar X)}}{ { {\sigma _X}}} x=σX(X−Xˉ), y = ( Y − Y ˉ ) σ Y y = \frac{ {(Y - \bar Y)}}{ { {\sigma _Y}}} y=σY(Y−Yˉ)之后的协方差。 x , y x,y x,y的方差为1,期望为0。有:
ρ ( X , Y ) = c o v ( x , y ) \rho(X,Y) = cov(x,y) ρ(X,Y)=cov(x,y)
协方差的意义此时应该很清晰了。
协方差矩阵
对于具有很多个随机变量的数据,随机变量之间两两都具有一个协方差,这样便形成了一个协方差矩阵。
假设我们有一组数据,其具有三个随机变量,n个观测值:
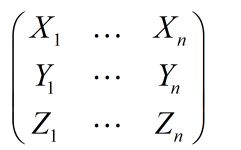
我们可以使用一种便捷的矩阵乘法来计算协方差矩阵。设原数据数组为 X X X。先对X进行处理,求X每一个随机变量的均值。然后对于每一行,减去该行随机变量的均值,得到 X ′ X^{'} X′,记协方差矩阵为 M M M,那么就有:
M = X ′ X ′ T n − 1 M = \frac{ {X^{'}{X^{'}}^{T}}}{ {n-1}} M=n−1X′X′T
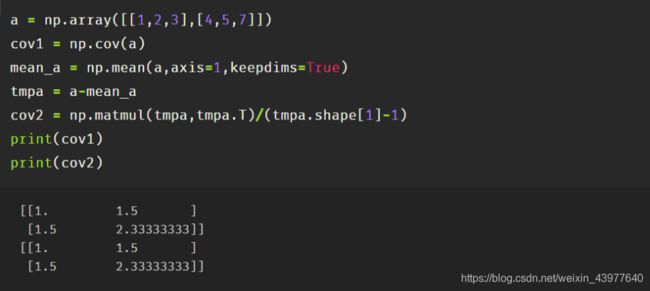
用代码描述可能更加清晰:
a = np.array([[1,2,3],[4,5,7]])
cov1 = np.cov(a)
mean_a = np.mean(a,axis=1,keepdims=True)
tmpa = a-mean_a
cov2 = np.matmul(tmpa,tmpa.T)/(tmpa.shape[1]-1)
print(cov1)
print(cov2)
numpy计算协方差矩阵np.cov()
语法
numpy.cov(m,y=None,rowvar=True,bias=False,ddof=None,fweights=None,aweights=None,dtype)
用于计算给定矩阵和权值的协方差矩阵。
Parameters
- m:array_like
A 1-D or 2-D array containing multiple variables and observations. Each row of m represents a variable, and each column a single observation of all those variables. Also see rowvar below.
一维或者二维数组,包含有多个随机变量和观测值。m的每一行代表一个随机变量,每一列代表包含所有随机变量的一个观测值。当给一维数组时,相当于计算的就是方差。
- y:array_like,optional
An additional set of variables and observations. y has the same form as that of m.
额外的一组数据,y必须在在数据形式上与m一致。
如果m.shape = (var_num, obs_num),那么y.shape必须在第二维观测值个数上,即shape[1]与m保持一致,即y也得有obs_num个观测值。实际执行时,会先将这两组数据concatenate,然后再求解。
Example
a = np.array([[1,2,3],[4,5,7]])
b = np.array([[1,2,3,4],[4,5,6,7]])
cov = np.cov(a,b)
从执行结果上可见,报错。报错的具体描述便是,两组数据在dimension1不一致。
我们也可以从numpy.cov()源码中看到:
if y is not None:
y = array(y, copy=False, ndmin=2, dtype=dtype)
if not rowvar and y.shape[0] != 1:
y = y.T
X = np.concatenate((X, y), axis=0)
可见是对其进行了concatenate.
- bias: bool, optional
Default normalization (False) is by (N - 1), where N is the number of observations given (unbiased estimate). If bias is True, then normalization is by N. These values can be overridden by using the keyword ddof in numpy versions >= 1.5
默认的采用无偏估计,即除以(N-1),N是样本个数。可以被ddof所覆盖。
- rowvar : bool, optional
If
rowvaris True (default), then each row represents a
variable, with observations in the columns. Otherwise, the relationship
is transposed: each column represents a variable, while the rows
contain observations.
rowvar指定了行列谁为随机变量的问题。默认为True,即行代表一个随机变量。而列代表观测值。如果为False,那么列代表随机变量,而行代表观测值。
- ddof : int, optional
If not
Nonethe default value implied bybiasis overridden.
Note thatddof=1will return the unbiased estimate, even if both
fweightsandaweightsare specified, andddof=0will return
the simple average. See the notes for the details. The default value
isNone.
.. versionadded:: 1.5
ddof,duplicated degrees of freedom,即重复无效的自由度。参见源码详解。
- fweights : array_like, int, optional
1-D array of integer frequency weights; the number of times each
observation vector should be repeated.
.. versionadded:: 1.10
一维int数组,shape[0]应当与数据的观测值个数一致(即当rowvar=True时候的shape[1])。指定每个观测值的频率权重,即这个观测值向量(column)应该被重复计算几次。
- aweights : array_like, optional
1-D array of observation vector weights. These relative weights are
typically large for observations considered “important” and smaller for
observations considered less “important”. Ifddof=0the array of
weights can be used to assign probabilities to observation vectors.
.. versionadded:: 1.10
一维数组,其shape[0]同样的,应该与观测值个数一致。指定的是每个计算权重,即较重要的观测值其aweight大一些,不那么重要的可以小一些。当ddof为0的时候,相当于观测值的概率。
- Return:
- out: ndarray: The covariance matrix of the variables.
Example
由于不太直观,所以不举例。分析一下源码。
源码
if ddof is not None and ddof != int(ddof): # 这里说明ddof必须是int类型
raise ValueError(
"ddof must be integer")
# Handles complex arrays too
m = np.asarray(m) # 所以m的输入类型可以是lists, lists of tuples
#tuples, tuples of tuples, tuples of lists and ndarrays.
if m.ndim > 2: # 不能超过两维
raise ValueError("m has more than 2 dimensions")
if y is None: # 如果y是None,返回数组类型取原数组类型
# 与np.float64精度高的那一个。
dtype = np.result_type(m, np.float64)
else: # 有y输入则先处理y,判断y的维度,再判断数据类型
y = np.asarray(y)
if y.ndim > 2:
raise ValueError("y has more than 2 dimensions")
dtype = np.result_type(m, y, np.float64)
X = array(m, ndmin=2, dtype=dtype)
if not rowvar and X.shape[0] != 1: # 如果rowvar为False就转置
X = X.T
if X.shape[0] == 0:
return np.array([]).reshape(0, 0)
if y is not None: # 对y进行处理
y = array(y, copy=False, ndmin=2, dtype=dtype)
if not rowvar and y.shape[0] != 1: # 判断rowvar是否转置
y = y.T
X = np.concatenate((X, y), axis=0) # concatenate
if ddof is None: # 如果未指定ddof
if bias == 0: # 如果指定了bias=0,ddof=1,无偏
ddof = 1
else: # 否则ddof=0
ddof = 0
# Get the product of frequencies and weights
w = None
if fweights is not None:
fweights = np.asarray(fweights, dtype=float)
if not np.all(fweights == np.around(fweights)): # round进行取整
# 取整后判断是否全部相等,来判断全都是整数,必须全是整数,否则报错
raise TypeError(
"fweights must be integer")
if fweights.ndim > 1: # 必须一维
raise RuntimeError(
"cannot handle multidimensional fweights")
if fweights.shape[0] != X.shape[1]: # 必须与观测数一致
raise RuntimeError(
"incompatible numbers of samples and fweights")
if any(fweights < 0): #必须全部为正值
raise ValueError(
"fweights cannot be negative")
w = fweights # 将fweight赋给w
if aweights is not None:
aweights = np.asarray(aweights, dtype=float)
if aweights.ndim > 1:
raise RuntimeError(
"cannot handle multidimensional aweights")
if aweights.shape[0] != X.shape[1]:
raise RuntimeError(
"incompatible numbers of samples and aweights")
if any(aweights < 0):
raise ValueError(
"aweights cannot be negative")
if w is None:
w = aweights # 如果fweight为空,就直接把aweight赋给w
else:
w *= aweights # 否则w = fweight * aweight
avg, w_sum = average(X, axis=1, weights=w, returned=True)
# 以列为操作单元,求每一个随便变量的所有观测值在权重w下的均值。
# w_sum为w的所有元素的和(权重和)。
w_sum = w_sum[0]
# Determine the normalization
if w is None: # 如果w为None,那么直接用X的观测值个数(列数)减ddof
fact = X.shape[1] - ddof
elif ddof == 0: # w不为空,ddof等于0,需要除以的分母就是 w_sum
fact = w_sum
elif aweights is None: # w不为空,aweight为空,ddof不为0
# 直接用 w_sum-ddof(因为此时的w_sum就相当于重复后的观测值个数)
fact = w_sum - ddof
else: # w不为空,aweight也不为空, fweight也不为空,ddof != 0
# fact就相当于w_sum减去以w为权重的aweight的平均值乘以ddof
# 当aweigth=None的时候,是这个公式的一个特殊情况
# 在这里猜测:ddof: duplicated degreeds of freedom
# 即重复无效的自由度
fact = w_sum - ddof*sum(w*aweights)/w_sum
if fact <= 0:
warnings.warn("Degrees of freedom <= 0 for slice",
RuntimeWarning, stacklevel=3)
fact = 0.0
X -= avg[:, None] # X减去均值
if w is None:
X_T = X.T
else:
X_T = (X*w).T # 乘以权重
c = dot(X, X_T.conj()) # X 乘以 X的转置的复共轭矩阵(对标量而言就是转置)
c *= np.true_divide(1, fact) # 再除以fact
return c.squeeze() # 删去c中dim为1的维度,输出。
以上就是我对np.cov()的全部解读。
如果觉得文章对您有帮助,可以点个赞,是对作者最大的鼓励。