数学建模智能优化算法之免疫算法(IA)案例附Matlab代码
读书使人充实,讨论使人机智,笔记使人准确…。凡有所学,皆成性格。
———— (英国)培根
文章目录
免疫算法与生物免疫系统概念的对应关系
| 生物免疫系统 | 免疫算法 |
|---|---|
| 抗原 | 优化问题 |
| 抗体(B细胞) | 优化问题的可行解 |
| 亲和度 | 可行解的质量 |
| 细胞活化 | 免疫选择 |
| 细胞分化 | 个体克隆 |
| 亲和度成熟 | 变异 |
| 克隆抑制 | 克隆抑制 |
| 动态维持平衡 | 种群刷新 |
关键参数说明
| 参数 | 取值 |
|---|---|
| 抗体种群大小 N p N_{p} Np | N p N_{p} Np取10~100较为合适,一般不超过200 |
| 免疫选择比例 | 一般可以取抗体种群大小 N p N_{p} Np的10%~50% |
| 抗体克隆扩增的倍数 | 一般取5~10倍 |
| 种群刷新比例 | 一般不超过抗体种群的50% |
| 最大进化代数G | 一般G取100~500 |
[求最小值]计算函数 f ( x ) = ∑ i = 1 n x i 2 ( − 20 ≤ x i ≤ 20 ) f(x)=\sum_{i=1}^nx_{i}^2\quad(-20 \leq x_{i} \leq 20) f(x)=∑i=1nxi2(−20≤xi≤20) 的最小值,其中个体x的维数n=10。这是一个简单的平方和函数,只有一个极小点x=(0,0,…,0),理论最小值f(0,0,…,0)=0
解:仿真过程如下:
(1)初始化免疫个体维数为D=10,免疫种群个体数为 N p N_{p} Np=100,最大免疫代数为G=500,变异概率为 P m P_{m} Pm=0.7,激励度系数为alfa=1,belta=1,相似度阈值为detas=0.2,克隆个数为 N c l N_{cl} Ncl=10。
(2)随机产生初始种群,计算个体亲和度、抗体浓度和激励度,并按激励度排序。
(3)取激励度前 N p / 2 N_{p}/2 Np/2个个体进行克隆、变异、克隆抑制的免疫操作,免疫后的种群进行激励度计算。
(4)随机生成 N p N_{p} Np/2$个个体的新种群,并计算个体亲和度、抗体浓度和激励度;免疫种群和随机种群合并,按激励度排序,进行免疫迭代。
(5)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
优化结束后,其亲和度进化曲线如图所示,优化后的结果为x=[0.0002 -0.0035 -0.0036 0.0007 0.0000 -0.0009 -0.0004 -0.0005 -0.0010 0.0070],函数 f ( x ) f(x) f(x)的最小值为7.626×10-5
MATLAB源程序如下:
%%%%%%%%%%%%%%%%%免疫算法求函数极值%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
D=10; %免疫个体维数
NP=100; %免疫个体数目
Xs=20; %取值上限
Xx=-20; %取值下限
G=500; %最大免疫代数
pm=0.7; %变异概率
alfa=1; %激励度系数
belta=1; %激励度系数
detas=0.2; %相似度阈值
gen=0; %免疫代数
Ncl=10; %克隆个数
deta0=1*Xs; %邻域范围初值
%%%%%%%%%%%%%%%%%%%%%%%初始种群%%%%%%%%%%%%%%%%%%%%%%%%
f=rand(D,NP)*(Xs-Xx)+Xx;
for np=1:NP
FIT(np)=func1(f(:,np));
end
%%%%%%%%%%%%%%%%%计算个体浓度和激励度%%%%%%%%%%%%%%%%%%%
for np=1:NP
for j=1:NP
nd(j)=sum(sqrt((f(:,np)-f(:,j)).^2));
if nd(j)<detas
nd(j)=1;
else
nd(j)=0;
end
end
ND(np)=sum(nd)/NP;
end
FIT = alfa*FIT- belta*ND;
%%%%%%%%%%%%%%%%%%%激励度按升序排列%%%%%%%%%%%%%%%%%%%%%%
[SortFIT,Index]=sort(FIT);
Sortf=f(:,Index);
%%%%%%%%%%%%%%%%%%%%%%%%免疫循环%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
for i=1:NP/2
%%%%%%%%选激励度前NP/2个体进行免疫操作%%%%%%%%%%%
a=Sortf(:,i);
Na=repmat(a,1,Ncl);
deta=deta0/gen;
for j=1:Ncl
for ii=1:D
%%%%%%%%%%%%%%%%%变异%%%%%%%%%%%%%%%%%%%
if rand<pm
Na(ii,j)=Na(ii,j)+(rand-0.5)*deta;
end
%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%
if (Na(ii,j)>Xs) | (Na(ii,j)<Xx)
Na(ii,j)=rand * (Xs-Xx)+Xx;
end
end
end
Na(:,1)=Sortf(:,i); %保留克隆源个体
%%%%%%%%%%克隆抑制,保留亲和度最高的个体%%%%%%%%%%
for j=1:Ncl
NaFIT(j)=func1(Na(:,j));
end
[NaSortFIT,Index]=sort(NaFIT);
aFIT(i)=NaSortFIT(1);
NaSortf=Na(:,Index);
af(:,i)=NaSortf(:,1);
end
%%%%%%%%%%%%%%%%%%%%免疫种群激励度%%%%%%%%%%%%%%%%%%%
for np=1:NP/2
for j=1:NP/2
nda(j)=sum(sqrt((af(:,np)-af(:,j)).^2));
if nda(j)<detas
nda(j)=1;
else
nda(j)=0;
end
end
aND(np)=sum(nda)/NP/2;
end
aFIT = alfa*aFIT- belta*aND;
%%%%%%%%%%%%%%%%%%%%%%%种群刷新%%%%%%%%%%%%%%%%%%%%%%%
bf=rand(D,NP/2)*(Xs-Xx)+Xx;
for np=1:NP/2
bFIT(np)=func1(bf(:,np));
end
%%%%%%%%%%%%%%%%%%%新生成种群激励度%%%%%%%%%%%%%%%%%%%%
for np=1:NP/2
for j=1:NP/2
ndc(j)=sum(sqrt((bf(:,np)-bf(:,j)).^2));
if ndc(j)<detas
ndc(j)=1;
else
ndc(j)=0;
end
end
bND(np)=sum(ndc)/NP/2;
end
bFIT = alfa*bFIT- belta*bND;
%%%%%%%%%%%%%%免疫种群与新生种群合并%%%%%%%%%%%%%%%%%%%
f1=[af,bf];
FIT1=[aFIT,bFIT];
[SortFIT,Index]=sort(FIT1);
Sortf=f1(:,Index);
gen=gen+1;
trace(gen)=func1(Sortf(:,1));
end
%%%%%%%%%%%%%%%%%%%%%%%输出优化结果%%%%%%%%%%%%%%%%%%%%%%%%
Bestf=Sortf(:,1); %最优变量
trace(end); %最优值
figure,plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('亲和度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%亲和度函数%%%%%%%%%%%%%%%%%%%%%%
function result=func1(x)
summ=sum(x.^2);
result=summ;
end
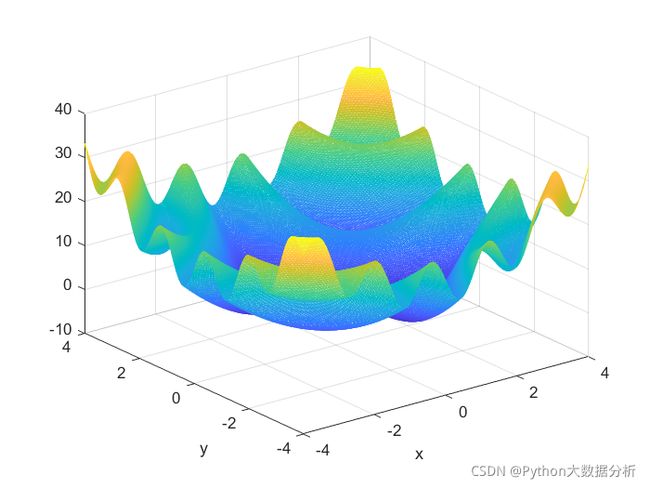
[求最小值]函数 f ( x , y ) = 5 s i n ( x y ) + x 2 + y 2 f(x,y)=5sin(xy)+x^2+y^2 f(x,y)=5sin(xy)+x2+y2的最小值,其中x的取值范围为[-4,4],y的取值范围为[-4,4]。这是一个有多个局部极值的函数,其函数值图形如图所示,其MATLAB实现程序如下
%%%%%%%%%f(x,y)=5*sin(x*y)+x*x+y*y%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
x=-4:0.02:4;
y=-4:0.02:4;
N=size(x,2);
for i=1:N
for j=1:N
z(i,j)=5*sin(x(i)*y(j))+x(i)*x(i)+y(j)*y(j);
end
end
mesh(x,y,z)
xlabel('x')
ylabel('y')
解:仿真过程如下:
(1)初始化免疫个体维数为D=2,免疫种群个体数为 N p N_{p} Np=50,最大免疫代数为G=200,变异概率为 P m P_{m} Pm=0.7,激励度系数为alfa=2,belta=1,相似度阈值为detas=0.2,克隆个数为 N c l N_{cl} Ncl=5;(2)随机产生初始种群,计算个体亲和度、抗体浓度和激励度,并按激励度排序。
(3)取激励度前 N p / 2 N_{p}/2 Np/2个个体进行克隆、变异、克隆抑制的免疫操作;免疫后的种群进行激励度计算。
(4)随机生成 N p / 2 N_{p}/2 Np/2个个体的新种群,并计算个体亲和度、抗体浓度和激励度;免疫种群和随机种群合并,按激励度排序,进行免疫迭代。
(5)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
优化结束后,其亲和度进化曲线如图4.4所示,优化后的结果为:x=1.0767,y=-1.0767,函数 f ( x , y ) f(x,y) f(x,y)的最小值为-2.264
MATLAB源程序如下:
%%%%%%%%%%%%%%%%%免疫算法求函数极值%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
D=2; %免疫个体维数
NP=50; %免疫个体数目
Xs=4; %取值上限
Xx=-4; %取值下限
G=200; %最大免疫代数
pm=0.7; %变异概率
alfa=2; %激励度系数
belta=1; %激励度系数
detas=0.2; %相似度阈值
gen=0; %免疫代数
Ncl=5; %克隆个数
deta0=0.5*Xs; %邻域范围初值
%%%%%%%%%%%%%%%%%%%%%%%初始种群%%%%%%%%%%%%%%%%%%%%%%%%
f=rand(D,NP)*(Xs-Xx)+Xx;
for np=1:NP
FIT(np)=func2(f(:,np));
end
%%%%%%%%%%%%%%%%%计算个体浓度和激励度%%%%%%%%%%%%%%%%%%%
for np=1:NP
for j=1:NP
nd(j)=sum(sqrt((f(:,np)-f(:,j)).^2));
if nd(j)<detas
nd(j)=1;
else
nd(j)=0;
end
end
ND(np)=sum(nd)/NP;
end
FIT = alfa*FIT- belta*ND;
%%%%%%%%%%%%%%%%%%%激励度按升序排列%%%%%%%%%%%%%%%%%%%%%%
[SortFIT,Index]=sort(FIT);
Sortf=f(:,Index);
%%%%%%%%%%%%%%%%%%%%%%%%免疫循环%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
for i=1:NP/2
%%%%%%%%选激励度前NP/2个体进行免疫操作%%%%%%%%%%%
a=Sortf(:,i);
Na=repmat(a,1,Ncl);
deta=deta0/gen;
for j=1:Ncl
for ii=1:D
%%%%%%%%%%%%%%%%%变异%%%%%%%%%%%%%%%%%%%
if rand<pm
Na(ii,j)=Na(ii,j)+(rand-0.5)*deta;
end
%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%
if (Na(ii,j)>Xs) | (Na(ii,j)<Xx)
Na(ii,j)=rand * (Xs-Xx)+Xx;
end
end
end
Na(:,1)=Sortf(:,i); %保留克隆源个体
%%%%%%%%%%克隆抑制,保留亲和度最高的个体%%%%%%%%%%
for j=1:Ncl
NaFIT(j)=func2(Na(:,j));
end
[NaSortFIT,Index]=sort(NaFIT);
aFIT(i)=NaSortFIT(1);
NaSortf=Na(:,Index);
af(:,i)=NaSortf(:,1);
end
%%%%%%%%%%%%%%%%%%%%免疫种群激励度%%%%%%%%%%%%%%%%%%%
for np=1:NP/2
for j=1:NP/2
nda(j)=sum(sqrt((af(:,np)-af(:,j)).^2));
if nda(j)<detas
nda(j)=1;
else
nda(j)=0;
end
end
aND(np)=sum(nda)/NP/2;
end
aFIT = alfa*aFIT- belta*aND;
%%%%%%%%%%%%%%%%%%%%%%%种群刷新%%%%%%%%%%%%%%%%%%%%%%%
bf=rand(D,NP/2)*(Xs-Xx)+Xx;
for np=1:NP/2
bFIT(np)=func2(bf(:,np));
end
%%%%%%%%%%%%%%%%%%%新生成种群激励度%%%%%%%%%%%%%%%%%%%%
for np=1:NP/2
for j=1:NP/2
ndc(j)=sum(sqrt((bf(:,np)-bf(:,j)).^2));
if ndc(j)<detas
ndc(j)=1;
else
ndc(j)=0;
end
end
bND(np)=sum(ndc)/NP/2;
end
bFIT = alfa*bFIT- belta*bND;
%%%%%%%%%%%%%%免疫种群与新生种群合并%%%%%%%%%%%%%%%%%%%
f1=[af,bf];
FIT1=[aFIT,bFIT];
[SortFIT,Index]=sort(FIT1);
Sortf=f1(:,Index);
gen=gen+1;
trace(gen)=func2(Sortf(:,1));
end
%%%%%%%%%%%%%%%%%%%%%%%输出优化结果%%%%%%%%%%%%%%%%%%%%%%%%
Bestf=Sortf(:,1); %最优变量
trace(end); %最优值
figure,plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('亲和度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%亲和度函数%%%%%%%%%%%%%%%%%%%%%%
function value=func2(x)
value=5*sin(x(1)*x(2))+x(1)*x(1)+x(2)*x(2);
end
[旅行商问题](TSP)。假设有一个旅行商人要拜访全国31个省会城市,他需要选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。对路径选择的要求是:所选路径的路程为所有路径之中的最小值。全国31个省会城市的坐标为[1304 2312;3639 1315;4177 2244;37121399;3488 1535;3326 1556;3238 1229;4196 1004;4312 790;4386 570;3007 1970;2562 1756;2788 1491;2381 1676;1332695;3715 1678;3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2367;3394 2643;34393201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975]。
解:仿真过程如下:
(1)初始化免疫个体维数为城市个数N=31,免疫种群个体数为 N p N_{p} Np=200,最大免疫代数为G=1000,克隆个数为 N c l N_{cl} Ncl=10,计算任意两个城市间的距离矩阵D;
(2)随机产生初始种群,计算个体亲和度、并按激励度排序。
(3)在取亲和度前对 N p / 2 N_{p}/2 Np/2个个体进行克隆操作,并对每个源个体产生的克隆个体进行任意交换两个城市坐标的变异操作;然后计算其亲和度,进行克隆抑制操作,只保留亲和度最高的个体,从而产生新的免疫种群。
(4)随机生成 N p / 2 N_{p}/2 Np/2个个体的新种群,并计算个体亲和度、抗体浓度和激励度;免疫种群和随机种群合并,按激励度排序,进行免疫迭代。
(5)判断是否满足终止条件:若满足,则结束搜索过程,输出优化值;若不满足,则继续进行迭代优化。
优化后的路径如图所示,
亲和度进化曲线如图所示
MATLAB源程序如下:
%%%%%%%%%%%%%%%%%%%%%%%免疫算法求解决TSP问题%%%%%%%%%%%%%%%%%%%%%%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%初始化%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clear all; %清除所有变量
close all; %清图
clc; %清屏
C=[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;...
3238 1229;4196 1044;4312 790;4386 570;3007 1970;2562 1756;...
2788 1491;2381 1676;1332 695;3715 1678;3918 2179;4061 2370;...
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;...
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;...
2370 2975]; %31个省会城市坐标
N=size(C,1); %TSP问题的规模,即城市数目
D=zeros(N); %任意两个城市距离间隔矩阵
%%%%%%%%%%%%%%%%%%%%%求任意两个城市距离间隔矩阵%%%%%%%%%%%%%%%%%%%%%
for i=1:N
for j=1:N
D(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;
end
end
NP=200; %免疫个体数目
G=1000; %最大免疫代数
f=zeros(N,NP); %用于存储种群
for i=1:NP
f(:,i)=randperm(N); %随机生成初始种群
end
len=zeros(NP,1); %存储路径长度
for i=1:NP
len(i)=func3(D,f(:,i),N); %计算路径长度
end
[Sortlen,Index]=sort(len);
Sortf=f(:,Index); %种群个体排序
gen=0; %免疫代数
Ncl=10; %克隆个数
%%%%%%%%%%%%%%%%%%%%%%%%%%%免疫循环%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
while gen<G
for i=1:NP/2
%%%%%%%%%%%%选激励度前NP/2个体进行免疫操作%%%%%%%%%%%%%%%
a=Sortf(:,i);
Ca=repmat(a,1,Ncl);
for j=1:Ncl
p1=floor(1+N*rand());
p2=floor(1+N*rand());
while p1==p2
p1=floor(1+N*rand());
p2=floor(1+N*rand());
end
tmp=Ca(p1,j);
Ca(p1,j)=Ca(p2,j);
Ca(p2,j)=tmp;
end
Ca(:,1)=Sortf(:,i); %保留克隆源个体
%%%%%%%%%%%%克隆抑制,保留亲和度最高的个体%%%%%%%%%%%%%%
for j=1:Ncl
Calen(j)=func3(D,Ca(:,j),N);
end
[SortCalen,Index]=sort(Calen);
SortCa=Ca(:,Index);
af(:,i)=SortCa(:,1);
alen(i)=SortCalen(1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%种群刷新%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:NP/2
bf(:,i)=randperm(N); %随机生成初始种群
blen(i)=func3(D,bf(:,i),N); %计算路径长度
end
%%%%%%%%%%%%%%%%%%%%免疫种群与新种群合并%%%%%%%%%%%%%%%%%%%%%
f=[af,bf];
len=[alen,blen];
[Sortlen,Index]=sort(len);
Sortf=f(:,Index);
gen=gen+1;
trace(gen)=Sortlen(1);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%输出优化结果%%%%%%%%%%%%%%%%%%%%%%%%%%%
Bestf=Sortf(:,1); %最优变量
Bestlen=trace(end); %最优值
figure
for i=1:N-1
plot([C(Bestf(i),1),C(Bestf(i+1),1)],...
[C(Bestf(i),2),C(Bestf(i+1),2)],'bo-');
hold on;
end
plot([C(Bestf(N),1),C(Bestf(1),1)],...
[C(Bestf(N),2),C(Bestf(1),2)],'ro-');
title(['优化最短距离:',num2str(trace(end))]);
figure,plot(trace)
xlabel('迭代次数')
ylabel('目标函数值')
title('亲和度进化曲线')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%计算路线总长度%%%%%%%%%%%%%%%%%%%%%%%%
function len=func3(D,f,N)
len=D(f(N),f(1));
for i=1:(N-1)
len=len+D(f(i),f(i+1));
end
end
[1]包子阳 余继周 杨彬.智能优化算法及其MATLAB实例[M]电子工业出版社,2021