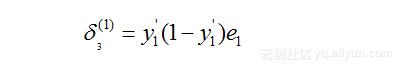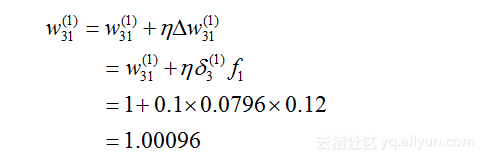BP算法双向传,链式求导最缠绵(深度学习入门系列之八)
摘要: 说到BP(Back Propagation)算法,人们通常强调的是反向传播,其实它是一个双向算法:正向传播输入信号,反向传播误差信息。接下来,你将看到的,可能是史上最为通俗易懂的BP图文讲解,不信?来瞅瞅并吐吐槽呗!
更多深度文章,请关注:https://yq.aliyun.com/cloud
系列文章:
一入侯门“深”似海,深度学习深几许(深度学习入门系列之一)
人工“碳”索意犹尽,智能“硅”来未可知(深度学习入门系列之二)
神经网络不胜语,M-P模型似可寻(深度学习入门系列之三)
“机器学习”三重门,“中庸之道”趋若人(深度学习入门系列之四)
Hello World感知机,懂你我心才安息 (深度学习入门系列之五)
损失函数减肥用,神经网络调权重(深度学习入门系列之六)
山重水复疑无路,最快下降问梯度(深度学习入门系列之七)
8.1 BP神经网络极简史
在神经网络(甚至深度学习)参数训练中,BP(Back Propagation)算法非常重要,它都占据举足轻重的地位。在提及BP算法时,我们常将它与杰弗里•辛顿(Geoffrey Hinton)的名字联系在一起。但实际上,辛顿还真不是第一个提出BP算法的人,就像爱迪生不是第一个发明电灯的人一样。但人们记住的,永远都是那个让电灯“飞入平常百姓家”的功勋人物爱迪生,而不是它的第一发明人美国人亨利·戈培尔(Henry Goebel)。
如果说辛顿就是BP算法的“爱迪生”,那谁是BP算法的“戈培尔”呢?他就是保罗·沃伯斯(Paul Werbos)。1974年,沃伯斯在哈佛大学博士毕业。在他的博士论文里,首次提出了通过误差的反向传播来训练人工神经网络[1]。事实上,这位沃伯斯不光是BP算法的开创者,他还是循环神经网络(Recurrent Neural Network,RNN)的早期开拓者之一。在后期的系列入门文章中,我们还会详细介绍RNN,这里暂且不表。
说到BP算法,我们通常强调的是反向传播,但其实呢,它是一个典型的双向算法。更确切来说,它的工作流程是分两大步走:(1)正向传播输入信号,输出分类信息(对于有监督学习而言,基本上都可归属于分类算法);(2)反向传播误差信息,调整全网权值(通过微调网络参数,让下一轮的输出更加准确)。
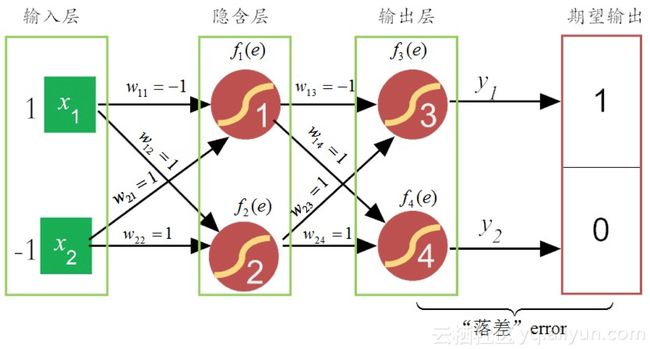
下面我们分别举例,说明这两个流程。为了简化问题描述,我们使用如图8-1所示的最朴素三层神经网络。在这个网络中,假设输入层的信号向量是[1, -1],输出层的目标向量为[1, 0],“学习率”η为0.1,权值是随机给的,这里为了演示方便,分别给予或“1”或“-1”的值。下面我们就详细看看BP算法是如何运作的?
图8-1 简易的三层神经网络
8.2.1正向传播信息
正向传播信息,简单说来,就是把信号通过激活函数的加工,一层一层的向前“蔓延”,直到抵达输出层。在这里,假设神经元内部的激活函数为Sigmod(f(x)=frac11+e−xf(x)=frac11+e−x)。之所以选用这个激活函数,主要因为它的求导形式非常简洁而优美:
事实上,类似于感知机,每一个神经元的功能都可细分两大部分:(1)汇集各路链接带来的加权信息;(2)加权信息在激活函数的“加工”下,神经元给出相应的输出,如图8-2所示。
图8-2 单个神经元的两部分功能
于是,在正向传播过程中,对于f1(e)f1(e)神经元的更新如图8-3所示,其计算过程如下所示:
图8-3 神经元信息前向更新神经元1的f1(e)
接着,在同一层更新 f2(e)f2(e)的值,过程和计算步骤类似于 f1(e)f1(e),如图8-4所示:
图8-4 神经元信息前向更新神经元2的f2(e)
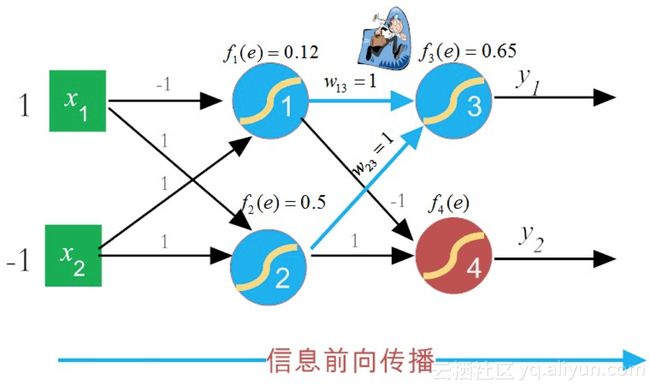
接下来,信息正向传播到下一层(即输出层),更新神经元3的f3(e)f3(e)(即输出y1y1的值),如图8-5所示。
图8-5 神经元信息前向更新神经元3的f3(e)
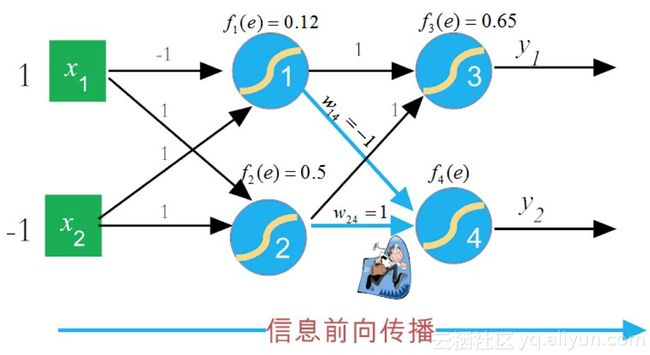
然后,类似地,计算同在输出层求神经元 f4(e)f4(e)(即输出 y2y2)的值,如图8-6所示。
图8-6神经元信息前向更新f4(e)
到此,在第一轮信号前向传播中,实际输出向量已计算得到 y′=[0.65,0.59]Ty′=[0.65,0.59]T,但我们预期输出的向量(即教师信号)是 y=[1,0]Ty=[1,0]T,这二者之间是存在“误差”的。于是,重点来了,下面我们就用“误差”信息反向传播,来逐层调整网络参数。为了提高权值更新效率,这里就要用到下文即将提到的“反向模式微分法则(chain rule)”。
8.2.2 求导中的链式法则
(砰!砰!砰!敲黑板!请注意:如下部分是BP算法最为精妙之处,值得细细品味!)
在前面信号正向传播的示例中,为了方便读者理解,我们把所有的权值都暂时给予了确定之值。而实际上,这些值都是可以调整的,也就是说其实它们都是变量,除掉图8-1中的所有确定的权值,把其视为变量,得就到更为一般化的神经网络示意图8-7。
图8-7 带权重变量的神经网络
这里为了简化理解,我们暂时假设神经元没有激活函数(或称激活函数为y=xy=x),于是对于隐含层神经元,它的输出可分别表示为:
然后,对于输出层神经元有:
于是,损失函数LL可表示为公式(8.2):
这里YY为预期输出值向量(由y1,y2,...,yi,...y1,y2,...,yi,...等元素构成),实际输出向量为fi(w11,w12,...,wij,...,wmn)fi(w11,w12,...,wij,...,wmn)。对于有监督学习而言,在特定训练集合下,输入元素xixi和预期输出yiyi都可视为常量。由此可以看到,损失函数LL,在本质上,就是一个单纯与权值wijwij相关的函数(即使把原本的激活函数作用加上去,除了使得损失函数的形式表现得更加复杂外,并不影响这个结论)。
于是,损失函数LL梯度向量可表示为公式(8.3):
其中,这里的eijeij是正交单位向量。为了求出这个梯度,需要求出损失函数LL对每一个权值wijwij的偏导数。
BP算法之所以经典,部分原因在于,它是求解这类“层层累进”的复合函数偏导数的利器。为啥这么说呢?下面,我们就列举一个更为简化但不失一般性的例子来说明这个观点(以下案例参考了Chris Olah的博客文章[3])。
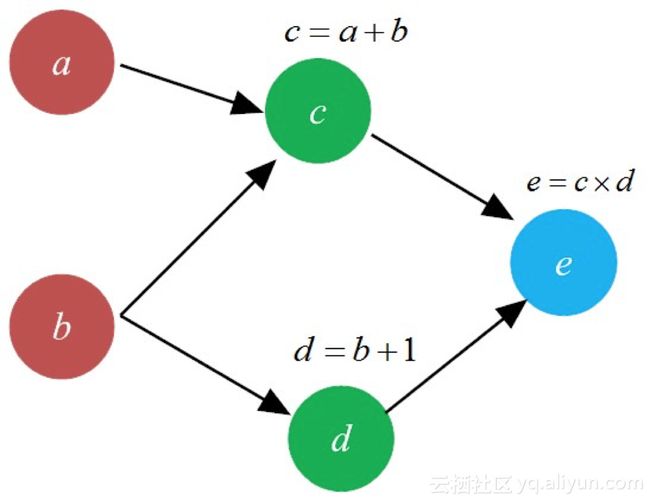
假设有如下一个三层但仅仅包括aa、bb、cc、dd和ee等5个神经元的网络,在传递过程中,cc、dd和ee神经元对输入信号做了简单的加工,如图8-8所示。
图8-8 简易的神经网络
假设变量aa影响cc,此时我们想弄清楚aa是如何影响cc的。于是我们考虑这么一个问题,如果aa变化一点点,那么cc是如何变化的呢?我们把这种影响关系定义为变量cc相对于变量aa的偏导数,记做fracpartialcpartialafracpartialcpartiala。
利用高等数学的知识,我们很容易求得,对于直接相连的神经元(如aa对cc,或bb对dd),可利用“加法规则”或“乘法规则”直接求出。例如,利用加法规则,fracpartialcpartialafracpartialcpartiala可表示为:
而对于表达式为乘法的求偏导规则为:
那么,对于间接相连的神经元,比如aa对ee,如果我们也想知道aa变化一点点时ee变化多少,怎么办呢?也就是说,偏导数fracpartialepartialafracpartialepartiala该如何求呢?这时,我们就需要用到链式法则了。
这里假设a=2a=2,b=1b=1。如果aa的变化速率是1,那么cc的变化速率也是1(因为fracpartialcpartiala=1fracpartialcpartiala=1)。类似地,如果cc的变化速率为1,那么ee的变化速率为2(因为fracpartialepartialc=d=2fracpartialepartialc=d=2)。所以相对于aa变化1,ee的变化为1times2=21times2=2。这个过程就是我们常说的“链式法则”,其更为形式化的表达为(如图8-9所示):
图8-9 链式法则示意图
aa对ee的“影响”属于单路径的影响,还比较容易求得,但这并不是我们关注的重点。因为在神经网络中,神经元对神经元的连接,阡陌纵横,其影响也是通过多条路径“交织”在一起的。在图8-9中,我们研究一下bb对ee的影响,就能比较好理解这一工作机理。显然,bb对ee的影响,也可表达为一个偏导关系:
从图8-9可以看出,bb对ee影响,其实是“兵分两路”:(1)bb通过影响cc,然后通过cc影响ee;(2)bb通过影响dd,然后通过dd影响ee。这就是多维变量(这里“多”仅为2)链式法则的“路径加和”原则。
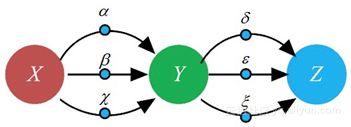
这个原则,看起来简单明了,但其实蕴藏着巨大代价。因为当网络结构庞大时,这样的“路径加和”原则,很容易产生组合爆炸问题。例如,在如图8-10所示的有向图中,如果XX到YY有三条路径(即XX分别以alphaalpha、betabeta和chichi的比率影响YY),YY到ZZ也有三条路径(YY分别以deltadelta、varepsilonvarepsilon和xixi的比率影响ZZ)。
图8-10 路径加和规则演示
于是,很容易根据路径加和原则得到XX对ZZ的偏导数:
上面用到的求偏导数方法,可称之为“前向模式微分(forward-mode differentiation)”,如图8-11-(a)所示。当网络结构简单时,即使XX到ZZ的每一个路径都被“临幸(遍历)”一遍,总共才有 3times3=93times3=9 条路径,但一旦网络结构的复杂度上去了,这种“前向模式微分”,就会让求偏导数的次数和神经元个数的平方成正比。这个计算量,就很可能是成为机器“难以承受的计算之重”。
有道是“东方不亮西方亮”。为了避免这种海量求导模式,数学家们另辟蹊径,提出了一种称之为“反向模式微分(reverse-mode differentiation)”。取代公式(8.4)的那种简易的表达方式,我们用公式(8.5)的表达方式来求XX对ZZ的偏导:
或许你会不屑一顾,这又是在搞什么鬼?把公式(8.4)恒等变换为公式(8.5)又有什么用呢?
图8-11 前向与反向微分方法对比
你可别急,这背后大有玄机,且听我慢慢道来。
前文提到的前向模式微分方法,其实就是我们在高数课堂上学习的求导方式。在这种求导模式中,强调的是某一个输入(比如XX)对某一个节点(如神经元)的影响。因此,在求导过程中,偏导数的分子部分,总是根据不同的节点总是不断变化,而分母则锁定为偏导变量“∂X∂X”,保持定不变(见图8-11-(a))。
相比而言,反向模式微分方法则有很大不同。首先在求导方向上,它是从输出端(output)到输入端进行逐层求导。其次,在求导方法上,它不再是对每一条“路径”加权相乘然后求和,而是针对节点采纳“合并同类路径”和“分阶段求解”的策略。
拿8-11-(b)的例子来说,先求YY节点对ZZ节点的"总影响"(反向第一层):
然后,再求节点XX对节点ZZ的总影响(反向第二层):
特别需要注意的是,fracpartialrmZpartialYfracpartialrmZpartialY已经在第一层求导得到。在第二层仅仅需要求得fracpartialrmYpartialXfracpartialrmYpartialX,而fracpartialrmYpartialXfracpartialrmYpartialX 容易求得(alpha+beta+chi)(alpha+beta+chi),然后二者相乘即可得到所求。这样一来,就大大减轻了第二层的求导负担。在求导形式上,偏导数的分子部分(节点)不变,而分母部分总是随着节点不同而变化,即[fracpartialZpartial][fracpartialZpartial]。
这样说来说去,好像还是不太明白!下面我们还是用图8-9所示的原始例子,对比二者的求导过程,一遍走下来,有了感性认识,你就能明白其中的差异。为了进一步方便读者理解,我们将图8-9重新绘制为图8-12的样子。
图8-12 前向模式微分方法
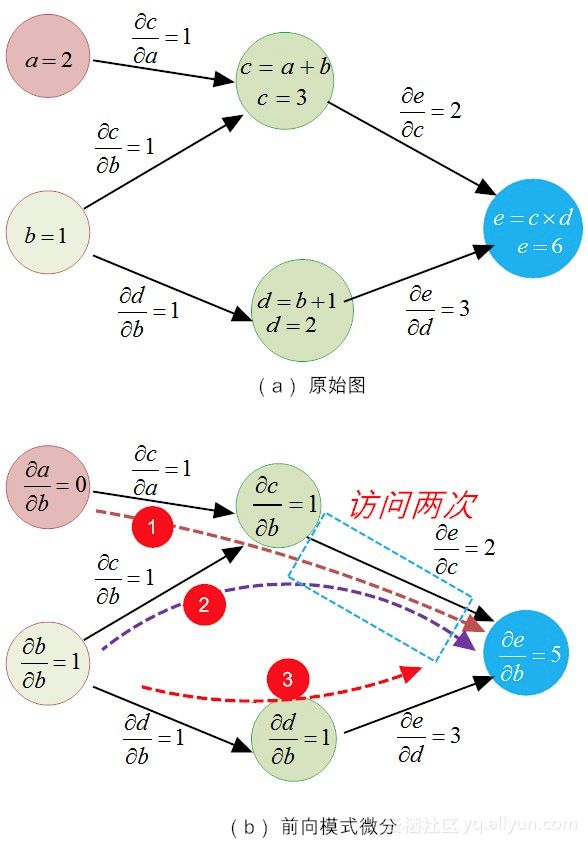
以求变量bb偏导数的流程为例,我们先用前向模式微分法,来说明这种方法的求导过程。根据加法规则,对于求偏导值fracpartialepartialbfracpartialepartialb的步骤可以分两步走:(1)求得所有输入(包括aa和bb)到终点ee的每条路径上的偏导值乘积;(2)对所有条路径的导数值进行加和操作。
从8-12所示的图中,对于两个输入aa和bb,它们共有3条路径抵达终点ee(分别计为①、②和③)。
对于第①条路径而言,输入bb对ee的影响为:
对于第②条路径而言,输入bb对ee的影响为:
对于第③条路径而言,输入bb对ee的影响为:
所以在整体上,输入bb从三条路径上对e施加的“总影响”为:0+2+3=5.
或许读者已经注意到了,有些路径已经被冗余遍历了,比如在图8-12所示中,atoctoeatoctoe(第①条路)和btoctoebtoctoe(第②条路)就都走了路径ctoectoe。
这些局部性的冗余也就罢了,更为“恶劣”的是,对于求fracpartialepartialafracpartialepartiala,上述三条路径,它们同样还得“一个都不能少”地跑一遍,如果求得的变量多了,这到底得有多少冗余啊!
可能你会疑问,对于fracpartialepartialbfracpartialepartialb(fracpartialepartialafracpartialepartiala),第①(③)条路径明明可以不走的嘛?这种明智,是对人的观察而言的,而且是对于简单网络而言的。因为,如果网络及其复杂,人们可能就没有这么“慧眼识珠”,识别其中的路径冗余。
此外,对于计算机而言,有些时候,局部操作的“优化”,相对于整体操作的“规范化”,顶多算得上“奇淫巧技”,其优势可谓是“荡然无存”。有过大规模并行编程经验的读者,可能对这个观点会有更深的认知。
然而,同样是利用链式法则,反向模式微分方法就能非常机智地避开了这种冗余(下面即将讲到的BP算法,正是由于这么干,才有其优势的)。在这种方法中,它能做到对每一条路径只“临幸”一次,这是何等的节俭!下面我们来看看它是如何工作的。
图8-13反向模式微分方法
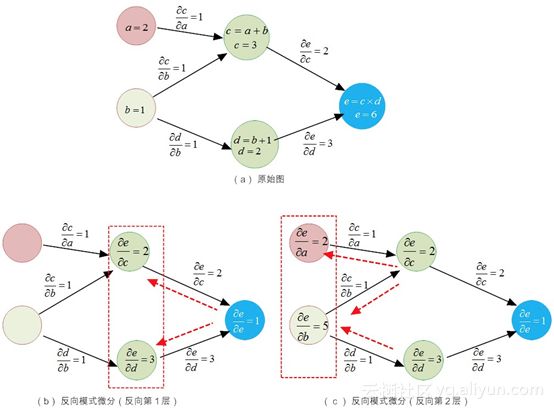
相比于“前向模式微分法”是以输入(如图8-13-(a)所示的aa和bb)为锚点,正向遍历每一条可能的路径。反向模式微分法是以节点(或说神经元,如图8-13-(a)所示的ee、cc和dd)为锚点,逐层分阶段求导,然后汇集每一个节点的外部路径(合并同类路径)。
如图8-13-(b)所示,在反向求导的第1层,对于节点cc有:
类似的,对于节点dd有:
在阶段性的求解完毕第一层的导数之后,下面开始求解第二层神经元变量的偏导。如图8-13-(c)所示,在反向第2层,对于节点aa有如图8-14-(Ⅰ)所示的求导模式。
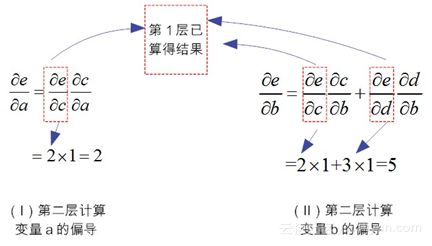
图8-14反向模式微分方法的推演
特别需要注意的是,8-14-(Ⅰ)所示的表达式“fracpartialepartialcfracpartialcpartialafracpartialepartialcfracpartialcpartiala”中左部“fracpartialepartialcfracpartialepartialc”,已经在第1层求解过了,并“存储”在神经元cc中。此时,采用“拿来主义”,拿来就能用!这就是反向模式微分的精华所在!
类似地,在反向求导第2层,对于节点bb,由于它汇集“两路兵马”的影响,所以需要合并同类路径,有如图8-14-(Ⅱ)所示结果。
这样一来,如图8-13反向模式微分方法,每个路径仅仅遍历一次,就可以求得所有输出(如ee节点)对输入(如aa或bb节点)的偏导,干净利落,没有任何冗余!
在第七章中,我们曾提到,“BP算法把网络权值纠错的运算量,从原来的与神经元数目的平方成正比,下降到只和神经元数目本身成正比。”其功劳,正是得益于这个反向模式微分方法节省的计算冗余
8.2.3 误差反向传播
有了前面“链式求导”的知识铺垫,下面我们就来细细讲解误差反向传播的过程。鉴于我们的系列文章是写给初学者(实践者)看的,下面我们尽量省略了其中较为复杂的推导公式,对该部分感兴趣的读者可参阅卡内基梅隆大学Tom Mitchell教授的经典著作《机器学习》[3](对公式不感冒的读者,第一遍阅读可以直接跳过公式,直达图文解释部分)。
误差反向传播通过梯度下降算法,迭代处理训练集合中的样例,一次处理一个样例。对于样例dd,如果它的预期输出(即教师信号)和实际输出有“误差”,BP算法抓住这个误差信号LdLd,以“梯度递减”的模式修改权值。也就是说,对于每个训练样例dd,权值wjiwji的校正幅度为DeltawjiDeltawji(需要说明的是,wjiwji和wijwij其实都是同一个权值,wjiwji表示的是神经元jj的第ii个输入相关的权值,这里之所以把下标“jj”置于“ii”之前,仅仅表示这是一个反向更新过程而已):
在这里,LdLd表示的是训练集合中样例dd的误差,分解到输出层的所有输出向量,LdLd可表示为:
其中:
yjyj表示的是第jj个神经单元的预期输出值。
y′jyj′表示的jj个神经单元的实际输出值。
outputsoutputs的范围是网络最后一层的神经元集合。
下面我们推导出fracpartialLdpartialwjifracpartialLdpartialwji的一个表达式,以便在公式(8.7)中使用梯度下降规则。首先,我们注意到,权值wjiwji仅仅能通过netjnetj影响其他相连的神经元。因此利用链式法则有:
在这里,netj=sumnolimitsiwjixjinetj=sumnolimitsiwjixji,也就是神经元jj输入的加权和。xjixji表示的神经jj的第ii个输入。需要注意的是,这里的xjixji是个统称,实际上,在反向传播过程中,在经历输出层、隐含层和输入层时,它的标记可能有所不同。
由于在输出层和隐含层的神经元对“纠偏”工作,承担的“责任”是不同的,至少是形式不同,所以需要我们分别给出推导。
(1)在输出层,对第ii个神经元而言,省略部分推导过程,公式(8.8)的左侧第一项为:
为了方便表达,我们用该神经元的纠偏“责任(responsibility)”delta(1)jdeltaj(1)描述这个偏导,即:
这里delta(1)jdeltaj(1)的上标“(1)”,表示的是第1类(即输出层)神经元的责任。如果上标为“(2)”,则表示第2类(即隐含层)神经元的责任,见下面的描述。
(2)对隐含层神经元jj的梯度法则(省略了部分推导过程),有:
其中:
fjfj表示神经单元jj的计算输出。
netjnetj表示的是神经单元jj的加权之和。
Downstream(j)Downstream(j)表示的是在网络中神经单元jj的直接下游单元集合。
隐含层神经元的纠差职责,是通过计算前一步输出神经元的“责任”来实现的。
这里说的每层神经元“责任”,或者更为确切来说是“纠偏责任”,其实就是在8.2.2节讲到的“分阶段求解”策略。
在明确了各个神经元“纠偏”的职责之后,下面就可以依据类似于感知机学习,通过如下加法法则更新权值:
对于输出层神经元有:
对于隐含层神经元有:
在这里,etain(0,1)etain(0,1)表示学习率。在实际操作过程中,为了防止错过极值,etaeta通常取小于0.1的值。hjhj为神经元j的输出。xjkxjk表示的是神经单元jj的第kk个输入。
上面的公式依然比较抽象,难以理解。下面我们还是以前面的神经网络拓扑结构为例,用实际运算过程给予详细说明,以期望给与读者感性认识。
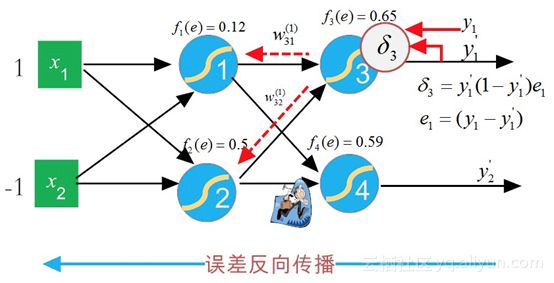
从上面的描述可以得知,针对输出层的神经元3,它的输出值y′1y1′为0.65,而期望输出值y1y1为1,二者存在“误差”:e1=y1−y′1=1−0.65=0.35e1=y1−y1′=1−0.65=0.35。
在这里,我们把每个神经元根据误差调参的“责任”记为deltadelta,那么,根据公式(8.9)和(8.10),神经元3的“责任”可表示为:
图8-15 误差反向传播计算神经元3的“责任”
从上面分析可知,我们很容易计算出delta(1)3delta3(1)的值:
于是,可以反向更新w(1)31w31(1)的权值为:
在这里,![]() (具体推导见公式8.8-8.10),etaeta为学习率,此处取值为0.1。f1f1为神经元1的输出(即y′1y1′)。
(具体推导见公式8.8-8.10),etaeta为学习率,此处取值为0.1。f1f1为神经元1的输出(即y′1y1′)。
类似地,我们可以反向更新w(1)32w32(1))的权值: