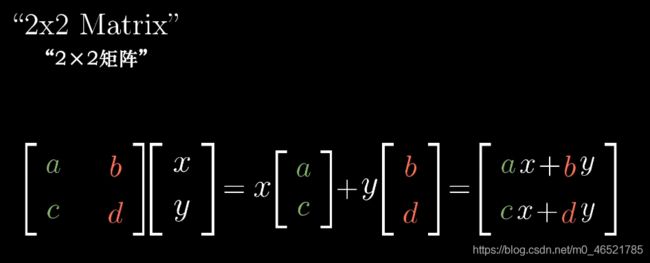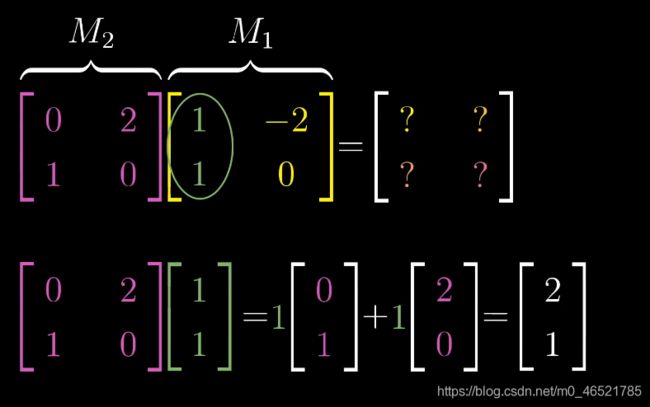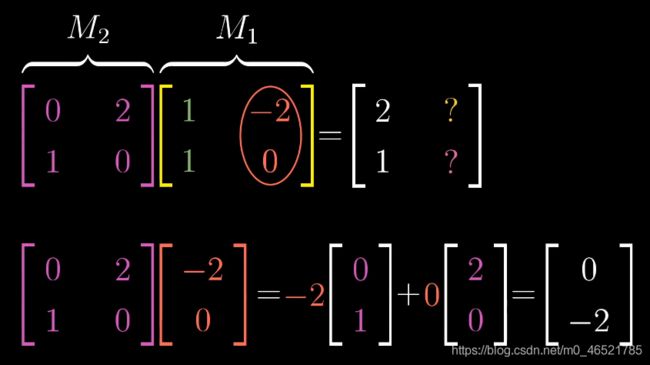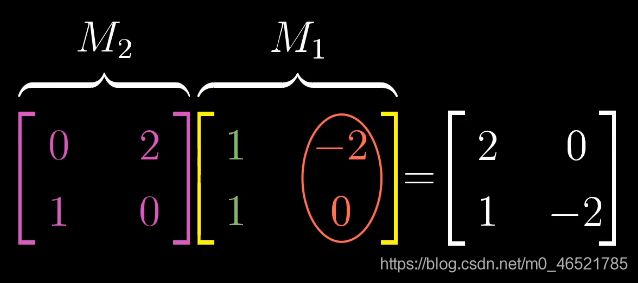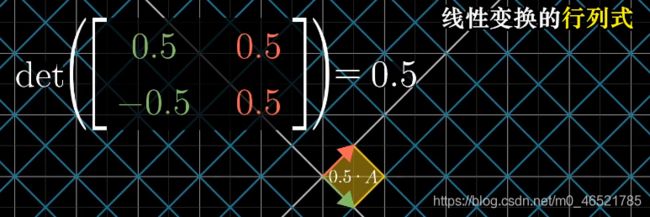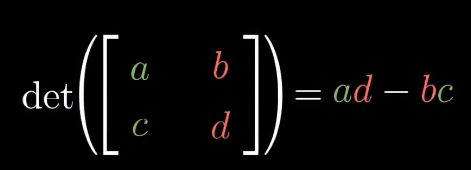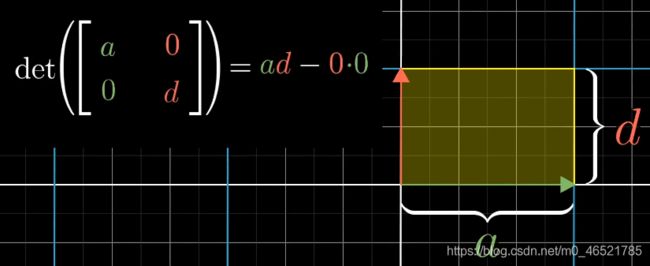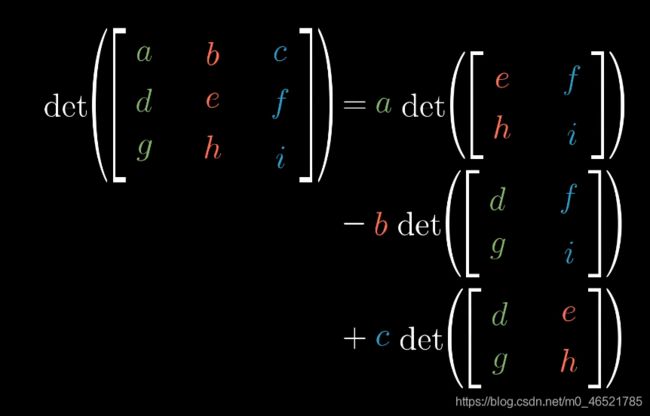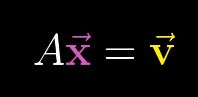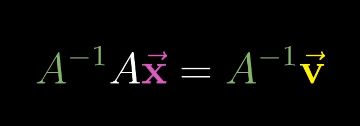线性代数的实质

矩阵与线性变换

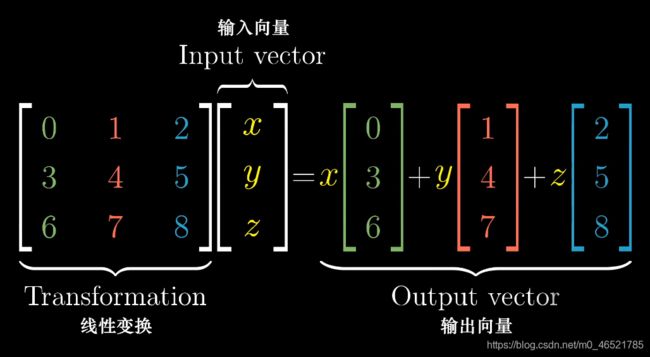
矩阵可以看成空间两条向量组成的[a,c],[b,d]，即平面的一条基向量，我们计算乘法的时候，只需要计算x[a,c],y[b,d]即可，即前取行。后取列，然后相加。

我们可以把矩阵的列看作变换之后的基向量，矩阵乘法看成他们的线性组合。真是太有意思了

｀当只进行一次变换的时候，即第二个矩阵只有一列，这个计算方式更简单。｀

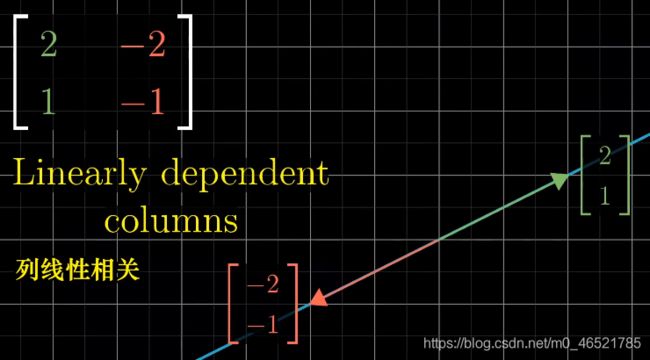
因此，当有两列成倍数的时候，两个基向量就在同一条直线上了

如果理解了矩阵乘法就是空间变换，后面的概念就很好理解了

#　矩阵乘法与线性变换

我们需要时刻牢记，两个矩阵相乘有着几何意义，也就是两个线性变换的相继作用。如下，两步可以合成一步，分步骤就是两步，只看结果就是一步，这是等价的。

但是等价过程的运算是什么样的呢？这就是我们说的矩阵乘法了。

矩阵乘法怎么计算呢？就和乘法分配律类似，我们只需要找到ｉ和ｊ的去向即可，步骤如下：

①首先从右看，找到第一列，来观察ｉ的去向（古人习惯ｆ（ｇ（ｘ）的表达，所以从右往左看）

②观察ｊ的去向

③于是得到最后的结果

当然，不排除，前取行，后取列这个公式有时候计算更加简单，但对其运算的实质却什么都体现不出来。

同时，我们这样算就省去了繁琐的加法，直接对应，然后拼在一起就好，其实这个最后就得到了前取行，后取列的公式

但是，当只进行一次变换的时候，即第二个矩阵只有一列，这个计算方式更简单。

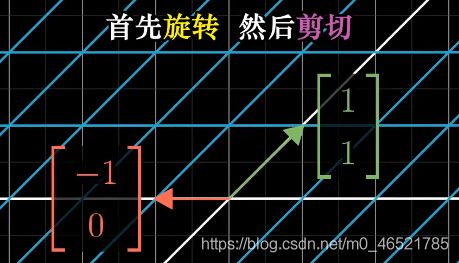
这样，我们就可以很轻易的解释为什么不符合交换律了，因为先剪切，后旋转得到的图形，和原图形完全不符。

虽然矩阵乘法不满足交换律，但是满足分配律，我们只要满足一个方向即可，几何变换很好解释这一说法

三维空间中的线性变换

这是旋转的

计算方法和二维相同

行列式

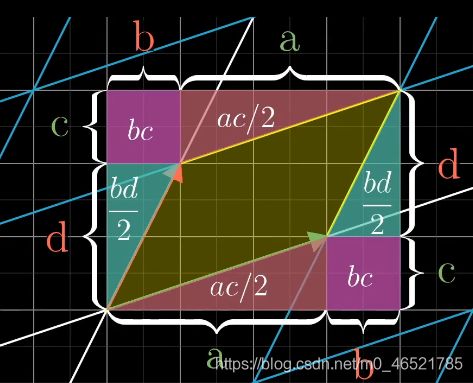
我们讲基向量进行拉伸，旋转之后，原来坐标系的图形面积大小就会发生相应变化，变化的倍数就叫行列式。

如果得到负值，就相当于把平面反转了，本来ｉ是ｘ轴，ｊ是ｙ轴，现在变成了，ｊ是ｘ轴，ｉ是ｙ轴了。

那怎么计算呢？

那为什么是这样计算的呢？

我们假设ｂ和ｄ都是０（没有旋转），因此，ｉ拉伸了ａ倍，ｊ拉伸了ｄ倍

这个简图可以为一般情况提供参考

这里是三维的计算公式

矩阵乘法之后，得到的矩阵的行列式，与两个行列式直接做乘法的结果相同，证明类似二维的。

矩阵与线性方程组

逆矩阵

Ａ的逆，与Ａ做矩阵乘法，会回到最初的状态，即什么都没做，这个什么都没做的变换称为恒等变换

我们可以通过两边同乘一个Ａ的逆，来求解向量方程

秩

“秩”代表着变化后空间的维数，准确点说是列空间的维数，当秩达到最大值得时候，意味着秩和列数相等，我们称为满秩

列空间

列空间就是矩阵的列所张成的空间。

零向量一定会被包含在列空间里，因为线性变换的基础是原点不变呀

零空间

变换后落在原点的向量的集合，被称为矩阵的“零空间”或“核”

向量的点积

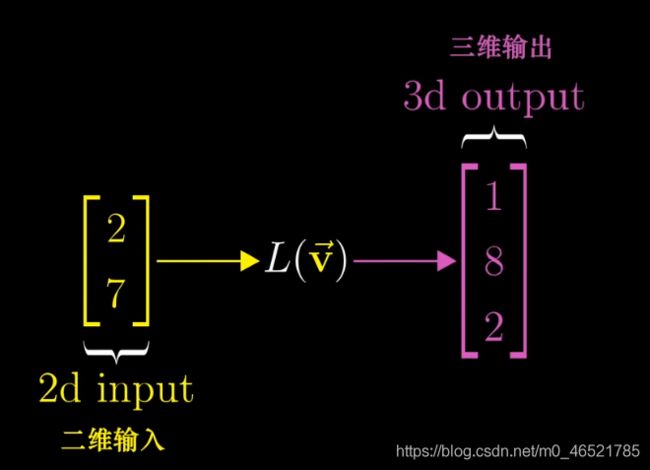
非方阵

这个是两列三行，表示有两个基向量，每个是三维的

这个表示有三个向量，每个向量有两个维度