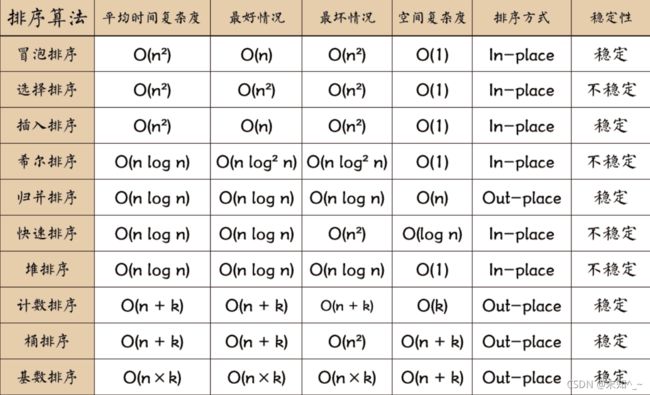
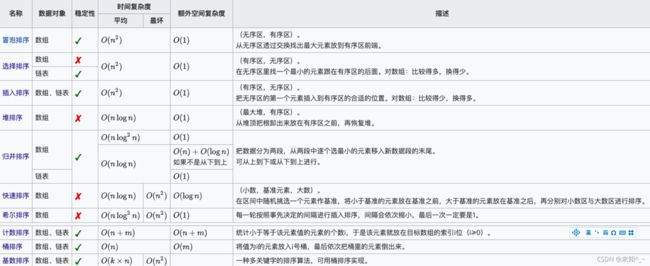
十一种排序算法(图解+代码+秋招面试遇到的分析)。
排序算法
-
-
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 桶排序
- 基数排序
- 位图排序
- 布隆过滤器
- 快速幂
-
秋招时遇到的:
- 快速排序思路
- 大数据量排序–使用bitmap排序
菜鸟教程
Acwing
冒泡排序
void bubble_sort(T arr[], int len){
for(int i = 0; i < len - 1; i ++){
for(int j = 0; j < len - 1 - i; j ++){
if(arr[j] > arr[j + 1]){
swap(arr[j], arr[j + 1]);
}
}
}
}
选择排序
void selection_sort(vector<T>& arr){
for(int i = 0; i < arr.size() -1; i ++){
int min = i;
for(int j = i + 1; j < arr.size(); i ++){
if(arr[j] < min) min = j;
}
swap(arr[j], arr[min]);
}
}
插入排序
有直接插入排序和折半插入排序两种
void insertion_sort(int arr[], int len){
for(int i = 1; i < len; i++){
int key = arr[i];
int j = i - 1;
while((j >= 0) && (key < arr[j])){
arr[j + 1] = arr[j];
j --;
}
arr[j + 1] = key;
}
}
希尔排序
思想:设计一个增量序列,最后一次一定是1
每趟排序,把待排序记录分成若干子序列,分别插入排序
void shell_sort(T array[], int length){
int h = 1;
while(h < length / 3){
h = 3 * h + 1;
}
while(h >= 1){
for(int i = h; i < length; i++){
for(int j = i; j >= h && array[j] < array[j - h]; j -= h){
swap(array[j], array[j - h]);
}
}
h = h / 3;
}
}
归并排序
void merge_sort(int q[], int l, int r){
if(l >= r) return;
int mid = l + r >> 1;
merge_sort(q, l, mid);
merge_sort(q, mid + 1, r);
int k = 0, i = 1, j = mid + 1;
while(i <= mid && j <= r)
if(q[i] <= q[j]) tmp[k ++] = q[i ++];
else tmp[k ++] = q[j ++];
while(i <= mid) tmp[k ++] = q[i ++];
while(j <= r) tmp[k ++] = q[j ++];
for(i = l, j = 0,i <= r; i++, j ++) q[i] = tmp[j];
}
快速排序
void quick_sort(int q[], int l, int r){
if(l >= r) return;
int i = l -1, j = r + 1, x = q[l + r >>1];
while(i < j){
do i ++; while(q[i] < x);
do j --; while(q[j] > x);
if(i < j) swap(q[i], q[j]);
}
quick_sort(q, l, j), quick_sort(q, j+ 1, r);
}
堆排序
思想:大根堆
//将以k为根结点的树调整为大根堆
void HeadAdjust(int a[], int k, int len){
//注:除k结点外其他已经有序
a[0] = a[k];//a[0]暂存子树根节点
for(int i = 2 * k; i <= len; i *= 2){
//沿较大子结点筛选
if(i < len && a[i] < a[i + 1]) i ++;//i为较大子结点下标 (i
if(a[0] >= a[i]) break;//筛选结束
else{
a[k] = a[i];//递归处理子结点
k = i;
}
}
a[k] = a[0];
}
//建大根堆 时间复杂度---O(n)
void BuildHeap(int a[], int len){
//从下往上建堆,从最后一个叶子结点的根节点开始
for(int i = len / 2; i > 0; i --){
//处理所有非终端结点
HeadAdjust(a, i , len);
}
}//建堆过程关键字的比较次数不超过4n(定理)
//堆排序的完整逻辑
void HeapSort(int a[], int len){
BuildHeap(a, len);//建堆 O(n)
for(int i = len; i > 1; i --){
//从后往前处理 ,共n-1趟交换和调整
swap(a[i], a[1]);//将堆顶元素(最大元素)与堆底元素交换
HeadAdjust(a, 1, i - 1);//把剩余待排元素调整为堆
}
}//每趟时间复杂度不超过o(h) = O(logn),共 n-1趟
计数排序
思想:每个桶只存储一个单一的值
朴素版 根据最大值开辟存储空间且不稳定
void count_sort(int a[], int n){
int minval = a[0], maxval = a[0];
for(int i = 0; i < n; i++){
minval = min(minval, a[i]);
maxval = max(maxval, a[i]);
}
int cnt[maxval + 1] = {
0};
for(int i = 0; i < n; i ++) cnt[a[i]] ++;
for(int i = minval, k = 0; i <= maxval; i++){
while(cnt[i] != 0){
data[k ++] = i;
cnt[i] --;
}
}
}
优化版 根据实际的数组长度开辟空间且不稳定
void count_sort(int a[], int n){
int minval = a[0], maxval = a[0];
for(int i = 0; i < n; i++){
minval = min(minval, a[i]);
maxval = max(maxval, a[i]);
}
int d = maxval - minval + 1;
int cnt[d] = {
0};
for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;
for(int i = 0, k = 0; i <= maxval - minval; i++){
while(cnt[i] != 0){
data[k ++] = i + minval;
cnt[i] --;
}
}
}
二次优化版 稳定排序
//二次优化
void count_sort(int a[], int n){
//遍历数组求得最大值和最小值
int minval = a[0], maxval = a[0];
for(int i = 0; i < n; i ++){
minval = min(minval, a[i]);
maxval = max(maxval, a[i]);
}
int d = maxval - minval + 1;// 计数数组的实际长度
int cnt[d] = {
0};//根据最大值开辟新数组空间
//统计原数组中元素出现的次数
for(int i = 0; i < n; i ++) cnt[a[i] - minval] ++;//将元素映射到a[0...d-1]
int sum = 0;
for(int i = 0; i < d; i ++){
//本质为前缀和数组,用于求位次
sum += cnt[i];//此处的cnt既为元素又为之前的元素和,即cnt[i] = cnt[i] + cnt[i - 1]
cnt[i] = sum;// 比如, cnt[5] = 3,表示分数95, 排名第 3
}
int sortArray[d];//sortArray[]存元素真实序列
for(int i = n - 1; i >= 0; i --){
//将原数组元素从后往前遍历
sortArray[cnt[a[i] - minval] - 1] = a[i];
cnt[a[i] - minval] --;
}
//将排序后的序列赋给原数组
for(int i = 0, k = 0; i < d; i ++){
data[k ++] = sortArray[i];
}
}
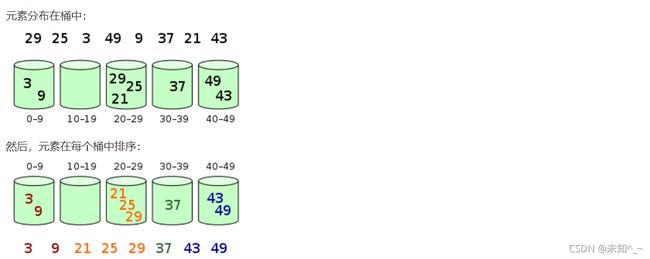
桶排序
空间换时间
思想:把一个范围的数值分到一个桶
void bucket_sort(int a[], int n){
int minval = a[0], maxval = a[0];
for(int i = 0; i < n; i++){
minval = min(minval, a[i]);
maxval = max(maxval, a[i]);
}
int bnum = 10;//桶中的元素的个数
int m = (maxval - minval) / bnum + 1;
vector< vector<int>> bucket(m);
for(int i = 0; i < n; i++) bucket[(a[i] - minval ) / bnum].push_back(a[i]);
for(int i = 0; i < m; i++) sort(bucket.begin(), bucket.end());
for(int i =0, k = 0; i < m; i++){
for(int j = 0; j < bucket[i].size();j ++){
data[k ++] = bucket[i][j];
}
}
}
基数排序
思想:把每一位的数字分到一个桶中
int maxbit(int data[], int n) //辅助函数,求数据的最大位数
{
int maxData = data[0]; ///< 最大数
/// 先求出最大数,再求其位数,这样有原先依次每个数判断其位数,稍微优化点。
for (int i = 1; i < n; ++i)
{
if (maxData < data[i])
maxData = data[i];
}
int d = 1;
int p = 10;
while (maxData >= p)
{
//p *= 10; // Maybe overflow
maxData /= 10;
++d;
}
return d;
/* int d = 1; //保存最大的位数
int p = 10;
for(int i = 0; i < n; ++i)
{
while(data[i] >= p)
{
p *= 10;
++d;
}
}
return d;*/
}
void radixsort(int data[], int n) //基数排序
{
int d = maxbit(data, n);
int *tmp = new int[n];
int *count = new int[10]; //计数器
int i, j, k;
int radix = 1;
for(i = 1; i <= d; i++) //进行d次排序
{
for(j = 0; j < 10; j++)
count[j] = 0; //每次分配前清空计数器
for(j = 0; j < n; j++)
{
k = (data[j] / radix) % 10; //统计每个桶中的记录数
count[k]++;
}
for(j = 1; j < 10; j++)
count[j] = count[j - 1] + count[j]; //将tmp中的位置依次分配给每个桶
for(j = n - 1; j >= 0; j--) //将所有桶中记录依次收集到tmp中
{
k = (data[j] / radix) % 10;
tmp[count[k] - 1] = data[j];
count[k]--;
}
for(j = 0; j < n; j++) //将临时数组的内容复制到data中
data[j] = tmp[j];
radix = radix * 10;
}
delete []tmp;
delete []count;
}
位图排序
思想:用对应的32bit位对应十进制的0-31个数
位移转换:
1.确定十进制数在数组中下标的位置 idx = b[i] / 32;
2.求十进制数对应0-31中的数 x = b[i] % 32;
3.利用位移操作 b[idx] += (1 << 1);
@Test
public void bitmap_sort()
{
int[] a = new int[]{
1, 6, 22, 4, 7, 2, 8, 30, 25, 5, 67, 80, 54, 90, 142};
int[] b = new int[1 + 142/ 32];
for (int k : a) {
int idx = k / 32;
int x = k % 32;
b[idx] += 1 << x;
}
for(int j = 0; j < b.length; j++){
for(int i = 0; i < 32; i ++){
if((b[j] >> i & 1) == 1) System.out.print(32 * j + i + " ");
}
}
}
布隆过滤器
可以解决缓存击穿的问题
本质上布隆过滤器是一种数据结构,比较巧妙的概率型数据结构(probabilistic data structure),特点是高效地插入和查询,可以用来告诉你 “某样东西一定不存在或者可能存在”。
参考知乎
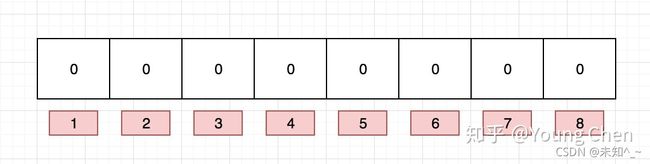
布隆过滤器是一个 bit 向量或者说 bit 数组,长这样:
如果我们要映射一个值到布隆过滤器中,我们需要使用多个不同的哈希函数生成**多个哈希值,**并对每个生成的哈希值指向的 bit 位置 1,例如针对值 “baidu” 和三个不同的哈希函数分别生成了哈希值 1、4、7,则上图转变为:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Bmb2hSPx-1637905762214)(C:\Users\Keqiang.Wang1\Desktop\新建文件夹\images\布隆过滤器2.jpg)]
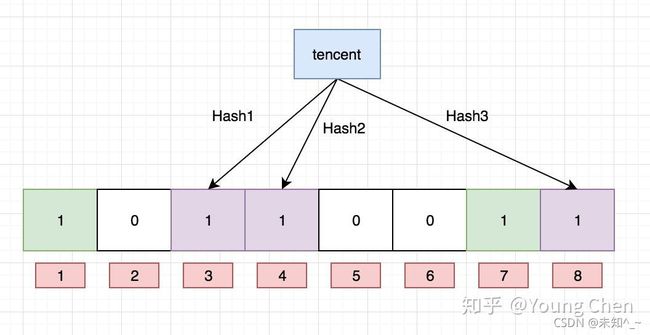
Ok,我们现在再存一个值 “tencent”,如果哈希函数返回 3、4、8 的话,图继续变为:
值得注意的是,4 这个 bit 位由于两个值的哈希函数都返回了这个 bit 位,因此它被覆盖了。现在我们如果想查询 “dianping” 这个值是否存在,哈希函数返回了 1、5、8三个值,结果我们发现 5 这个 bit 位上的值为 0,说明没有任何一个值映射到这个 bit 位上,因此我们可以很确定地说 “dianping” 这个值不存在。而当我们需要查询 “baidu” 这个值是否存在的话,那么哈希函数必然会返回 1、4、7,然后我们检查发现这三个 bit 位上的值均为 1,那么我们可以说 “baidu” 存在了么?答案是不可以,只能是 “baidu” 这个值可能存在。
这是为什么呢?答案跟简单,因为随着增加的值越来越多,被置为 1 的 bit 位也会越来越多,这样某个值 “taobao” 即使没有被存储过,但是万一哈希函数返回的三个 bit 位都被其他值置位了 1 ,那么程序还是会判断 “taobao” 这个值存在。
传统的布隆过滤器并不支持删除操作。但是名为 Counting Bloom filter 的变种可以用来测试元素计数个数是否绝对小于某个阈值,它支持元素删除。
快速幂
m^k%p
思想:把k分成 2^0 + 2^1 + …
int qmi(int m, int k, int p){
int res = 1 % p;
while(k){
if(k&1) res = res * m % p;
m = m * m % p;
k >> 1;
}
return res;
}