Gradient Descen-multivariate(吴恩达机器学习:梯度下降在线性模型的应用)
梯度下降算法在Linear Regression中的应用
文章目录
- 梯度下降算法在Linear Regression中的应用
-
- 多变量(multivariate)
-
- 题目:预测房价
- 数据标准化
- 处理Training set
- 输入输出的数据提取并转换成矩阵形式
- 损失函数求解
- 梯度下降算法
- 可视化
- 预测
数据处理过程和单变量类似,原理部分不再赘述。
多变量(multivariate)
题目:预测房价
输入:房屋大小、卧室数量
输出:房价
第一列为房屋大小,第二列为卧室数量,前两列为输入
第三列为房价,即理想输出
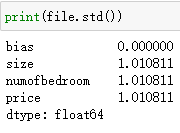
数据标准化
![]()
在输入X中,房屋大小和卧室数量之间差距过大;在输出y中,房屋价格和卧室数量之间的差距也很大,会影响梯度下降中的收敛速度,所以需要对数据进行标准化,即把每一列都变成均值为0,标准差为1的数据。代码如下:
file = pd.read_csv('E:/吴恩达机器学习/machine-learning-ex1/ex1/ex1data2.txt', header=None, names=['size', 'numofbedroom', 'price'])
file = (file-file.mean())/np.std(file)
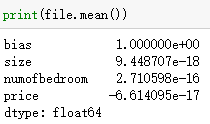
记录一些数据,之后会用到。
file_size_mean = file.mean()['size']
file_size_std = file.std()['size']
file_bedroom_mean = file.mean()['numofbedroom']
file_bedroom_std = file.std()['numofbedroom']
file_price_mean = file.mean()['price']
file_price_std = file.std()['price']
file = (file-file.mean())/np.std(file)
注意:这里file中的每一列减去的是每一列各自的均值,并不是整体的均值。
处理Training set
file.insert(0, 'bias', 1)
由于不再是单数入,这里不再对training set进行可视化。
输入输出的数据提取并转换成矩阵形式
""" 获取所需数据并转化为矩阵 """
X = file.iloc[:, 0:3] # 参数权重theta
y = file.iloc[:, 3:] # 理想输出y
X = np.matrix(X, dtype='float64')
y = np.matrix(y, dtype='float64')
m = len(y)
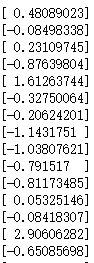
X的维数为(97, 3),y的维数为(97, 1),X中有插入的一列全1列。部分X数据和y数据如下:
输入X(含一列全1列)

损失函数求解
首先定义权重theta、学习率alpha、迭代次数iterations
alpha = 0.31
num_iters = 50
theta = np.array([[0.01],[0.02],[0.03]])
theta定义为 (3, 1)的数组,这里把theta设置成不同的值,防止在梯度下降中权重值始终相同。
以下是损失函数CostFunctionx向量求解代码:

def computeCostMulti(X, y, theta):
cost_temp = (X*theta-y).transpose()*(X*theta-y)
return cost_temp/(2*m)
向量方式求解代价函数较为方便,这里不再做过多讲解,类似原理参见单变量博客。
在初始权重theta的时候,我们调用损失函数查看运行结果:
J_theta = computeCostMulti(X, y, theta) # 计算代价函数
运行结果:
梯度下降算法
![]()
注意,梯度下降是不断更新权重theta,并不是更新X或y,之后权重会影响模型的预测效果,而与输入输出无关。
对每一个权重theta,更新时刻为累加完所有的m个代数值后,所得累加值在与学习率alpha和样本数据m进行运算后才进行theta更新。
# 梯度下降
def gradientDescentMulti(X, y, theta, alpha, num_iters):
J_history = np.zeros((num_iters, 1))
for iter in range(num_iters):
diff = X*theta - y
gradient_cost = (1/m) * (X.transpose()*diff)
theta = theta - alpha*gradient_cost
J_history[iter] = computeCostMulti(X, y, theta)
return theta, J_history
theta, J_history = gradientDescentMulti(X, y, theta, alpha, num_iters)
定义了一个记录每次更新权重完成后损失函数值的变量J_history,可以在迭代完成后可视化梯度下降的效果,在每一次更新theta值之后,用新的theta值计算代价函数并存放在J_history中。
diff为 ( h_theta(x) - y ),为(m, 1)维。其中的每一行都是某一训练集样本中预测输出与实际输出的差值。
在算法公式中,每一个权重theta_j最后对应需要乘一个X_j,而X是(m,3)维,每一列是一个X_j在不同训练集样本输入下的列向量;每一行为一个训练集样本。所以可以考虑把X转置,之后再与diff进行矩阵相乘,所得结果为(3, 1)矩阵,其中的值等于对应的theta的算法中的求和部分。求出的结果再与alpha和m进行运算,得到theta的更新部分。
可视化
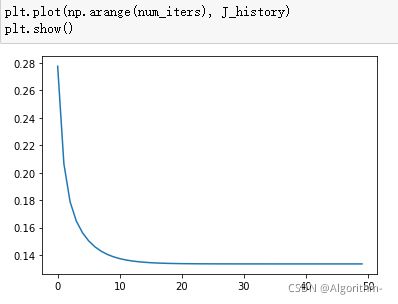
该部分要绘制代价函数随迭代次数而变化的曲线。代码如下:
plt.plot(np.arange(num_iters), J_history)
plt.show()
预测
def pridicit(size, numofbedroom):
X = np.matrix([1, (size-file_size_mean)/file_size_std, (numofbedroom-file_bedroom_mean)/file_bedroom_std], dtype='float64')
return ((X * theta)*file_price_std + file_price_mean)
传入参数:房屋大小和卧室数量。
输出:房价。
注意:传入的输入参数需要经过标准化过程,而输出的参数需要经过逆标准化过程得出实际房屋价格值。
price = pridicit(2000, 3)
print(price)
单变量部分的博客链接点击这里。
NG Machine Learning Courses
链接:https://pan.baidu.com/s/1FoAQNRdevsqYzW4a5QDsBw
提取码:0wdr